Kraft – die neusten Beiträge

Guten Abend,

leider verstehe ich die Aufgabe noch nicht so wirklich… Wieso sind hier in der Lösung zwei Kreise eingezeichnet? Der Radius der Kreisbahn (Teilaufgabe a)) müsste doch von dem Massenschwerpunkt der Kugel bis zum Massenschwerpunkt des Menschen sein. Wieso ist dann der Radius der Kreisbahn nicht 1,8 m, sondern 1,7 m?

Muss der Kraftarm an der Schere z.B immer größer als det Lastarm sein?

Ich habe eine zeichnung von einer Schere gemacht aber habe ausversehen Kraftarm kleiner gemacht ist das schlimm?

Danke!

kann man irgendwie die Elemente kontrolieren? was mir an mir aufgefallen ist das ich immer wenn ich mich Pflanzen näher komme spüre ich so ein kribbeln . Und ich fühle mich schon immer mit dem Wasser verbunden.Feuer finde ich unglaublig fastzinierent.Und ich liebe denn Wind und fühle mich so frei wenn er ihn mein gesicht bläst.(sorry für die Rechtschreibung)ES IST KEINE EINBILDUNG!

"Die Länge der Beschleunigungsstrecke betrug 7000 m.

Der Schlitten erreichte nach konstanter Beschleunigung eine Geschwindigkeit von 2972 km/h. Berechnen Sie die Dauer der Fahrt und die Beschleunigung des Raketenschlittens."

Ich verstehe das überhaupt nicht, und ich bin mir nicht sicher, was ich tun soll :( Kann mir jemand helfen? Es handelt sich nicht um Hausaufgaben, sondern um Übung für eine Prüfung

Was denkt ihr? So im Vergleich zu den durchschnittlich starken mann oder der durchschnittlich starken Frau. Macht ihr Sport der euch stärkt wenn ja welchen?

Ich bräuchte Hilfe bei dieser Aufgabe. Am besten einen ausführlichen Rechenweg. Vielen Dank für die Hilfe im Voraus.

A: Ein Ball soll von 2 m über dem Boden über eine 10 m hohe und 2 m entfernte Mauer geschossen werden. Dabei kann der Abwurfwinkel Alpha gegen die Horizontale kontinuierlich von 0 (waagerecht) bis 90 (senkrecht) eingestelt werden. Die Abschussgeschwindigkeit ist fest auf den Betragd Vo = 20 m/s eingestellt.

Für welche Werte von Alpha kann der Ball über die Mauer geschossen werden?

Bevor ihr mich falsch versteht:

Ich verstehe, das Gravitation keine wirkliche Kraft ist und das sie durch die Krümmung der Raum-Zeit entsteht.

Wenn wir jetzt eine gekrümmte Raumzeit haben, ziehen sich die Objekte ja an. Sie bewegen sich auf der gekrümmten Bahn. Aber warum können die Objekte nicht anhalten, sondern sie fallen einfach in diesen Gravitationstrichter? Woher kommt es das die in den Gravitationstrichter fallen?

Wenn ich eine Feder und einen Stein im Vakuum fallen lasse, warum werden sie gleich beschleunigt??

Ich will jetzt keine Antwort haben wie "Ist so, wegen der Schwerkraft", ich hätte gerne eine Wissenschaftlich korrekte Antwort.

Danke

Wir gucken mal auf meine wunderbare Abbildung. Abbildung 1 Zeigt eine seitlich liegende Wasserflasche in einem Auto was beschleunigt. Wenn das Auto beschleunigt, wird das Wasser der Flasche ja entgegen der Beschleunigung "nach hinten" gedrückt denn es wird ja nach vorne beschleunigt.

Wenn wir jetzt die Wasserflasche auf die Erde stellen, wird das Wasser ja auch nach unten gezogen, heißt es also wir beschleunigen die ganze Zeit nach oben? Eigentlich müsste es ja sein, denn im Auto bewegt sich das Wasser ja auch entgegengesetzt der Beschleunigung.

Warum ist das so?

Wirkt Gravitation nach oben?

Hallo.

Wenn ich eine Feder habe, die z. B. 15 cm lang ist, könnte man diese auch um das 3 fache oder mehr dehnen, solange es die Belastbarkeit zulässt?

Ich kann mir das irgendwie schlecht vorstellen.

mal Angenommen man trägt auf einer Treppe einen Schrank hoch mit 2 Personen wo müsste man den Schrank tragen damit er am leichtesten ist

Ich habe im Studium diese Aufgabe bekommen. Was schiefe Ebene und Kräftezerlegung usw. angeht, war ich nie wirklich der Profi. Ich hätte hier zunächst für a) und c) die resultierende aus FG (bei c einfach FG) und F1 in FH und FN bei der schiefen Ebene zerlegt. Dann ist FN die Kraft in A und für jene in B zerlegt man FH in einen waagerechten (der wirkt auf B) und einen senkrechten Teil. Stimmt das soweit?

Für b) muss die resultierende von FG und F1 parallel zu FN stehen, damit FH nicht wirkt. Für F1> dieser Wert steigt die Walze. Korrekt?

Danke für eure Hilfe.

Hallo komme bei einer Aufgabe nicht weiter.

Auf einer schiefen Ebene mit einer Steigung von 10 % bewegt sich ein 700g schweres Fahrzeug mit einer permanenten Motorkraft von 1,5N entlang der Bahn nach oben (keine Reibung). Am Anfang hat er eine Geschwindigkeit von 1km/h.

a) Wie weit fährt der Wagen, bis er die Geschwindigkeit verdoppelt hat?

Wie komme ich da weiter? Habe den Winkel ausgerechnet und die Hangabtriebskraft

Wie kann ich mir diese Formel gedanklich vorstellen: F=m*a

Z.B:

w=2π/T

w=2π*f

w=v/r

Weil ein 40kg Zementsack sollte man tragen können wurde mir gesagt

Moin, wann setzt man F rück mit F Gravitation und wann mit F gesamt gleich. Ist es bei einem vertikalem Federpendel die Gravitation und bei einem ebenen die Gesamtkraft. Oder liegt es daran ob man eine Differntialrechung lösen möcjte und daher a braucht da dies die 2 ableitung von s ist (ich weiß dass 9,81 eigentlich a ist).

Ist es rein theoretisch möglich, dass dieses Phänomen vorkommt - der Fluss wie gewohnt weiter fließt und sich dessen Wasser mit dem eines Sees vermischt?

Außerdem: Was würde passieren, wenn man einen großen Fluss durch Menschenhand mit einem See verbindet? Könnte es sein, dass der Höhenunterschied vom See dafür sorgt, dass sowohl See als auch Fluss weiter gemeinsam existieren?

Bekomm den Deckel einfach nicht aufgedreht 😅 der ist relativ groß, also passt gerade so in meine Hand.

Ist aus Plastik, daher funktioniert es auch nicht mit irgendwelchen anderen Sachen oder mit dem Unterheben-luft-rein-trick und ich wohne alleine, also kann auch niemanden sinnvolles fragen

Hat wer eine Idee haha

Ich suche jetzt schon seit einer Stunde erfolglos nach dem englischen Wikipediaartikel zur Hangabtriebskraft. Vielleicht liegt es daran, dass ich nicht das richtige englische Wort dafür gefunden habe, allerdings gestaltete sich die Suche danach ebenfalls schwierig.

Gibt es überhaupt einen solchen Artikel und wenn ja, wie heißt dieser?

Kann mir jemand bitte helfen bei der Aufgabe.

Bin besonders durch die m s^-2 Vorzeichen und alles unsicher ob das richtig ist.

Hallo kann mir jemand dieses Beispiel erklären wie man auf 4 kommt? Ein Stein, den du vom Balkon E2 im ersten Stock fallen lässt , prallt mit einer bestimmten Geschwindigkeit am Boden auf. Aus dem wievielten Stock muss er fallen, damit die Geschwindigkeit am Boden doppelt so groß ist? Und wie wäre das am Mond (wenn es dort Häuser gäbe)?

Wie lassen sich Aufgaben

1. a) b)
2. b)

lösen?

Vielen Dank für alle Erklärungen, Hilfestellungen und Ansatzgleichungen

Schönen Abend allen :)

Oder beschrieben sie das selbe ?

es gibt ja die Formel F=m*g.

also da kann ich als Gewichtskraft 100N einsetzen, das ist nach m umgestellt dann F/g, also so in etwa 10kg.

heißt das, dass 100N dann 10kg entsprechen? Ist das dann das selbe? Wenn ich 70kg wiege, kann ich dann auch sagen, dass ich etwa 700Newton Gewichtskraft habe?

Hallo hier habe ich 2 Aufgaben :

Ich weis nicht wie man hier rechnen soll ? Mit Impulserhaltungssatz ? Oder anders ? Kann jemand helfen ?

Ich weiß nicht wie ich die Aufgabe lösen soll und muss es für diesen Montag lösen. Jimmy läuft auf einem zugefrorenen Teich Schlittschuh. Seine Geschwindigkeit beträgt 9,0 meter pro sekunde und seine Masse ist m1. Es wird angenommen dass keine Reibung herrscht.

1. Beschreiben Sie die Art von Jimmys Bewegung.
2. Ein Kamerad mit einer Masse von m2 = 0,9 • m1 bewegt sich mit gleicher Geschwindigkeit in entgegensetzte Richtung auf Jimmy zu. Nach dem Zusammenstoß steht Jimmy bewegungslos auf dem Teich. Berechnen Sie die Geschwindigkeit des Kameraden nach dem Zusammenprall, wenn man annimmt, dass er sich in gleicher Richtung zurück bewegt.

Ich denke dass man hier einen Elastischen Stoß hat und das ich die formel p(nacher)= p(vorher) benutzen kann.

Beschleunigte Bewegung mit Anfangsgeschwindigkeit.

Das Gravitationsgesetz lautet ja F = G·m₁·m₂:r². Aber wieso wird der Abstand r quadriert? Wieso nicht hoch 3 oder einfach nur r?

Also ich weiß, wie ich die Beschleunigung berechne, aber was ist mit „zur Zeit der größten Elongation“ gemeint?

Hey, ich brauch zwei Namen für zwei Gruppen. Die eine Gruppe will den Frieden für ihre Spezies komme was wolle und die anderen wollen es ohne jegliche gewalt lösen. Die Mitglieder der Gruppen haben verschiedene Fähigkeiten und charakter.

Wäre cool wenn jemand Ideen hätte. :)

Guten Abend,

kann jemand für mich überprüfen, ob ich die Aufgabe richtig berechnet habe? Ich habe nicht gerundet, habe jedoch zwei leicht von sich abweichende Ergebnisse erhalten.

Zudem habe ich noch keine Idee, woher der Zahlenwert für die Gravitationskonstante g = 9,81 N/kg kommen könnte.

Bitte so ausführlich wie möglich erklären, das würde mir wirklich sehr helfen.

Was glaubt ihr,

Welcher Hund den stärksten Biss hat?

Sollten eurer Meinung nach Rassen fehlen die in dieser Kategorie passen ergänzt sie in den Kommentaren

Aufgabe 3)

Wir haben zwei Körper. Genau Identisch. Aber sie haben eine unterschiedliche Masse. Beide haben den selben Luftwiderstand und das Experiment findet auf der Erde statt.

wer ist zuerst am Boden? Der schwere oder leichte Körper?

Hallo Leute, ich weiß nicht wie ich beim unten gezeigten Blatt die Kraft einreichen soll. Ich weiß dass mann dazu einen Pfeil einzeichnen muss und eine Klammer, aber ich weiß nicht wirklich wo und wie ich da anfangen soll. Weiß jemand weiter?

Ich benötige zu Aufgabe Nummer 2

Hey,

ich verstehe nicht wie ich bei der 4.Aufgabe an die Geschwindigkeit am Aphel kommen soll. Könntet ihr mir einen Ansatz geben und sagen wie man ab da weiter macht?

Ja. Also warum ist die Gravitationskraft in dem Fall die Zentripetalkraft

Hallo, ich habe in Physik neulich eine Aufgabe gerechnet und bin mir nun nicht sicher ob es richtig ist. Wär lieb, wenn ihr mal drüber schauen könntet :)

Aufgabenstellung:

Der Fahrer eines Pkw (v = 50 km) sieht einen Ball auf die Straße rollen und bremst. Auf trockener Straße hat das Fahrzeug bei Vollbremsung eine Bremsverzögerung von 6,6 m/s2. Die

Masse des Pkw beträgt 1 200 kg.

1. Wie groß ist die wirkende Bremskraft? Berechne.
2. Bestimme den Bremsweg.
3. Wie verändert sich der Weg bis zum Stillstand, wenn man die „Schrecksekunde" des Fahrers berücksichtigt?

Hier kommt meine Lösung dazu:

Ich habe gesehen als ich in Wohnzimmer spilzimmer da war habe ich ein gesehen das ein gegenstand ohne das ich es angefast habe sich Bewegt hat und so was habe ich oft erlebt in mutter kind haus wo ich wohne wenn ich sowas mitbekommen habe war ich aleine als ich es sa mache es mir angst gr Eli

Hallo kann mir jemand mit der nummer 4 helfen?

Dankee!!

Frage zu der untenstehenden Aufgabe, wie man diese löst und darunter kommen meine Gedanken zu der Aufgabe (mit denen ich aber nicht richtig weiterkomme).

Ich habe in Physik diese Aufgabe bekommen:

Hakt man eine Kugel an eine entspannte Schraubfeder, die an einem Stativ hängt, und lässt die Kugel los, so zieht sie diese Feder um das Doppelte der Strecke nach unten, die sich ergibt, wenn man die Kugel langsam mit der Hand nach unten führt, bis sie ihre Gleichgewichtslage, an der der Feder hängend, erreicht hat. Zeigen Sie, dass diese Beobachtung mit dem Energieerhaltungssatz übereinstimmt.

Mein Lösungsansatz dafür wäre, dass man erstmal zwei Versuche annimmt, die eine gemeinsame Ausgangslage 0. haben:

0 . Die Feder ist entspannt, und das Massestück ist erstmal noch fest.

1. Wenn die Kugel mit der Hand nach unten geführt wird, bis sie ihre Gleichgewichtslage, an der Feder hängend, erreicht hat.
2. Wenn die Kugel einfach so losgelassen wird und die Feder um das Doppelte der Strecke von 1. nach unten gezogen, bis sie auch ihre Gleichgewichtslage erreicht hat.

Mein Gesamtgedanke war, dass die potenzielle Energie von 0. bei 1. in Spannungsenergie und kinetische Energie der Hand umgewandelt wird, bei 2. nur in Spannungsenergie.

Bei 0. wirkt die Gewichtskraft auf das Massestück mit Fg= m*g.
Dabei hängt das Massestück über einer bestimmten Höhe h über dem Nullniveau des Bezugskörper Erde.
Die Federspannkraft bei 0. Fsp ist gleich 0 N, weil die Feder entspannt ist und der Weg der gespannten Feder s=0m ist.
Die Formel für die Federspannkraft ist Fsp= D*s.
Bei beiden Versuchen bleiben die Masse m, die Fallbeschleunigung g und die Federkonstante D gleich. Deswegen ist die Gewichtskraft bei beiden Versuchen gleich. Jedoch ändert sich der Weg s und die Höhe h bei beiden Versuchen und damit auch die Federspannkraft.

Die Spannkraft Fsp wirkt in die gleiche Richtung wie die Gewichtskraft Fg und den Weg s.

Bei 1. wird die Feder nun mit der Hand um die bestimmte Länge s gedehnt, die Höhe h ändert sich, indem h1=h - s. Mit der Hand führt man eine Bewegung aus, weswegen ich meinen würde, dass dort auch irgendwie kinetische Energie ins Spiel kommt?

Bei 2. wird die Feder um den Doppelten Weg s von 1. , also 2*s, gedehnt und die Höhe h ändert sich, indem h2=h - 2*s.

Bei 0. ist keine Spannkraft vorhanden, also auch keine Spannenergie. Es ist aber die Gewichtskraft vorhanden, weswegen es eine potenzielle Energie Epot gibt. Diese ist Epot = m * g * h.
Bei 1., wie auch 2., wird die potenzielle Energie Epot in jeweils unterschiedliche Spannenergie umgewandelt, weil bei 1. und 2. Spannkraft unterschiedliche Fsp vorhanden ist. Diese hängt ausschließlich vom Weg s ab.

Ich würde jetzt davon ausgehen, dass bei 1. der doppelte Weg 2*s durch die Hand und das Massestück vollführt würden (gleichzeitig und deswegen ist das die Hälfte von Weg 2*s in 2.), während bei 2. die Hand wegfällt und somit der Weg s von der Länge her, doppelt so lang ist, wie der in 1. .

Aber jetzt komme ich nicht weiter... Und ich weiß auch nicht, ob ich irgendetwas falsch gemacht habe, aber ich hoffe, ihr könnt mir helfen:D

Viele nennen es heutzutage „Gym“. Das ist erst seit weniger Jahren so und wird oft von der Jugend gesagt. Deshalb hier die Frage, was sagt ihr zu diesem Ort, an dem man trainiert? Schreib gegebenenfalls auch das Baujahr/Alter.

Hallo miteinander, zur Zeit befasse ich mich mit der Thematik der Statik in Fachwerken. Meine Frage bezieht sich auf die Thematik zur Ermittlung von Nullstäben in einem Fachwerk. Der Sachverhalt kann dem beigefügten Bild entnommen werden.

Meine Frage ist warum die markierten Stäbe nach der ersten Regel Nullstäbe sein sollen.

Bei Betrachtung des Knoten 3 wirken keine Kräfte. Jedoch Wäre mein Gedankengang so, dass die Reaktionskraft des Festlagers linear verschiebbar ist und somit auf der Wirkungslinie des vertikalen Stabs von 3 wirkt, und somit kein Nullstab sein kann und bloß der horizontale Stab als Nullstab gilt.

Liegt es daran, dass bei der Ermittlung von Nullstäben alle Knoten separat betrachtet werden und bei der Ermittlung die Kräfte nicht linear verschoben werden (dürfen)?

Hallo,

ich habe eine Frage. bzw 2 Fragen. Wenn man sich die Kraft aufteilt, um die resultierende Kraft zu "tragen", sind die Teilkräfte addiert immer größer als die resultierende Kraft. Wie kann das sein, bzw warum ist das so? Meine Lehrerin hat mir erklärt, dass es daran liegt, dass manche Ausführung, also wie man es hebt, schwerer sind. Natürlich hat es etwas mit dem Winkel zu tuhen. Aber wenn man sagt, dass eine bestimmte Anzahl an N ein Gewicht hebt, wie kann man dann sagen, dass eine Ausführung (hat meine Lehrerin gesagt) mehr Newton braucht? Außerdem würde mich grundsätzlich das Konzept vom Kräfteparallelogramm interessieren. Warum ist es logisch, dass wenn man Teilkräfte mit einem bestimmten Winkel einzeichnet, die resultierende Kraft erhält?

Ich freue mich über jede Antwort!

Die Aufgabe lautet wie folgt:

Ein Auto fährt zum Zeitpunkt 0s mit einer konstanten Geschwindigkeit von 54 km/h. Zum selben Zeitpunkt, aber in 150m Entfernung fährt ihm ein LKW entgegen. Dieser beschleunigt gleichmäßig mit 4 m/s^2. Bestimme wann und wo die beiden zusammentreffen.

Zum Kontext, wir haben vor kurzem angefangen mit den Formeln s(t) = 1/2at^2 und v(t) = at angefangen zu rechnen.

Eine Lösung mit Erklärung wäre nett. Schönen Tag noch

Wieso setzt er hier FZ = FG bei a) und wieso ist omega = v * r und Omega = 2pi/T, also wieso kann man die gleichzeitig anwenden?

Wieso reicht es wenn die Winkelgeschwindigkeit gleich groß ist und wieso ist r automatisch der Abstand des erdmittelpunktes vom Satelliten?

Quelle: https://www.youtube.com/watch?v=NKwjgMus2Jg&t=426s

Hey Leute, morgen schreibe ich einen Physik Test.. Leider verwirrt mich das immer noch mit den ganzen Einheiten (mikro, milli, kilo und so) muss man da immer wenn zb in der Aufgabe steht 1 Kilo in mikro umwandeln 6 Nullen hinzufügen oder wie viele😬 ich kann das alles garnicht..

Wir hatten es heute mal wieder von Arbeit.... Das geht absolut nicht in meinen Kopf.
Warum sollte man das ausrechnen wollen und wofür wird das verwendet? verstehe es von vorne bis hinten nicht.

Hallo,

die Federkonstante beschreibt, dass die Verlängerung mit der Kraft in einer proportionalen Beziehung steht. Dies kann man durch einen Graph festellen und die Steigung wäre dann : Kraft/ Verlängerung= D. ich verstehe jedoch nicht ganz logisch die Formel, bezogen auf die Federkonstante. Ich versteh den mathematischen Sinn und kann auch damit rechnen, jedoch würde mich interessieren, warum die Formel genau so aufgestellt ist.

Hallo, ich habe folgende Aufgabe in Physik:

Ein Kraftfahrzeug wird aus 120 kmh' bis zum Stand abgebremst; der Bremsweg beträgt 115 m. Wie groß ist a) die Bremszeit, b) die Bremsverzögerung?

Welche Formel muss ich hier nehmen, ich habe an s=1/2a*t^2 gedacht aber das kann ich ja nicht nehmen weil meine Anfangsgeschwindigkeit nicht 0 ist sondern 120 km/h.

Danke für eure Hilfe!

Wir haben eine Physik Lk geschrieben und folgende Aufgabe hatte ich falsch. Könnte die mir jemand erklären.

Wenn die Freundin stärker ist meine ich. Was denkt ihr? Wäre es euch peinlich?

Hallo,

Sicherlich kennt ihr dass...

Ihr braucht einen Wert bei dem ihr echt sicher sein könnt, dass ein Bruch stattfindet. Gibt eine Richtlinie als eine Art Angabe in Kg oder Nm oder irgendwie so etwas um zu bestimmen ab wann ca. ein Kniegelenk von der Seite zertrümmert werden kann oder ab wann ein Elenbogengelenk gegen den Winkel belastet bricht?

Also Bsp. Ein Mensch der ca 30 Kniebeugen schafft kann bei seitlichem tritt gegen das Kniegelenk zu 100 % das Knie eines für ewig verkrüppeln.

Oder ein Mensch von ca. X Kg der 10 Klimmzüge schafft, kann auf seiner Schulter den Arm/das Elenbogengelenk einer anderen Person, entgegen der Dehnrichtung brechen soweit er Vollgas gibt....

Gibt es irgendwo Zahlen nach denen sich Eie Person richten kann was das angeht?

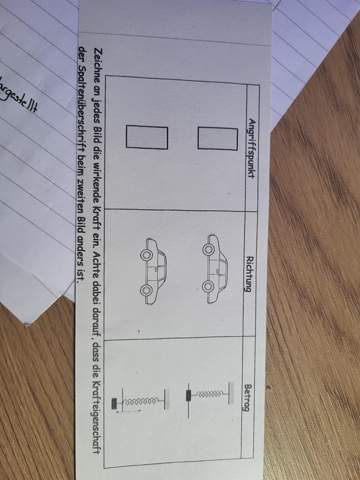
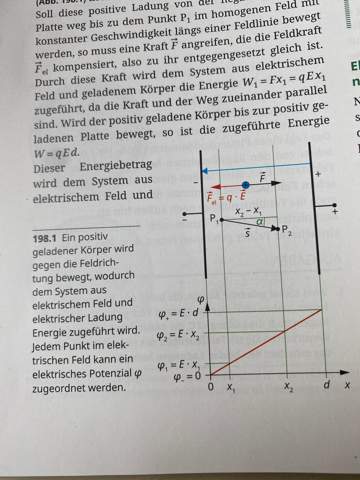
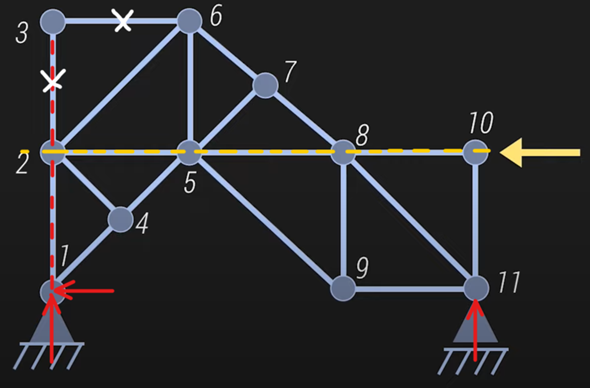
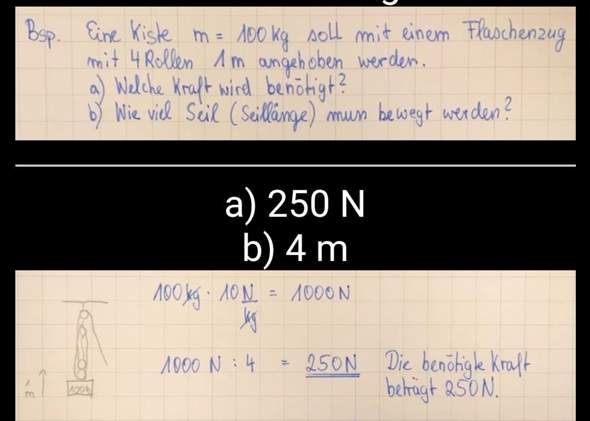
Fatto diretto al punto (Ich komme direkt zum Punkt, wie der Italiener sagen würde).

Ein zylinderförmiger Elektronenstrahl hat einen Durchmesser von 0.5 mm. Der Strahl enthält 2 × 10^8 Elektronen pro Kubikmillimeter. Die Energie der Elektronen beträgt 0.3 keV.

a) Wie schnell sind die Elektronen im Elektronenstrahl?

b) Berechnen Sie den elektrischen Strom.

c) Der Elektronenstrahl durchläuft ein transversales magnetisches Feld von 2 Tesla. Berechnen Sie den Krümmungsradius der Kreisbahn im Magnetfeld.

Jensek81'scher Ansatz

a) E_kin = 1/2 m v²

Umformen zu v = Wurzel (2 E / m)

E = 0,3keV = 0,3 * 10³ * (1,6022*10^-19)

m = 9,11*10^-31 kg

Einsetzen: v = Wurzel (2 E / m) = v = Wurzel (2 * 0,3 * 10^-3 / (9,11*10^-31 kg))

= 10272468,08 m/s

b) Stromstärke Elektronenstrahl

I = n * e * A * v

n = Dichte = 2 * 10^-8 e/cm³ = 2*10^-14 e/m³

e = 1,6022 * 10^-19 C

A = π r², wobei d = 2 * r (da Zylinder) =>> 0,5 mm = 2 * r => r = 0,25 mm = 0,00025 m

V = 10272468,08 m/s (aus vorheriger Aufgabe)

Einsetzen: I = n * e * A * v = 2 * 10^-14 e/m³ * 1,6022 * 10^-19 C * π * (0,0025m)² * 10272468,08 m/s

= 6,46 * 10^-5 A

c) r = (mv)/(e*B)

= (9,11*10-31 kg * 10272468,08 m/s) / (1,6022*^10^-29 * 2 T) = 2,92*10^-5 m

Stimmt das so? Insbesodnere die 10272468,08 m/s erscheinen mir doch sehr skrupellos...

Hallo,

Das Wechselwirkungsprinzip geht davon aus, dass auf jede Kraft, eine gleich große entgegengesetze Gegenkraft wirkt. Dies kann man auf viele Beispiele aus dem Alltag beziehen. Beispielsweise das Aurofahren. Jedoch blieb mir ein Gedankenexperiment unbeantwortet:

Stellen wir uns vor ein Mensch bringt so eine Muskelkraft auf, sodass er ein Auto schieben kann. Der Mensch hat eine kleinere Masse als das Auto und somi5 ist das Auto träger. Was ich jetzt nicht verstehe: wenn auf die Person die gleiche Gegenkraft wirkt, die er ausgesetzt hat auf das Auro, warum spürt er dann keine Folgen, wie zum Beispiel, dass er weggeschubst wird oder sowas. Ich weiß, dass es in der Realität nicht so ist, jedoch verstehe ich nicht so ganz warum.

Ich hoffe jemand kann mir helfen.

Ich danke für jede Antwort

İch habe sehr sehr lange gebraucht und etwas heraus bekommen jedoch bin ich nicht wirklich zufrieden und stark unsicher, vlt könnte jemand diese mir nehmen, ist nicht mehr weit bis zur Abgabe.

Ergebnis (vermutlich inkorrekt):

Die Gravitationsbeschleunigung auf dem Mars beträgt etwa 1,5 m/s^2. Die Rotoren auf dem Mars müssen sich mindestens 9 Umdrehungen pro Minute drehen.

kann mir jemand eine formel geben?

Folgende Situation:

Das Objekt ist ein Taschenrechner, der langsam vom Tisch fällt, wie wenn man ihn runter geschoben hat. Der Tisch hat eine Höhe von 75 cm und kann auch nicht durch das Gewicht vom Taschenrechner zerbrechen. Man selber steht vor dem Tisch und spürt ein kleines Erdbeben durch den Aufprall des Taschenrechners.

Wie schwer ist der Taschenrechner?

An einer Rolle an der Decke hängen auf der einen Seite ein Sack mit 80kg und auf der anderen Seite des Seil eine Person mit exakt dem selben Gewicht. Beide hängen in der Luft und haben keinen Bodenkontakt. Was passiert mit dem Sack, wenn die Person anfängt das Seil hochzuklettern ?

Reibung kann unberücksichtigt bleiben.

danke!

Hallo, kann mir jemand bitte den Lösungsweg erläutern? Ich komme bei der Aufgabe nicht auf die richtigen ergebnisse.

Bei F1=5,862kN

Bei F2=3,901

Hallo,

es geht um Bezugssysteme in Physik:

Wenn ich still in einem fahrenden Zug sitze, wäre dann ein Bezugspunkt der Zug, gegenüber dem ich mich nicht bewege, und ein anderer Bezugspunkt der Bahnhof, gegenüber über dem ich mich mit dem Zug sehr schnell bewege?

Ich habe mal die Nummer 1 im Buch und meine Aufgaben dementsprechend hochgeladen… bin auf eure Meinung gespannt ob ich es richtig gemacht habe…

die frage ist in einem 1gegen1 und nicht durch einen hinterhalt

Eine Pendelkugel trägt die Ladung Q = 52 C und hat die Masse m = 0,4 g. Sie hängt an einem Faden der Länge I = 1.8 m in einem horizontal gerichteten homogenen elektrischen Feld. Durch die Kraft des Feldes wird sie um d = 15 mm ausgelenkt. Berechne die Feldstärke des homogenen Feldes.

wie skizziere ich das?

Hallo,

Ich habe mich heute etwas mit dem Trägheitsgesetz auseinandergesetzt und habe paar Fragen. Das Trägheitsgesetz geht davon aus, dass ein Körper in seiner Bewegung unveränderlich bleiben will und wird, solange keine andere Kraft auf dieses Objekt/den Körper wirkt. Damit der Körper in seiner Bewegung unveränderlich bleibt, setzt er eine entgegengesetzte Kradr aus, um seinen Bewegungszustand zu behalten. Dazu habe ich mir folgendes Expermiment angeschaut: ein Stein wird auf einer Karte platziert und die Karte auf einem Becher. Der Stein steht im ersten Moment still und will auch still bleiben, dass bedeutet gleichzeitig auch, dass er auf der Karte bleiben will (wenn er runterfällt, würde ja sein Bewegungszustand verändert werden). Wenn man ja sagt, dass ein Körper träger ist, bedeutet dies ja, dass es besser seinen Beweugungszustand beibehalten kann. Wenn wir jedoch die Karte schnell wegziehen, kann der Stein nicht (habe ich so gelesen) reagieren und fällt runter. Je größer die Masse, desto träger ein Körper. Aber warum fällt dann ein schwerer Stein dann schon bei langsamen wegziehen runter und ein kleinerer (kleinere Masse) nicht? Wenn es ja träger ist. Ich glaube ich habe einen kleinen Denkfehler, aber komme gerade nicht auf die Lösung. Außerdem weiß ich noch, dass man zwischen stillstehenden Körperen und sich bewegenden Körpern unterscheiden muss. (Bewegende Körper wollen ihrer Bewegungszustand beibehalten, also bei einer Bremsung gehen wir auch im Auto nach vorne). (Wenn wir aber still stehen, wollen wir ja still stehen bleiben).

Kann mir jemand dieses Experiment ganz genau erklären, wie welche Kräfte wirken?

Zudem, ich versteh zwar gut warum wir beim bremsen nach vorne gehen. Jedoch verstehe ich nicht ganz, warum man beim Beschleunigen in den Sitz gepresst wird. (Ist es weil wenn wir beschleunigen, gehen wir ja nach vorne, unser Körper jedoch, will seinen Bewegungszustand nicht wechseln und wirkt mit einer Kraft entgegen?)

Hallo, gibt es eine (Luft)pumpe/kompressor bei welcher man den lufteingang sieht? Ich bräuchte soeine nähmlich. Gibts das auch für unter 30€? Muss nicht zu viel druck haben

MFG

Hallo,

heute in Physik haben wir gelernt, dass ein Federpendel bei jedem Ortsfaktor gleich schwingt. Deshalb benutzen Astronauten auch ein Federpendel, um sich zu wiegen.

Nun ist meine Frage, wieso das denn so ist, denn FG ist ja eine zusätzliche Kraft, die am Objekt an der Feder "zieht". Demnach müsste die Amplitude "nach oben" ja kleiner sein als "nach unten", eben weil eine Kraft das Objekt nach unten zieht. Wieso hat die Kraft denn anscheinend keine Auswirkungen auf das Objekt?

Danke

Durch Anwendung einer konstanten Bremskraft F wird die Geschwindigkeit eines Autos der Masse m= 800kg innerhalb von 5s von 90km/h auf 60km/h verringert. Bestimme die Verzögerung und die konstante Bremskraft.

Die Aufgabenstellung steht oben. Die Masse bleibt gleich. (Fahrradfahrer 55kg wird 1.aus Stand auf 5m/s dann aus 5m/s auf 10m/s beschleunigt.)

Denn ich denke, dass E kin gleich sein sollte, da

E kin = ½ • m • v²

Und da ◇v1 = v1 - v(Stand) = 5m/s - 0m/s

Und ◇v2 = v2 - v1 = 10m/s - 5m/s

(◇ = Änderung)

Ja das gleiche ergeben (5m/s).

Deshalb sollte die gleiche Energie benötigt werden oder?

Da wir 2 Teilaufgaben dafür haben und es keinen Sinn machen würde, wenn wir 2 mal das gleiche ausrechnen.

LG, Mayu :)

Quasi von Ende 12 bis 47.

Der Mensch kann sich an der Pubertät 35 Jahre lang gut mit allen Altersgruppen körperlich durchsetzen und dann war’s das auch oder?

Sind Fleissige Menschen fleissig geboren? Weil ich war nie fleissig, und immer wenn ich versuchte sehr fleissig zu sein, sah ich denn Sinn darin nicht.

Ich hatte nie grosse Ziele, nie grosse Wünschen, auch nicht als Kind. Als Kind haben ja viele einen grossen Wunsch, später mal Astronaut werden, oder Pilot oder so. Natürlich ist das meist nicht realistisch, aber ich hatte als Kind nie einen grossen Wunsch.

Später hatte ich nie einen Karrierewunsch, oder Jobwunsch. Ich hatte nie grosse Träume, nie grosse Ziele, ich existierte schon immer nur vor mich hin, und liess mich treiben.

Und vielleicht war ich zu faul, ich hab dann angengagen immer auf kosten andere zu Leben, einerseits weil ich echt keine Motivation oder kraft hatte, andererseits Faulheit.

Ich habe keine Traumkarriere, keine besondere Interessen, nichts wofür ich brenne, hatte ich nie.

Woran könnte das liegen, und wie bedenklich ist das? Ich meine ich will etwas produktiver werden damit ich selbständig leben kann, aber jetzt grosse Karriere machen? Wahrscheinlich eher nicht.

Ist das schlimm? Ist auch schwierig motiviert zu sein wenn man immer schlapp ist.

Hallo, wieviele 16 Jährige Mädchen würden es brauchen einen 16 jährigen Jungen zu überwältigen und zu fesseln. (er ist 170 und wiegt ca.64kg)

Eine Frage in Physik?? Ich brauche eure Hilfe!!!!

Danke

Auf der Luftkissenfahrbahn fahren Wagen mit der Masse 100g und 150g mit der Geschwindigkeit 0,8 m/s aufeinander zu. Nach dem Zusammenstoß hängen die Wagen aneinander.

a) Berechne den Impuls der Wagen vor dem Zusammenstoß

b) Berechne die Endgeschwindigkeit der Wagen.

Problem/Ansatz:

Ich bin mir generell nicht sicher, ob es richtig ist:

a)

p = m * v

100g = 0,1 kg

150g = 0,15 kg

P₁=m₁*v₁= 0,1kg * 0,8 m/s = 0,08 kg*m/s (bewegt sich nach links, also negativ)

P₂=m₂*v₂= 0,15kg * 0,8 m/s = 0,12 kg*m/s (bewegt sich nach rechts, also positiv)

Damit wäre a beantwortet und wir beschäftigen uns mit der b

b) Hier habe ich keinen Ansatz

Wie viele Liegestütze muss ich täglich machen um ein Auto hochheben zu können? Wie lange dauert das? Und wie viele Liegestütze wären das insgesamt? Bitte nur ernstgemeinte Antworten.

Die Gleichung n^2 * h^2/(8ma^2) beschreibt die zulässigen Energiezustände eines Teilchens in einem eindimensionalen Kasten, wobei n = 1, 2, 3, ... Die Gleichung hängt nicht von der Geschwindigkeit des Teilchens ab, aber warum?

Angenommen, ich werfe das Atom jedes Mal mit einer zufälligen Geschwindigkeit, die zu verschiedenen Translationsenergien führt, decken dann alle möglichen "n's" in der Formel alle möglichen Geschwindigkeiten ab?

Mir ist klar das eine Zustandsfunktion unabhängig vom Weg ist. Zum Beispiel ist die Potentielle Energie wenn ich etwas anheben von h=0m zu h=8m immer die gleiche, egal ob ich dabei von links nach rechts oder im Kreis Schwenke, am Ende kommt es nur auf anfangs und Endzustand an.

Arbeit ist W = F*d, doch warum ist das nicht auch eine Zustandsfunktion? Angenommen ich stehe am fuß eines Berges, ein Freund geht direkt straight von unten zur Spitze (Weg 1) und ich gehe in einer Spirale nach oben (Weg 2), dann haben wir doch trotzdem am Ende die gleiche Arbeit gegen die Gravitationskraft geleistet obwohl wir unterschiedliche Wege genommen haben, selbst wenn ich hoch und runter gehe aber am Ende oben an der Spitze lande, dann habe ich beim runtergehen ja negative Arbeit und beim hochgehen positive geleistet und in der Summe kommt das gleiche raus.

Um 100 Kg 1 m zu heben braucht man iwie 1000 N oder so

Aber es ist doch so

Wenn ich 100 Kg in 1 Sekunde um 1 Meter hebe, brauche ich doch weniger Kraft,

als wenn ich mir 10 Sekunden Zeit lasse 100 Kg um 1 Meter zu heben.

Warum wird die Zeit bei der Kraft nicht berücksichtigt? Waren die Physiker noch nie im Fitness-Studio?

Introversion ist ein Phänomen, das nicht nur theoretisch existiert, sondern auch im Gehirn messbar ist. Das Merkmal ist, dass introvertierte Menschen regelmäßig Zeit für sich allein brauchen, um ihre Energie wieder aufzuladen, denn Gesellschaft ist für sie anstrengend.

Bei mir ist diese Introversion so stark ausgeprägt, dass ich irgendwann körperliche Erschöpfungszustände erlebe, nur weil ich zu lange zu wenig für mich und in der Ruhe war.

Irgendwann spüre ich Dinge wie

- Sekundenschlaf

- extreme Müdigkeit

- emotionale Instabilität, Hang zur Weinerlichkeit

- Konzentrationsstörungen

- Schwindel, Kreislaufprobleme

Usw. Halt alles mögliche an Erschöpfungssymptomen.

Ist bei euch anderen Introvertierten diese Eigenschaft auch so stark ausgeprägt und steht sie euch im Leben auch manchmal spürbar im Weg oder bringt euch an eure Grenzen?

Angenommen man würde ein Seil an zwei unterschiedlichen hohen Decken befestigen:

Normalerweise (also bei einer normalen Decken, also bei nur einer Decke, also so wie bei einer Spielplatz Schaukel, wo beide Seiten des Seiles gleich weit von der Decke entfernt sind) würde sich das Gewicht ja auf beide Seiten gleichmäßig verteilen.

Wie verhält sich das bei 2 unterschiedlich Deckenhöhen?

Trägt die rechte Seite mehr Gewicht, weil da mehr Seil ist? Oder trägt die linke Seite mehr Gewicht, weil diese näher am Körper ist?

Und angenommen die linke Decke würde aus, mir fällt jetzt nichts ein, aber sagen wir mal aus einem ganz leichten Material bestehen, sagen wir mal aus Schokolade bestehen

Und die rechte Decke würde aus Beton bestehen.

Dann würde sich das Gewicht trotzdem auch auf beide Decken gleichmäßig verteilen? Auch wenn die Schokoladendecke dann zusammenbrechen würde?

Es sei denn man hält sich mit seinem rechten Arm stärker an der rechten Seite des Seils fest?

Hilfe

Ich brauche eure Unterstützung bei dieser Physikaufgabe

Eine PKW mit Vorderradantrieb hat eine Masse von 1,546 t und einen Radabstand von 2,71 m. Sein Schwerpunkt liegt ca. 0,6 m über dem Boden und 1,2 m vor der Hinterachse.

Berechne für eine Haftreibungszahl von 0,6 die maximal mögliche Beschleunigen?

Hier ist eine Aufgabe, vielleicht könnt ihr sie beantworten

Die Frage klingt vielleicht ein bisschen dumm. Ich würde gerne erklärt haben wollen von jemandem, der sich auskennt, was eigentlich Gravitation bewirkt, wo kommt sie her, warum gibt es sie überhaupt?

Hey,

lasst mal euren Gedanken freien Lauf; was wäre gerade eine unglaubliche physikalische Erfindung, die quasi ein Durchbruch wäre,

Beispiel (was auch echt geht): Tag-Nacht-Solarzelle

Hallo, bald ist bei mir in der Stadt bei der Berufsfeuerwehr Tag der offenen Tür und dort bietet sich an die Drehleiter zu besteigen. Ich bin zwar schonmal in 30m Höhe im Korb gewesen aber würde auch gerne die Leiter besteigen. Mein Problem ist jedoch das ich mir unsicher bin, da ich ein paar mehr Kilos auf den Rippen hab, falls ich abrutsche. Ich hab halt mit einem Kollegen schon minimal Stress gehabt weil er meinte ich schaffe nur 2 Sproßen und er sich cooler fand. Ich würde gerne am Tag der offenen Tür das gegenteil Beweisen. Hat jemand Tipps fürs besteigen und der Tipps gegen die Unsicherheit vom Sicherheitsgurt 😅

Vielen Dank im vorraus

Die Drohen hat zwei gegenläufige Rotoren mit einem Durchmesser von 1,2m und wiegt 1,8kg.

Die Erdathmosphäre hat in Bodennähe eine Dichte von 1,2 kg m−3 und eine Erdanziehungskraft von ca 9,81 m s-2. Hier hob die Drohne bei 500 Rotorumdrehungen pro Minute ab. Die Marsathmosphäre hat eine Dichte von 0,020 kg m−3. Der Mars besitzt einen Durchmesser von etwa 6,8 · 103 km und eine Masse von ungefähr 6,4 · 1023 kg und hat daher eine Marsanziehungskraft von etwa 3,695 m s-2

Wie schnell müssen sich die Rotoren drehen, damit die Drohne aufm mars abhebt? Ich hab bis jetzt nur die Idee gehabt über die Auftriebskraft zu gehen, aber irgendwie bekomme ich keinen Bezug zu den rotorenumdrehungen. Vielleicht hat ja einer von euch ne Idee. Danke schonmal für eure Antworten

Angenommen in Fahrtrichtung "schwebt" beim vorderen Auto ein Gegenstand "frei". Wirken bei auf diesen Gegenstand bei einem Auffahrunfall tendenziell weniger "Kräfte" als wenn das vordere Auto frontal in etwas prallen würde? Ich hoffe ich habe mich einigermassen verständlich ausgedrückt.

Am Tag Playboy und Nachts ein Rächer!

dachte geteilt durch 2 pi und dann beide seiten quadrieren dann *m1*g und dann :(m2+delta m) ??? oder erst ausklammern und dann -m2*s und am ende : durch s damit delta m alleine steht übrigens die 0,66 gehören dazu

In Nullkommanichts zerbeißen die eine riesen Wassermelone .

Müssen die Löwen sich in Acht nehmen ?