Integralrechnung – die neusten Beiträge

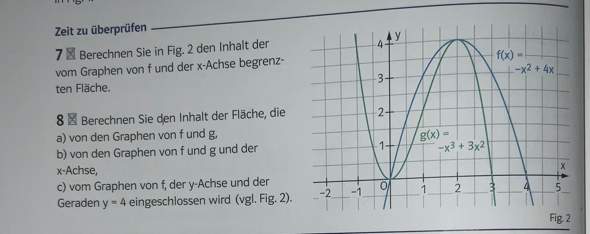
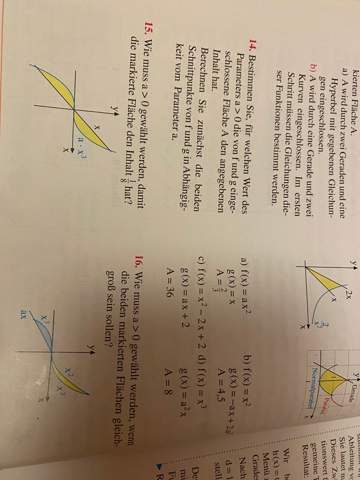
Mein Ansatz war es die Nullstelle Und Schnittstelle zu finden. Nullstellen sollten x=0 bzw Wurzel(8) sein. Die Schnittstelle habe ich mittels geogebra an x=4 herausgefunden, weil ich es rechnerisch nicht hingekriegt habe.

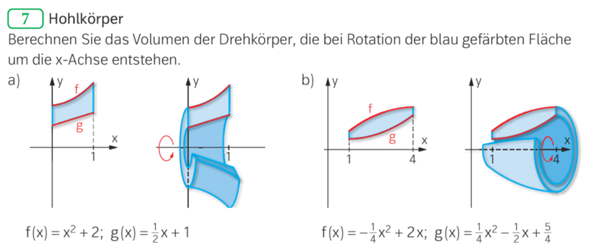
Nun meine Frage wie rechne ich den Rotationskörper, kann ich einfach V= pi*intergral von 0 bis 4 mit (f(x) - g(x)) ^2 rechnen?

Oder muss ich es getrennt wie folgt rechnen :

V1= Pi*intergal von 0 bis wurzel(8) mit (f(x)) ^2

V2= pi*intergal von wurzel(8) bis 4 mit (f(x) - g(x)) ^2

Danke für eure Hilfe!

Guten Abend!

Normalerweise habe ich ja keine mathematischen Fragen, vielleicht liegt es auch daran, dass ich ein wenig krank bin. :D

Also:

Ein Landwirt plant Neuerungen in der Bewässerung seiner Felder und eine Vergrößerung von Weideflächen. Er misst über 60 Tage hinweg die Durchflussmenge eines Bewässerungskanals.

Jetzt soll man berechnen, wie viel es in den 60 Tagen INSGESAMT war. Ich hätte dafür das Integral(D(t)) genommen. Stimmt das? Danke!

Gruß

Heyy,

Ich wollte fragen, wie man A1 und A2 berechnet.

Zu A1: stimmt das Ergebnis 0,301?

Gegeben sind die Funktionen f und g. Drücken sie den inhalt der beschriebenen Fläche mit A1, A2, A3.... aus und berechnen sie mit einem Integral.

f(x)=-x²+2

g(x)= 2x²-1

Hallo,

habe ich diese Funktion richtig integriert? Ich bin mir so unsicher dabei, die Stammfunktion zu bilden..

Da ich nicht wirklich weiss, wie ich die Extrem- und Wendepunkte einzeichnen soll.

Und ja, es ist nicht sehr ordentlich gezeichnet

Danke für die Hilfe im Voraus.

Moin,

ich wollte nur zu Überprüfung einmal fragen, ob das so stimmt wie ich mir das gedacht habe:

in diesem Zusammenhang beschreibt die Stammfunktion ja die zurückgelegten Kilometer. Heißt wenn man jz fragen würde: Wie viele Kilometer hat der Radfahrer nach 4 Stunden zurückgelegt würde man einfach das Integral von 0 bis 4 bilden oder?

und wenn man jetzt fragen würde: Wie viele Kilometer hat der Radfahrer in Stunde 4 zurückgelegt würde man einfach F(4) bilden oder?

Moin,

meine Frage ist, was die Stammfunktion im Sachzusammenhang beschreibt. Ich mein wenn ich jz eine Ausgangsfunktion f habe, welche die Zuflussgeschwindigkeit beschreibt weiß ich ja wenn diese unterhalb der x–Achse ist geht das Wasser z.B in einem Becken zurück. Aber was genau sagt mir die Stammfunktion dann?

f(x) = x^2 + 4x

und

f’ (x) = 2x + 4

Hallo, es wäre sehr lieb, wenn jemand mir verraten würde, wie man den folgenden Bereich zu skizzieren hat, und welche Grenzen man für y und x hat. Ich wäre sehr dankbar dafür.

Jetzt für jede Antwort DANKE!

Hey,

weiß jemand wofür die x achse steht?

Guten Abend,

Ich benötige einmal kurz eure Hilfe bei einer wichtigen Aufgabe, die so in der Art auch morgen in der Klausur vorkommen kann.

Hier die Aufgabe, es geht nur um Aufgabe a. Aufgabe b fand ich sehr einfach und konnte es entsprechend selbst lösen:

Gegeben sind die Funktionen f, g und h = f + g. Beurteilen Sie, ob die Aussage wahr oder falsch ist.

a) Wenn h(3) = 0 ist, dann ist f(3) = 0 und g (3) = 0.

b) Wenn f(7) > g (7) ist, dann ist h (7) > 0.

Danke im Voraus!

.

Hallo, kann mir einer sagen, was ich falsch eingetippt habe beziehungsweise was ich angeben muss, damit der Taschenrechner das Integral bestimmen kann?
Danke im Voraus für jede Antwort :))

1) Beurteilen Sie mithilfe von Material 1 die folgende Aussage:

Für 2 ≤ t ≤ 6 ändert sich beim Graphen jeder Stammfunktion G von g genau einmal das Krümmungsverhalten.

 g(t) t * e^(1-0,25t) 

Material 1 ist lediglich der Graph von

f a(t) = a *t*e^(-0,25t)

2)Ermitteln Sie mithilfe eines geeigneten Formansatzes eine Stammfunktion G von g.

[zur Kontrolle: G(t) = -4*(t+4) *  e¹-0,25*t ist die Funktionsgleichung einer möglichen Stammfunktion von g.]

3) Zeigen Sie, dass der Inhalt der Fläche, die der Graph von g im Intervall t ≥ 0 mit der t-Achse einschließt, endlich ist. Ermitteln Sie den Inhalt dieser Fläche.

Problem/Ansatz:

Kann jemand mir bei diesen Aufgaben helfen, wenn ich ehrlich bin ich sitze stumm vor dem Aufgaben und habe keine Ahnung wie genau ich die machen soll....

Bitte kann mir jemand da ganz schnell helfen??

Hallooooo

unten seht ihr zwei Aufgaben aus dem Lambacher Schweizer Qualifikationsphase (S.51 Nr.1+2), die ich von meinem Lehrer aufbekommen habe. Jedoch bin ich mir total unsicher, wie man dies nun berechnet. Es wäre mega lieb, wenn ihr mir weiterhelfen könntet, weil ich schon ziemlich lange verdutzt an meinem Schreibtisch sitze und immernoch keine Ahnung habe.
Ich danke euch schonmal im Vorraus!

Hallo,

wir schreiben in den nächsten Tagen einen Test zu Stammfunktionen, aber sehe da nur eher nicht durch.

Könnte mir jemand erklären, wie genau ich so eine Aufgabe lösen kann?

Mfg

Hallo liebe Leute,

ich habe eine Aufgabe wo ich geeignete Zufallsgeräte ausdenken muss. Leider stehe ich hier komplett aufm schlauch. Meine Idee war folgende:

a) 10 Flächiger Würfel: 2 Flächen: 6, 2 Flächen: 5, 2 Flächen: 4, 2 Flächen: 3, 2 Flächen: 3, 1 Fläche: 2, 1 Fläche: 1

jetzt hänge ich aber bei b und c. Was könnte hier für passende Geräte basteln ? Muss es zwingend ein Würfel sein ?

Ich bitte um Hilfe🙏🏼 Wie ist das Integral und wieso ist es besonders?

Ich würde gerne beide Funktionen gleichzeitig nutzen. Dies funktioniert momentan jedoch nicht, da beide die Variable x verwenden.

Kann man für eine der beiden Funktionen einstellen, dass bspw. y verwendet werden soll? In einem PDF zum Casio steht, dass bei Solve nicht unbedingt x die gesuchte Variable sein muss, jedoch wird nicht erklärt, wie sich das umstellen lässt.

Ich freue mich über jede Antwort!

Wie berechne ich diese Aufgabe?

Hallo!

Ich habe hier ein Problem mit dieser Aufgabe. Warum muss bei b) ∫f(x) 4;2 - ∫ g(x)3;2 gerechnet werden??? Kann man nicht gleich einfach nur ∫4;3 berechnen, nachdem man f(x)-g(x) gerechnet hat?

Und was muss man bei c) tun? Da ist nicht einmal eine Gerade gezeichnet, oder ist eine Konstante auf der Höhe y=4 gemeint?

Und woher weiß ich, wenn ich eine Fläche zwischen zwei Graphen berechnen möchte, ob ich f(x)-g(x) oder g(x)-f(x) rechnen muss?

LG

Hallo Leute, könnte mir jemand bei der Aufgabe 1 helfen?

a) ist positiv oder?

b)ist null aber warum

Und c?

Heyyy

ich lerne momentan für eine Mathe-LK Klausur und ich wollte fragen, wie man bei der Teilaufgabe c) vorgehen muss. Außerdem wollte ich gerne wissen, was denn das Integral der Funktion im Sachzusammenhang bedeutet.

Danke Im Voraus!

Kann mir jemand bitte sagen, was die Stammfunktion von f(x)= -x ist und erklären wie man darauf kommt. Ich tue mich schwer dabei. Dankeee

Welche Bedeutung hat es, wenn ich beim Integral die kleinere Zahl als Obergrenze benutze und die größere Zahl als Untergrenze? Bin nämlich auf eine Formel gestoßen, wo +unendlich meine Untergrenze ist...

Hallo,

mein Thema ist Nullstellen Berechnung. Ich habe die Nullstelle mithilfe der z substitution berechnet jedoch ist mein Ergebnis laut den lösungen falsch . Ich sehe keine Fehler könnt ihr mal nachschauen? Wäre mega nett

(sorry das Bild ist falsch rum)

Hallo, ich habe eine Frage bei einer Matheaufgabe.

Undzwar muss ich von der Kurve f(x)= 1/x die Ober- und Untersumme O6 und U6 bestimmen im Intervall 1-4, jedoch habe ich keine Ahnung, wie ich da vorgehen soll.

Bei O3 und U3 ging das ganze leichter, da konnte ich jeweils dies mit 3 Teilintervallenn berechnen, aber hierbei bin ich überfragt.

Wenn ich nämlich die Teilintervalle berechnen möchte, würde für eines 2/3 rauskommen, was absolut keinen Sinn ergibt???

LG

Ich versteh nicht ganz den Unterschied.

Soweit ich das aber noch verstanden habe, kann der Flächeninhalt nur positiv sein, weil Flächen ja nicht negativ sein können.

Und die Flächenbilanz kann auch negativ sein, wenn z.B. ein Teil des Graphen über der x-Achse ist und ein größerer Teil unter der x-Achse --> ,,mehr negative als positive Fläche"

oder? oder hab ich was falsch verstanden?

und wie berechnet man beide nochmal? Generell mit Integralen rechnen hab ich drauf, also muss das nicht nochmal erklärt werden sondern brauch eher eine allgemeine Formel wie man das berechnet.

danke schon mal!

Bestimme den Inhalt der Fläche, die vom Schaubild von f, der y-Achse und den Geraden g : y = -x -1 sowie h : x = 1/2 ln(2) eingeschlossen wird.

f(x) = -e^-2x -x -1

Aufgabe:

gegebene Funktion zur Aufgabe: "f"

f(x)= -e^(-2x) -x-1

Bestimme den Inhalt der Fläche, die vom Schaubild "f", der y-Achse und den Geraden

g: y= -x-1

h: x= 1/2 ln(2)

Habe mir mal die Funktion sowie die Gerade y über Geogebra eingezeichnet nur leider klappt es nicht mit der 2. Gerade x= 1/2 ln(2).

Hi, leider bin ich scheinbar für Aufgabe d) einfach zu blöd. Ich rechne seit einer Stunde daran herum und habe zwar die gesamtfläche mit 4*sqrt(3), aber es gelingt mir einfach nicht, eine Gleichung für die Parallele zu berechnen. Mein Rechner weiß leider auch nicht, was ich von ihm will (wer kann es ihm verübeln) und spuckt als einzige Lösung von Gleichungen "false" aus.

Kann mir BITTE irgendjemand weiterhelfen? Ich bin am verzweifeln.

Mit freundlichen Grüßen, Torty

Hallo! Ich habe eine Rechnung in Wolfram Alpha eingegeben, die Wolfram Alpha nicht ausrechnen konnte. Liege ich richtig damit, dass das hier Pi ergibt:

Der Strich am Ende ist nur mein Cursor.

Das glaube ich, weil ich mir das so hergeleitet habe:

Wenn ich mir mal das Integral von -Unendlich bis Unendlich von cosh(x)^-1 her nehme, dann kommt da Pi raus.

Aber wenn ich mich annähere mit Rechtecken unter dem Graph und ich diese immer genauer mache, müsste doch das selbe rauskommen. Oder?

Wie löst man diese Aufgabe? Vorallem stellt sich für mich die Frage, wie man die Grenzen des Integrals hier herausfinden soll...

Kann mir jemand bei dieser Aufgabe helfen?

 g(x) = tan(x), gesucht ist die Stammfunktion G(x).

Ich weiß leider nicht, wie ich vorangehen soll.

Danke schonmal im Vorraus. Stern bekommt ihr dann, wenn ichs vergeben kann.

LG

Ich verstehe bei der d) leider nicht wie ich das rechnen soll. Ich habe versucht F(7)-F(-4) auszurechnen, aber da kommt das Ergebnis von der c) raus :(

Könnte mir jemand helfen?

Kann mir jemand helfen die Aufgabe zu lösen? Ich verstehe die überhaupt nicht

Aufgabe 1 hab ich schon:) Bitte um Hilfe bei 2 und 3. warum gilt die Regel nicht für n=-1? Und wie mache ich die Stammfunktion bei 2&3?:)

f(x) = 2e^x + x^2 - 2x +1

f'(x) = 2e^x + 2x - 2

Ist das so richtig?

Und wie kann ich jetzt die Extrempunkte berechnen? Ich weiß nicht wie ich die Gleichung mit dem E Teil lösen soll

Wenn man zb Wurzel √x integrieren will kann man das auch als x^2/3 schreiben und dann leicht integrieren. Wie kann man es anders anschreiben wenn wurzel x von Grad 3 ist . also 3^√x

Hallo,

mich muss diese Aufgaben abgeben aber verstehe sie leider garnicht, könnt ihr mir die Lösung inklusive Lösungsweg erklären?
das wäre wirklich top!

Ich bräuchte Hilfe bei der d) :). Kann mir jemand helfen:))

Wir sollen diese Aufgaben für eine Präsentation in Mathe bearbeiten und kommen bei Aufgabe d und e nicht weiter. Wir haben es schon versucht und haben Ansätze, aber es wäre nett, wenn uns jemand die Aufgaben detaillierter mit einzelnen Rechenschritten oder guten Erklärungen beantworten kann.

Funktion:

w(t) = a • (t-60)² • t

Vielen Dank schonmal im Vorraus.😊

Hallo, ist das richtig?

Danke im Voraus

Hey,

Ich wollte fragen, ob ich hier etwas falsch gemacht habe:

f(x)= x-ln(x^2 -25)

gesucht: für welchen Intervall von x ist f(x) monoton fallend?

f'(x) hab ich bestimmt und es ist: ((x^2 -2x-25)/(x^2 -25)), und ich hab dann die Nullstellen von den Zähler bestimmt, dass ist (2+(104)^0.5)/2 und (2-(104)^0.5)/2, und im Nenner sehen wir dass x nicht gleich -5 oder 5 sein darf.

Die Definitionsmenge von f ist ja (-unendlich, -5) u (5, +unendlich)

daher sollte die Funktion nur dann monoton fallend sein, wenn x Element von (5, (2+(104)^0.5)/2 oder?

Danke im Voraus!

Kann man das Integral also den Flächeninhalt zu einer Parallelen von der x Achse berechnen? Z.B. Von f(x) = 4,5 das Integral zwischen - 2 und 3. Die Stammfunktion wäre ja hiermit 4,5x setzt man nun 3 und - 2 ein subtrahiert daraufhin das ergebniss von der eingesetzten - 2 vom ergebniss der - 3 ergibt sich 24,5 als Flächeninhalt. Zeichne ich aber den Graphen in ein xy koordinatensysteme und zähle die kästchen kommt 25 raus. Danke im Vorraus

Hallo alle zusammen,

ich verstehe diese Aufgabe nicht. GTR steht für Grafikfähiger Taschenrechner. Kann mir jemand bitte diese Aufgabe erklären?

freundliche Grüße

Wie wäre die aufleitung von e^2x?

Aufgabe:

27*√8 -6*√8

Ich komme auf 21√8

Was richtig ist in Lösungen gibt aber auch folgendes Ergebnis : 42 √2

Beides selbe Ergebnis aber wie komme ich auf die 2 Lösung?

Hallo 😊

Wie kann man die Aufgabe 1b) als Integral schreiben?

Weil man hat ja keine Funktion gegeben.

Danke:))

Was ist bei denen jeweils die Stammfunktion?

Hallo 😊

Was ist mit dem Näherungswert eines Integrals gemeint. Was sagt das Wort *Näherungswert* aus.

Ich meine, mit einem integral reche ich ja die exakte Fläche aus.

Danke

Ich schreibe morgen eine Mathe-Arbeit und rechne gerade Übungsaufgaben. Jetzt soll ich hier eine Fläche berechnen, diese ist von der Funktion f, der y-Achse und der Geraden y=2 eingeschlossen.

Sprich die Pinke Fläche auf dem Bild:

In der Lösung steht:

Wie komme ich vor allem auf diese 4 von der f(x) abgezogen wird? Das verstehe ich nicht

~ Schulbuch Mathematik (Bild oben) ist vom Klett-Verlag

Eine ganzrationale Funktion 3. Grades ist punktsymmetrisch zum Ursprung, hat ein Maximum bei x=√3 und schließt im ersten Quadranten mit der x-Achse eine Fläche mit dem Inhalt 9/4 FE ein. Um welche Funktion handelt es sich?

Hey, komme bei der Aufgabe nicht weiter also die Stammfunktion wäre F(t)=9t-1/300t^2 auch für die Bedingung F(0)=0 wäre das erfüllt. Aber bei der b) steht gebe an dass der Heizkessel nach 30 min leergelaufen ist und und da verstehe ich nicht wie man vorgehen soll und auch bei dem Punkt wo man berechnen soll, wie viel Wasser sich zu Beginn darin befunden hat, weil wir hatten doch gesagt F(0)=0

Danke im Voraus

Bspw. f(x)=x hoch -1 oder g(x)=x hoch -2

hallo, kann mir einer weiterhelfen?

Gegeben ist die Gleichung: ∫ (2𝑥 − 6) 𝑑𝑥 = −9 .

Obere Grenze: k

untere Grenze: -2

a) Berechnen Sie 𝑘.

In den Lösungen steht 𝑘1 = 7; 𝑘2 = −1 ich weiß leider nur nicht wie man darauf kommt.

b) Erläutern Sie auch anhand geeigneter Ergänzungen der vorgegebenen Zeichnung im Material, dass es zwei Lösungen dieser Gleichung geben muss.

Woher stammt bei der Aufgabe 13b die 4 und warum wird das integral mit 2 multipliziert?

ich bin etwas verwirrt, da man ja sonst eine funktion hat und dann die in die formel der integral einsetzen kann mit dem mal pi davor natürlch aber jetzt sind 2 funktionen gegeben und mir fehlt der ansatz bitte helfen

Nur 7 A

Hallo ich habe folgendes Problem, nähmlich, dass ich nicht weiß wie ich diese Gleichung nach a auflösen kann.

Lösung soll a=0.5 sein, kann es aber nicht schriftlich, da ich nicht weiß, wie ich vorgehen soll.

Ein Rechenweg wäre super zum nachvollziehen und verstehen

Lg

Niklas

Die Lösung soll a=0.5 zu dem Flächeninhalt 2/3 sein.

Ich komme leider nicht auf a, da ich nicht weis wie ich es von hier aus ableiten soll.

Ein Rechenweg wäre Gold wert.

Lg Niklas

Moin, könnte mir einer weiterhelfen bei Aufgabe 15/ (c).

Ich habe es hinbekommen die Schnittstellen zu finden, doch komme in Schwierigkeiten, wenn es um die Gleichsetztung und demnach findung des Parameters a geht.

Ich würde mich sehr freuen, wenn du meine Gleichung mal anschauen kannst und mir evtl. den Lösungsweg zum lösen dieses Systems zeigen könntest

Lg Niklas

Kann mir jemand Integralrechnung erklären?Am besten so, dass es sogar ein 8/9 Klässler verstehen würde.

Ich habe Probleme bei der Aufgabe:

(2/3 soll zweidrittel sein)

Der Wert zum Einsetzen am Ende ist x= -0,5

f(x)= 12x^2 - 4/3x + 7

f(x)= 12*(-0,5)^2 - 4/3(-0,5) + 7

=32/3 ist das Ergebnis

Eigentlich muss das Ergebnis 10 (2/3) sein

Bei starkem Regen können Bäche gefährlich anschwellen. Um Schäden zu verhindern, leitet man über die Kanalisation aufgefangenes Regenwasser in oberirdische oder unterirdische Rückhaltebecken. Ist nach dem Regen der Wasserstand in den Bächen wieder auf das normale Niveau gefallen, kann man das Rückhaltebecken entleeren. Ein leeres Rückhaltebecken wird zunächst 20 min mit einer Zuflussgeschwindigkeit von 20 m^3/min geflutet. Nach weiteren 10 min wird es wieder entleert. Durch den Abfluss fließen 30 m^3/min.

a) stellen Sie die Zufluss – beziehungsweise Abflussgeschwindigkeit (in m^3/min) in einem Koordinatensystem in Abhängigkeit von der Zeit (in min) dar.

b)Berechnen Sie die Wassermenge im Becken nach 10 min, 20 min… 50 min.

c) Erstellen Sie ein Funktionsterm, mit dem man die Wassermenge im Becken in Abhängigkeit von der Zeit berechnen kann. Zeichnen Sie auch den Graphe dieser Funktion.

d) Der Graph, der die Zufluss – bzw. Abflussgeschwindigkeit darstellt, schließt mit der x–Achse zwei Rechtecke ein. Deuten Sie deren Flächeninhalt im gegebenen Kontext.

Ich bräuchte dringend Hilfe bei diesen Aufgaben. Wir haben das Thema Integralrechnung jetzt erst neu in Mathe angefangen und ich verstehe es nicht wirklich. Mir fehlt da irgendwie der Ansatz und ich weiß nicht so richtig wie ich anfangen soll. Kann mir da jemand helfen?

Ich habe zuerst die drei Integrale von 0 bis 24 gebildet.

Dann habe ich die Abflussrate von der Zuflussrate abgezogen. Anschließend die zusätzliche Zuflussrate durch den Regen mit dazu multipliziert

Ist das korrekt?

Warum ist meine Rechnung falsch, ich verstehe das nicht. In der Muster Lösung hat man anfangs nur für den e Teil eingesetzt aber 1 nicht. Der Rest von Teil aber wird normal integriert mit dem Hauptsatz der Differenzial und Integralrechnung.

Musterlösung

ich brauche dringend hilfe. bei b unc c

hey Leute,.

ich komme bei a und b nicht weiter

ich denke die ersten 50 km werden so berechnen

A1 =15*50=750 dort steht nämlich die ersten 50 km und ich weiss nicht ob ich die formel für ein trapez verwenden soll oder für ein rechteck weil bis 30 kmh sieht es aus wie ein rechteck 😐

für Unterstützungen wäre ich dankbar

Siehe Bild. Wie bilde ich hier die Stammfunktion? Wie muss ich vorgehen? Welche Regel gilt hier?

Mit partieller Integration und/oder Substitution bin ich nicht weiter gekommen.

Hallo, hoffe ich kann das alles gut ausdrücken:

1.Wie berechnet man genau das Integral von zB

[0,b], [a, 10] oder [a,b] irgendeiner Funktion f -> f(x)dx (bei zwei Zahlen weiß ich wie das geht)?

Ich gehe davon aus, das zB bei [a,10] wird am Ende eine Art Formel rauskommen wird, In der man dann für den Parameter a eine beliebige reelle Zahl eingeben kann und so direkt den Flächeninhalt bekommt? Kann mir das jemand vllt für f(x) = 2x^3-5x^2+6x+2 ausrechnen?

2.Wenn 2 Funktionen f und g innerhalb von [a,b] eine Fläche oberhalb der x-Achse einrahmen, muss ich die Funktionen dann addieren oder subtrahieren? Das gleiche gilt, wenn f und g unterhalb der x-Achse eine Fläche einrahmen, + oder -?

3.Sagen wir Funktion f und g rahmen von [a,b] eine Fläche unterhalb der x-Achse ein und von [b,c] oberhalb der x-Achse und ich will wissen, wie die Fläche von [a,c] ist, berechne ich dann einfach die Schnittpunkte von f und g, nehme die als Grenzen? Aber dann wieder addieren oder subtrahieren?

Vielen lieben Dank!

Ich bin total verzweifelt bei der Aufgabe c.). Wie berechnet man dort den Integral?

Danke im Voraus

Ich komme hier nicht weiter. Siehe Bild muss ich berechnen, in welchem Bereich das Logo mindestens 25 cm, also 2.5dm hoch ist.

Die obere f(x) = -0.125x² +2

Die untere g(x) = 0.1875x² -3

(Fläche A = 26.666 dm²)

Was soll ich da am besten machen um den Abstand von25 rauszubekommen?

Danke im Voraus

Frage steht da :)

Hallo!

Ich würde gerne die Gammafunktion lernen. Aber dafür muss ich wissen, wie man von 0 bis unendlich integriert. Wie macht man das?

Die Gammafunktion lautet ja: Γ(x) = (Integral von 0 bis unendlich) t^(x-1)*e^(-t) dt

Aber wie integriere ich das von 0 bis unendlich?

Angenommen, Ich würde das machen:

∞^(x-1)*e^(-x) - 0^(x-1)*e^(0) = ∞^(x-1)*e^(-x) - 1 =? ∞ - 1 = ∞

Das würde heißen, dass x! = ∞. Aber das stimmt offensichtlich nicht:

1! = 1

2! = 2*1 = 2

3! = 3*2*1 = 6

4!=4*3*2*1=24

...

Wie integriere ich von 0 bis ∞?

Ich verstehe nicht, wieso hier zwei Lösungen rauskommen:

Bitte um Hilfe :)

Ich verstehe nicht ganz, was der Hauptsatz der Differential- und Integralrechnung aussagt.

Wodurch verbinden sich Integral- und Differentialrechnung?

Ich weis das hier ist mathematisch nicht korrekt aufgeschrieben aber mir gehts ums Prinzip. Eigentlich soll die Flächenbilanz null ergeben aber kann man auch die Grenzen umändern, sodass die beiden Flächenanteile positiv sind. In der Sunne ergibt die Fläche zwar null aber wenn ich die beiden in zweierlei Intervallen addiere dann kann man doch auch 0,5 FE Schreiben?

Hallo,

Jetzt muss ich schon wieder wegen einer Aufgabe, um Hilfe bitten. Aber da ich im Internet nur das Beispiel, ohne die Aufgabenstellung die ich bräuchte fand, muss ich jetzt doch fragen.

Aufgabe 1), 2) und 3) habe ich geschafft, aber ich komme nicht auf das Ergebnis für 4). Die Funktionsgleichung ist übrigens: x^2/8

Könntet ihr mir vielleicht den Lösungsweg für die Aufgabe 4) schreiben?
Die Lösung sollte übrigens 1,206m sein.

Guten Abend,

Ich sitze gerade an einem Beispiel dran, wo ich schon seit einer gewissen Zeit nicht mehr weiterkomme.

Das Problem ist vorallem, dass wir uneigentliche Integrale noch nicht besprochen haben, weshalb es schwierig ist dieses Beispiel zu Rechnen.

Könnte mir jemand die Lösung mit Lösungsweg bitte berechnen?
Die Lösung sollte für 1) 7dm2 sein und für 2) 151,9 kg.

A)

Wie kann ich das Volumen mit Dreifachintegralen bestimmen?

Hallo,

ich hänge sehr lange an der Aufgabe und komme leider nicht voran.

in den kurzlösungen steht, dass das ganze 1/4 ergibt, nur leider komme ich nicht zum richtigen Ergebnis:(

(Habe sowohl sin als auch cos substituiert…)

Ich würde mich freuen, wenn ihr mir weiterhelfen könntet.

danke im voraus :)

Hallo, wie kommt man bei Aufgabe c) auf g(x) ?? Wir haben doch nur die Funktion f(x) gegeben??

hi,

kann mir jemand sagen wie ich dieses integral lösen kann?

ich dachte vielleicht an Substitution, dann könnte ich x^3 substituieren aber ich denke ich kann dann schlecht etwas Wegkürzen?

dann doch partielle Integration, aber wie wähle ich hier dann mein u und v'?

ein tipp würde mir sehr weiter helfen!

danke !

Die folgende Aufgabe veranschaulicht, wie ein Integral funktioniert.

Die obere und untere Grenze wird in die Stammfunktion eingesetzt und deren Funktionswerte werden voneinander abgezogen:

F(5)-F(1) = -1,33-1,66 = -3

Aber warum funktioniert das? Was sagt die Stammfunktion überhaupt aus?

Hey kann mir einer erläutern wie ich zum Ergebnis von b komme? Also oben ist die Aufgabe und unten die Lösung.
schonmal danke

Hallo

Wie berechnet man dieses Beispiel?

Moin, hat jemand einen Ansatz für die Aufgabe?

Hallo. Ich hab eine Aufgabe von einer Mathe Prüfung von dem Teil ohne Taschenrechner. Es ist eine Aufgabe mit Integral. Den einzigen Part den ich nicht verstehe ist, wie man (2•π/4) im Kopf rechnen soll. Es kommt (π/2) raus. Kann mir das jemand erklären?

Hey, ich habe die Aufgabe als Hausaufgabe:

Habe jetzt echt lang probiert einen Ansatz zu finden und das ist alles was ich hab:

Ich komme jedoch nicht weiter und brauche ehrlich hilfe..

Mir ist klar:

sin(x) / cos(x) = tan(x), aber wie soll man von dem Bruch bei dem Pfeil mit der 1 auf 1/cos^2(x) kommen und von da auf 1+ tan^2(x)?

Guten Abend,

kann mir jemand bei dieser Aufgabe kurz weiterhelfen?

Muss ich hier nur die Fläche im ersten Quadranten der Parabel sowie einmal der grauen Fläche (das kleine Stück oben an der nach unten geöffneten Parabel) berechnen und dann das Verhältnis berechnen? Oder muss ich von einer runden Wurfscheibe ausgehen und alle Werte *2 multiplizieren?

Es ist ja die Rede von einem Parabelstück, dass um die x-Achse rotiert. Dann müsste es ja auch nach unten rotieren?

Die Aufgabe lautet:

Das ist die bearbeitete Aufgabe:

Laut Lösung muss u = 6 sein.

Guten Abend, 🌇

kann mir jemand bei der folgenden Aufgabe vielleicht weiterhelfen?

Ich komme hier leider nicht weiter…

Gerne zu a) b) und c) die einzelnen Schritte posten, die es zur Lösung braucht. 😄

Hello :)

Also zu diesem Thema weiß ich, dass eine Fläche oberhalb der x-Achse positiv ist, unterhalb negativ und wenn zwei gleich große Stücke ober- und unterhalb sind, das Integral Null ist.

Wie sieht es aber aus mit einer Fläche zwischen zwei Funktionen?

Ändert es was, wenn sie ober-/unterhalb der x-Achse ist oder einfach inmitten der x-Achse (also unten und oben)?

Also es geht hier darum, dass man anhand der Funktion und einer Skizze bestimmen soll, wie das Integral ausfällt. Keine Rechnung.

Help :(

Ich habe zwei Aufgaben gegeben:

1)Betrachten Sie das Intervall 𝑰 = [−𝟑; 𝟒]. Berechnen Sie die Flächenbilanz über dem gegebenen Intervall. Interpretieren Sie die Bedeutung Ihres Ergebnisses mathematisch. 

2)Berechnen Sie die Fläche, die die Funktion mit der x-Achse einschließt. Berechnen Sie zunächst geeignete Intervalle zur Flächenaufteilung. 

Ich habe die 1) so berechnet:

Bei der 2 habe ich mit Satz des Nullprodukts und PQ-Formel

3 Nullstellen bestimmt

x=0

x1=-3

x2=4

Ich könnte jetzt wieder die Stammfunktion berechnen und anschließend den Flächeninhalt berechnen. Das würde doch dann aber wieder auf Aufgabe 1 hinaus laufen.

Wo liegt der Unterschied zur Aufgabe 1 und 2?

Hallo, ich habe die Möglichkeit meine Note zu verbessern und kann diese 2 Aufgaben erledigen, jedoch kann ich Mathe absolut nicht und bin daher sehr verzweifelt. Ich brauch diese Note, da ich zurzeit mein Abi mache und das beste rausholen möchte.

Kennt sich jemand damit aus und kann mit weiterhelfen?

kann jemand mir eine ausführliche Erklärung geben ? Denn das ist doch Integralrechnung oder nicht ??

Hey,

In Mathe haben wir das Thema Integralrechnungen. Leider verstehe ich nichts. Wie berechne ich soetwas?