Wie berechne ich hier die Fläche?

Die Aufgabe ist:

Berechne mit Hilfe von F den Inhalt der Fläche, die von f mit den koordinatenachsen und der Geraden mit der Gleichung x = 10 eingeschlossen wird.

f=10x*e^-1/2x

F=-20(x+2)e^-1/2x

Kann mir jemand den Ansatz geben, wie ich hier integrieren muss und wie ich die Gerade x=10 einbringen muss?

Answer 1

[Halbrecht]

x = 10 ist eine Senkrechte , die durch (10/0) geht

.

Mit Skizze im GTR ist sofort klar ,dass das Int von 0 bis 10 geht .

.

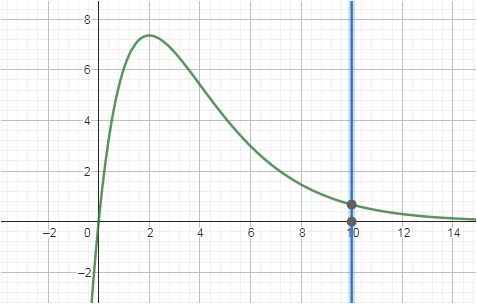
Ohne Skizze muss man feststellen , ob zwischen 0 und 10 eine Nullstelle ist .

da bei f(x) =10x MAL e^(-1/2x) nur x = 0 als NST infrage kommt , ist klar 

InT von 0 bis 10 

-20(10+2) * e^(-0.5*10) ist zu berechnen 

Answer 2

[Wechselfreund]

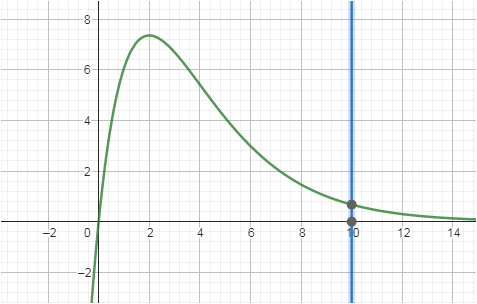
f hat eine Nullstelle bei x = 0. Du musst also von 0 bis 10 integrieren, wobei ja eine Stammfunktion gegeben ist.

Answer 3

[gauss58]

Bei x = 0 ist eine Nullstelle. Die obere Integrationsgrenze des Integrals ist x = 10. Somit bestimmst Du das Integral in diesen Grenzen.