Integral einer gesuchten Fläche?
Ges.: Inhalt der grau markierten Fläche berechnen

Lösung

Aber wenn ich die ''box'' (3 mal 2.25) minus 1. Fläche mache bleibt doch die box ohne 1. über. Gesucht ist die graue Fläche, wie kann das sein

3 Antworten
Nein. Keine Ahnung, wie Da drauf kommst: Die weiße Fläche unterhalb des Graphen der Funktion g(x) ist

Wenn man diese Fläche vom Rechteck abzieht, bleibt die graue Fläche als Rest übrig.

Du rechnest das Rechteck, also 2,25 * 3 minus der Fläche unter der Kurve g, das ist das Integral von 0 bis 3. Das ergibt die gesuchte Fläche.
Jein. Der Betrag des Integrals ist die vom Graphen und der x-Achse eingeschlossen Fläche. Dies wird extrem wichtig, wenn Du eine Fläche berechnen sollst, die Funktion aber innerhalb zu berechnenden Intervalls eine oder mehrere Nullstellen hat, denn das Integral eines unterhalb der x-Achse verlaufenden Graphen einer Funktion ist negativ. Merke daher: Integral und Fläche sind unterschiedliche Dinge.
Was ist jetzt der Unterschied zwischen eine Fläche und Integral?
Es gibt keine negative Fläche weshalb das Integral im Minus Bereich mit Betrag geschrieben wird, das weiß ich
weshalb das Integral im Minus Bereich mit Betrag geschrieben wird, das weiß ich
Dann sollte Dir ja klar sein, was der Unterschied ist. Weil es eben einen Unterschied gibt, muss man das Integral in Betragsstriche schreiben, wenn man eine Fläche berechnen will. Wäre Integral und Fläche identisch, dann bräuchte es ja keine Betragsstriche (Rechne mal Integral von x³ im Intervall [-1;1] und dann die Fläche, die vom Graphen und der x-Achse eingeschlossen wird)
Die Integralrechnung ist weit mehr als die in der Schule nahegelegte (sehr bedenkliche) Gleichsetzung von Integralrechnung mit Flächenberechnung, von der man sich dann, wenn man ein technisches Studium beginnen sollte, erst mühsam wieder lösen muss. Die Berechnung von Flächen ist eine Anwendung der Integralrechnung, aber bei Weitem nicht dasselbe.
Was ist jetzt der Unterschied zwischen eine Fläche und Integral?

integral von -2 bis +2 = Null
Fläche wäre die tatsächlich sichtbare. erhält man natürlich durch 2 * int (-2 bis 0 ) oder 0 bis +2
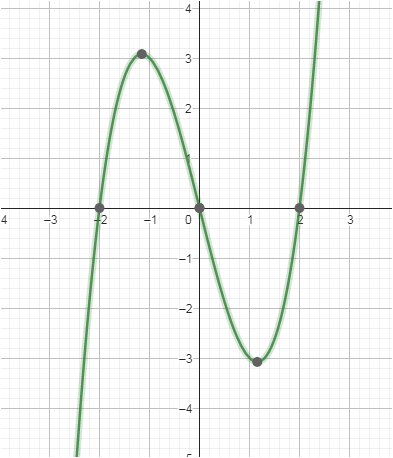
integral ist also die Fläche unter der Funktion bis zur x achse, okay