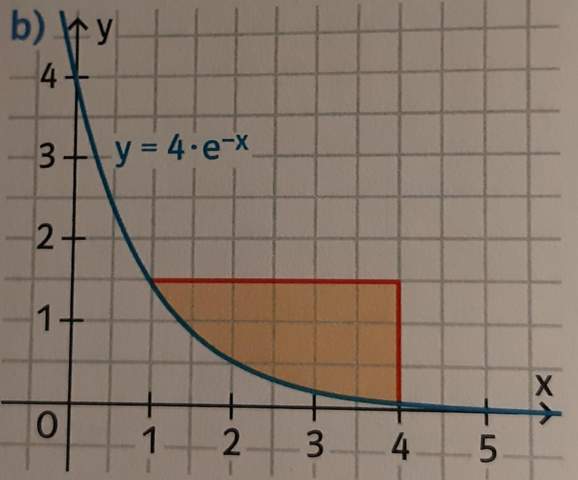
Gefärbte Fläche Inhalt berechnen?
Wie berechne ich den Inhalt der gefärbte Fläche?
Einfach das Integral von 1 bis 4 oder muss ich etwas beachten?
3 Antworten
oder muss ich etwas beachten?
dass Integrale nicht für Flächen oberhalb der Kurve geeignet sind
schau : vom Rechteck mit Fläche 3*1.5 wird die Fläche unter der Kurve abgezogen
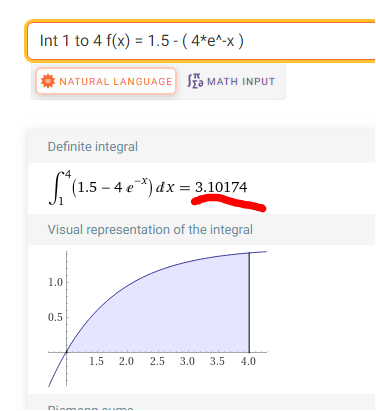
Int 1 to 4 f(x) = 4*e^-x = ca 1.39 ( was man auch erkennen kann , bedenke 4 Karos = 1 Flächeneinheit FE
daher ist orange 4.5 - 1.39 = ca ??? FE groß
.
Ohne REck würde man
Int 1 to 4 f(x) 1.5 - ( 4*e^-x ) bestimmen , was zum selben
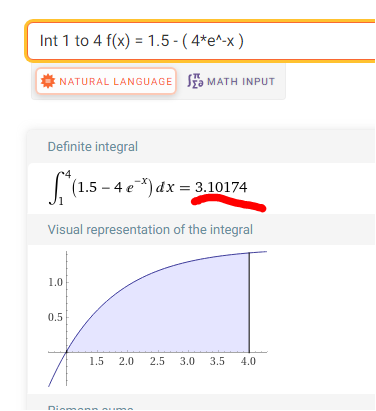
ergebnis kommt .
Eine Alternative zu gauss58-Antwort: Wir drehen die Funktion um
y_1 = -4e^(-x)
und jetzt verschieben wir sie um 1 nach links, also y_2 = -4e^(-x-1)
und nun das ganze um 1,5 nach oben, also y_3 = -4e^(-1-x) + 1,5 = -4e*e^(-x) +1,5
Y-3 = 4e^(1-x) + 1,5x
und davon bilden wir das Integral von 0 bis 3
für 0 bis 3: 4e^(-4) + 4,5 - 4e
Aber besser so wie gauss58: 4,5 - |4e^-x|für(1 bis 4) = 4,5 - 4e + 4e^(-4), dasselbe
Rechteck minus Integral in den Grenzen von 1 bis 4
Mit dem Integral berechnest Du die Fläche unter der Kurve bis zur x-Achse in den Grenzen von 1 bis 4. Das ist aber nicht die gesuchte Fläche, sondern die Fläche, die Du von dem Rechteck in den Grenzen von 1 bis 4 und der Höhe 1,5 abziehen musst. Also A_Rechteck = (4 - 1) * 1,5 = 4,5.
Das Integral berechnet die Fläche unter der Kurve, die gefärbte Fläche ist aber oberhalb der Kurve,
Um sie zu bekommen, musst du daher zuerst die Fläche des (mit etwas Fantasie leicht erkennbaren) 3 mal 1,5 Einheiten großen Rechtecks berechnen und dann von diesem das Integral (also die Fläche unter der Kurve) abziehen.
Das mit dem Rechteck abziehen hatten wir noch nicht, was meinst du damit?