Inhalt der Fläche berechnen, Integrale?

Berechnen Sie den Inhalt der Fläche, die vom Graphen f und der Tangente in P und der x-Achse begrenzt wird.

f(x)=e^x -1 P(ln(5),4)

Bis jetzt habe ich die Tangentengleichung t(x)=5x-4,05 berechnet. Aber wie rechnet man nun weiter

Answer 1

[Applwind]

Deine Tangentengleichung ist leider falsch.

Sie müsste y = 5(x-ln(5)) + 4 lauten oder meinetwegen y = 5x - 5ln(5)+4, denn

y(ln(5)) = 5*ln(5) - 5ln(5) + 4 = 4 = f(4)

aber y(ln(5)) = 5ln(5)-4,05 ≠ 4

Woher ich das weiß: Hobby – Schüler.

Comments

[Halbrecht]

 y = 5x - 5ln(5)+4........ist gerundet -4.05

[Applwind]

@Halbrecht

Stimmt. Ich plädiere trotzdem immer ungerundete Werte zu verwenden.

[Halbrecht]

@Applwind

richtig .Aber ich finde , deine Formulierung macht den Eindruck er läge ganz falsch.

.

In der Tat ist erst mit 4 - ln(5) erreichbar , dass Gerade und f(x) nur einen Punkt gemeinsam haben . mit -4.05 gibt es zwei

[lien343]

Danke für den Hinweis! Und wie rechne ich jetzt weiter mit den Integralen?...

[Applwind]

@lien343

Du integrierst von null bis zur Nullstelle der Tangente(die musst du natürlich noch ausrechnen).

Answer 2

[Halbrecht]

ich erhalte auch die Werte deiner Tangentenglg.

f'(x) = e^x 

f'(ln(5)) = 5

.

4 = 5*ln(5) + b 

4-5*ln(5) = b = -4.0472

.

y = 5x - 4.0472 

.

skizze machen

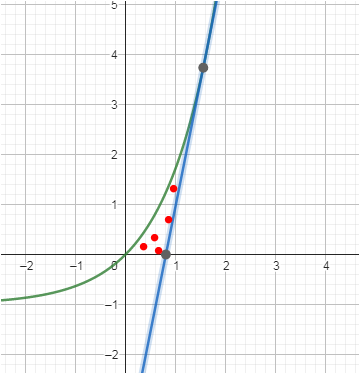
Schnittpunkt ist schon berechnet : ln(5)

Integral 0 to ln(5) f(x) = e^x - 1 - ( 5x - 4.05) .............Wert zwischen 2 und 3

.

wirklich exakt wird es erst mit 4-ln(5) für b , aber 4.047189562170 hilft auch.

.

Nochmal wegen Genauigkeit : mit 5x - 4.05 = e^x - 1 würde man feststellen ,dass es gar keine Tangente ist , denn diese Glg hat zwei Lösungen

Comments

[lien343]

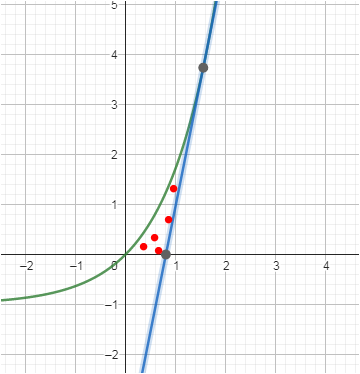
Ich habe es mal gerechnet und habe 2,43 FE raus mit der Tangente t(x)=5x-4,05 .. stimmt das? und welche Tangentengleichung soll ich jetzt benutzen, welche ist besser...

[Halbrecht]

@lien343

stimmt . Besser ist ist natürlich 5 - 4*ln(5) , nur der Wert ist exakt . Kann sein, dass du die Syntax im TR ( oder womit rechnest du ? ) nicht hinkrist oder der TR keine Grenzen in dieser Form akzeptiert.