Inhalt einer Fläche Graph und Tangente?
Berechne den Inhalt der Fläche, die vom Graphen von f, der Tangente im Punkt P und der x-Achse begrenzt wird.
a) f(x)=e-x-1 ; P(2;f(2))
Wie gehe ich hier vor?
Sicher x-Achse oder doch y-Achse?
In der Aufgabenstellung stand x-Achse
2 Antworten
Tangente:
t=m x + b
m ist die Steigung also die erste Ableitung der Funktion an der Stelle x ist 2
b erhältst du dann indem du den Punkt(2;f(2)) in die Gleichung der Tangente einsetzt
Der Fläche rechts von der y-Achse erhältst du:
Integral von 0 bis 2 über f(x) - t(x) dx
Wenn die Fläche wirklich von der x-Achse begrenzt ist dann musst du noch links von der Y-Achse die Dreiecksfläche berechnen(mach dir eine Skizze, dann kann man leicht verstehen, was ich meine)
Berechne die Tangente im Punkt p. Berechne das Integral von 0 bis 2 von f(x) und multipliziere mit -1 (Fläche F). Berechne den Schnittpunkt x0 der Tangente mit der x-Achse. Berechne die Dreiecksfläche D des Dreiecks von x0 bis 2. Berechne D - F, fertig.
Wenn du die Tangente korrekt berechnet hast, kannst du dir den Verlauf von f und der Tangente hier
https://rechneronline.de/funktionsgraphen/
anschauen. Das sollte dir ein wenig Orientierung geben.
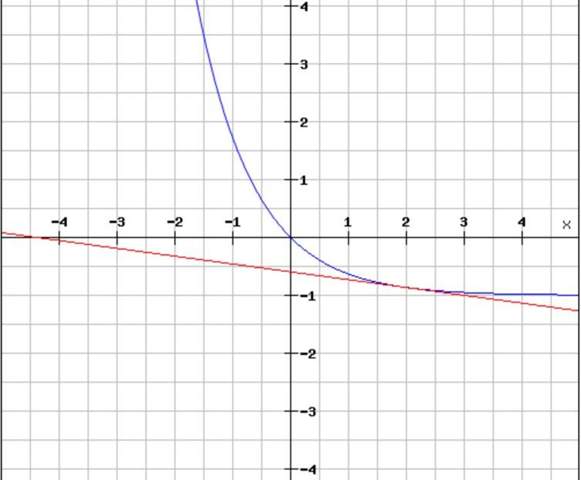
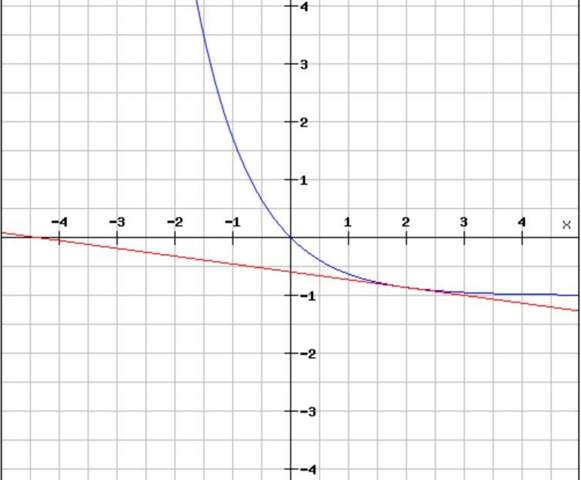
(2, f(2))!