Wie löse ich folgende Mathe-Aufgabe?
Der Graph der Funktion f mit f(x) = 4 - x² schließt mit der x-Achse eine Fläche ein. Gib deren Größe an. Es wird an der Stelle x = -1 die Tangente an den Graphen von f gelegt. Berechne den Inhalt der Fläche im II. Quadranten, die vollständig begrenzt wird von der Tangente, dem Graphen von f sowie Teilen der x- und y-Achse.
Vielen Dank im Voraus!
3 Antworten
Berechne den Inhalt der Fläche im II. Quadranten, die vollständig begrenzt wird von der Tangente, dem Graphen von f sowie Teilen der x- und y-Achse.
Der Flächeninhalt von 6,25 ergibt sich wenn die Tangente von -2,5 bis 0 abgefahren wird.
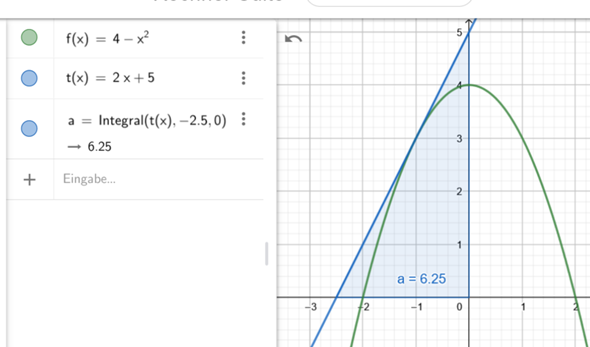
Der Flächeninhalt von 16/3=5,33 ergibt sich wenn die Funktion f(x) von -2 bis 0 abgefahren wird.
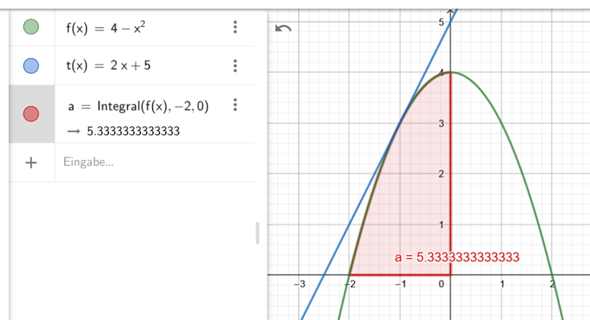
Das war ja das was in den Lösungen stand.
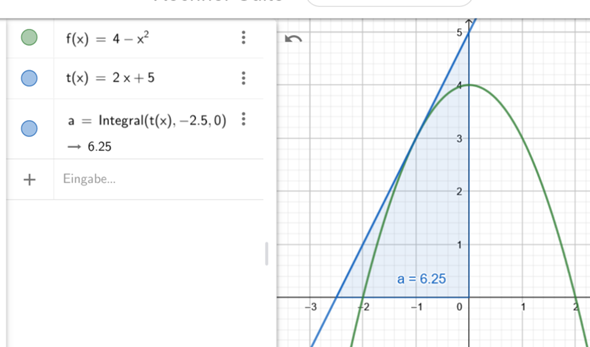
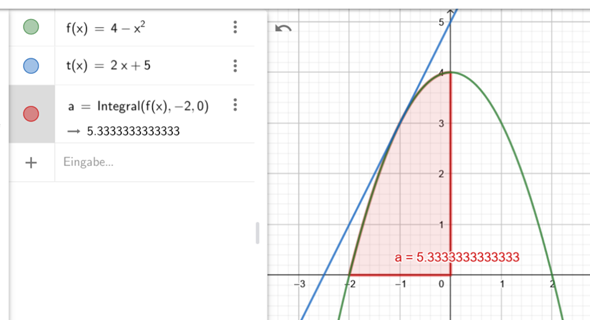
Integrieren von linker bis rechter Nullstelle.
.
f(-1) und f'(-1) bestimmen.
Damit die Tangentengleichung erhalten.
.
3 = 2*-1 + b
5 = b
t(x) = 2x + 5
.
Dann Nullstelle von t(x ) bestimmen und wieder integrieren t(x) - f(x) von Nullstelle bis x = 0
.
Alternativ kann man die Dreiecksfläche mit 5 * 2.5/2 bestimmen und davon die Hälfte der Fläche von a) abziehen
.
so sieht das aus
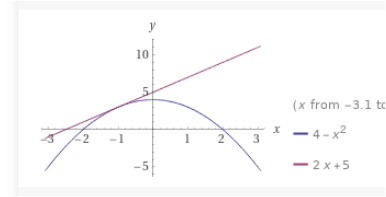
das sind die Flächen
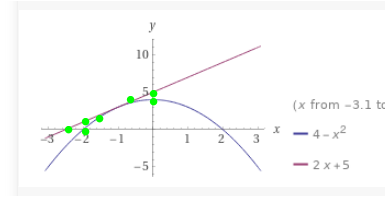
Links, ab Schnittpunkt rot mit der x-Achse.
Bis rot und blau zusammentreffen.
Dann blau bis zur y-Achse.
Du brauchst für den ersten Teil:
- Nullstellen von f(x)
- Stammfunktion F(x) zu f(x)
- Berechne F(xn2) - F(xn1), wobei xn1 und xn2 die Nullstellen sind.
Im zweiten Teil muss du noch eine Fallunterscheidung einbauen.
a) von xn1 bis -1 mit der Geraden ( = Tangente )
b) von -1 bis 0 mit f(x)
genau, das habe ich verstanden, aber wie geht der 2. Teil?
Habe ich zugefügt, aber nur knapp beschrieben. Reicht das oder brauchst du noch mehr Hilfe?
Wäre sehr freundlich, wenn ich mehr Hilfe bekommen würde!
Die Tangente ist mit einem Punkt und der Steigung eindeutig festgelegt.
Der Punkt ist ( -1 | f( -1 ) ). Die Steigung ist f'( -1 ).
Damit ist die Tangente bestimmt. y = m x + b. m ist die Steigung von eben.
f( -1 ) = f'( -1 ) x + b. Nun b berechnen.
Dann die Stammfunktion der Tangente berechnen und die Fläche wie oben berechnen im Interval von [linke Nullstelle, -1].
Der zweite Abschnitt geht wie der erste Teil ganz oben, nur dass der Bereich [-1, 0] als Grenzen genommen wird.
Ich habe jetzt A = 4,1 FE raus.. stimmt, das?
Warum wird beim zweiten Abschnitt der Bereich [-1, 0] als Grenze genommen und nicht [-2, 0]?
Ich habe 10,667 raus. F(x) = 4x -x³/3.
F(-2) = -8 + 8/3; F(2) = 8 - 8/3
Fehler kann auch bei mir liegen, aber 4,1 halte ich für zu klein
Das lese ich aus der Aufgabe: Berechne den Inhalt der Fläche im II. Quadranten, die vollständig begrenzt wird von der Tangente, dem Graphen von f sowie Teilen der x- und y-Achse.
II. Quadrant ist oben links. Dann wie in meinem Kommentar zu deinem zur Antwort von Halbrecht
Also ich habe ∫2x + 5 (untere Grenze: -2,5 & obere Grenze -1) = 9/4 raus
und bei ∫4 - x² (untere Grenze -1 & obere Grenze 0) = 11/3
Grenzen der Tangente sind richtig. Hatte das übersehen.
Nur Tangente: t(x) = 2x + 5. T(x) = x² + 5x.
T(-2,5) = 6,25 - 12,5 = -6,25.
T(-1) = 1 - 5 = -4
T(-1) - F(-2,5) = +9/4, wie du auch.
Nun von oben:
F(x) = 4x -x³/3
F(-1) = -4 + 1/3 =
F(0) = 0
F(0) - F(-1) = 11/3, wie du auch
Also in den Lösungen steht A = 6,25 - 16/3 = 0,917 (FE)
Irgendwie:
A1 = 2∫(4 - x²) dx (obere Grenze 2 & untere Grenze 0) = 32/3
Ad = (2,5 * 5) / 2 = 6,25
Ap = 16 /3
Könntest du graphisch nochmal darstellen, welche Fläche ich jetzt berechne.. wäre sehr nett..