Integralrechnung Frage Q1?
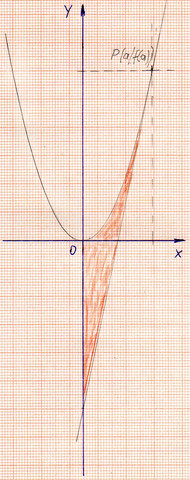
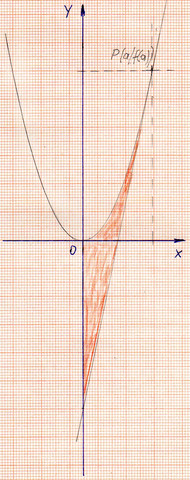
Beweisen Sie: Der Graph von f mit f(x)= x^2, die Tangente an f in P (a | f(a) und die y-Achse begrenzen eine Fläche mit dem Inhalt A= 1/3a^3
3 Antworten
siehe Mathe-Formelbuch Fläche zwischen 2 Funktionen und "Diffentialgeometrie"
1) A=integral(f(x)-g(x) Fläche zwischen 2 Funktionen
untere Grenze xu=0 und obere Grenze xo=a
2) Tangentengleichung ist yt=f´(xo)*(x-xo)+f(xo) xo ist der berührungspunkt,wo die Tangente yt =.. die Funktion f(x)=.. berührt.
f(x)=x^2 und f´(x)=2*x eingesetzt
yt=2*xo*(x-xo)+xo^2=2*xo*x-2*xo^2+xo^2
yt=2*xo*x-xo^2 eingesetzt
A=Inte. (x^2-(2*xo*x-xo^2)*dx
A= Int. (x^2-2*xo*x+xo^2)*dx
A=1/3*x^3-xo*x^2+xo^2*x+C mit xo=a und xu=0
A=1/3*a^3-a^3+a^3)-(0-0+0)
A=1/3*a^3
Hinweis : xo=a also wo die Tangente yt die Funktion f(x) berührt.
Ach ist xo=a die obere Integrationsgrenze.
Eine Tangente t(x)=mx+n an einer Funktion f(₀) an einer Stelle x0 erfüllt:
m=f'(x₀)
t(x₀)=f(x₀)
__________
Explizit gilt für t(x) hier:
m=f'(a)=2a
t(x0)=f(a)=a²
=> t(x)=2ax+a²
__________
Bestimme nun die Fläche, welche von f(x), t(x) und der y-Achse eingegrenzt wird.
siehe Mathe-Formelbuch "Differentialgeometrie"
Tangentengleichung yt=ft(x)=f´(xo)*(x-xo)+f(xo)
xo ist die Berührungsstelle.
Fläche zwischen 2 Funktionen
A= Integral(f(x)-g(x)
f(x) ist die obere Begrenzung und g(x) die untere Begrenzung
hier kann man auch über Nullstellen hinweg integrieren,weil wegen des minuszeichens -g(x) die Flächen unter der x-Achse ein "positives "Vorzeichen bekommen und somit automatisch addiert werden.
Im Normalfall darf man nicht über Nullstellen hinweg integrieren.
A=Int(x^2-((f´(xo)*(x-xo)+f(xo))*dx
xo=a und a ist auch dann die obere Integrationsgrenze (x=a)
Grafik zur Integralrechnung