Der Graph von f mit f(x)= 3x^2, die Normale an den Graph von f in P(2| 12) und die y-Achse schließen eine Fläche ein. Wie rechne ich das?
Die Fläche mit der x-Achse ist 8.
5 Antworten
siehe Mathe-Formelbuch,Differentialgeometrie
Tangentengleichung yt=ft(x)=f´(xo)*(x-xo)+f(xo)
Normalengleichung yn=fn(x)=-1/f´(xo)*(x-xo)+f(xo)
xo=Stelle,wo die Tangente/Normale liegt
f(x)=3*x² abgeleitet f´(x)=6*x mit xo=2 eingesetzt
f(xo)=f(2)=3*2²=12 und f´(xo)=f´(2)=6*2=12 eingesetzt
yn=fn(x)=-1/12*(x-2)+12=-1/12*x+2/12+12
yn=fn(x)=-1/12*x+12 1/6
Probe: f(2)=3*2²=12 und fn(2)=-1/12*2+12 1/6=-1/6+12 1/6= 12 stimt
f´(2)=6*2=12 ist mn=-1/f´(2)=-1/12 stimmt also
Schnittstellen der beiden Funktionen f(x)=yn
3*x²=-1/12*x+12 1/6 mit meinem Graphikrechner (GTR,Casio)
xu=-2,027... und xo=2
Fläche zwischen 2 Funktionen A=∫(f(x)-g(x)
f(x)=obere Begrenzung und g=untere Begrenzung
hier f(x)=fn(x)=-1/12*x+12 1/6 und g(x)=3*x²
A=∫(-1/12*x+12 1/6)-(3*x²)=∫(-1/12*x+12 1/6-3*x²)*dx)
A=-1/12*∫(x*dx)+12 1/6*∫(dx)-3*∫(x²*dx)
A(x)=-1/24*x²+12 1/6*x-1*x³+C
A(x)=-1*x³-1/24*x²+12 1/6*x+ C obere Grenze xo= 2 und untere Grenze xu=-2,027
Die Integrationskonstante C fällt bei dieser Rechnung weg.
A(x)=obere Grenze minus untere Grenze
A=(-1*2³-1/24*2²+12 1/6*2) - (-1*(-2,027)³-1/24*(-2,027)²+12 1/6*(-2,027))
A=(16 1/6) - (-16 502)
A=16 1/6+16,502=32,67 FE (Flächeneinheiten)
prüfe auf Rechen- u. Tippfehler
ist ja nur eine Nummer vor der Gleichung gestellt.
Ich denke,was eine Tangente und eine Normale ist,dass wissen die Fragesteller.
Ich weiß nicht,wie man das noch einfacher und übersichtlicher darstellen kann.
xo=Stelle,wo die Tangente/Normale liegen soll
f(x)=... und f´(x)=... dann f(xo)=... und f´(xo)=... dann einsetzen in die Formel und ausrechnen.
einfacher geht´s nich mehr.
Steht aber in meinem Mathe-Formelbuch unter dem Kapitel "Differentialgeometrie".
ist ja nur eine Nummer vor der Gleichung gestellt.
Nicht nur, in der Formel-Zeile gibt es vor allem keinen Text. Die Nummer hilft aber auch, man kann nämlich später darauf Bezug nehmen.
Das Wichtigste dabei ist, dass die Formeln sich nicht im Text knubbeln und möglichst nicht dabei auch noch über mehrere Zeilen gehen.
Ich denke,was eine Tangente und eine Normale ist, das wissen die Fragesteller.
Das glaube ich auch. Du musst dies auch nicht so ausformulieren wie ich das tun würde.
Das Absetzen der Formeln entzerrt jedoch die Antwort deutlich. Ich habe beiderlei schon gelesen: Gut abgesetzte und aufgelockerte Texte, wo nur ganz kurze Formeln wie 'r=0' oder so im Fließtext standen, und solche, in denen alles in Fließtext stand; Letztere hab' ich gehasst.
Es ist wie ein Teig, der nicht aufgegangen ist - schwere Kost.
Hallo DarkSoul1234567,
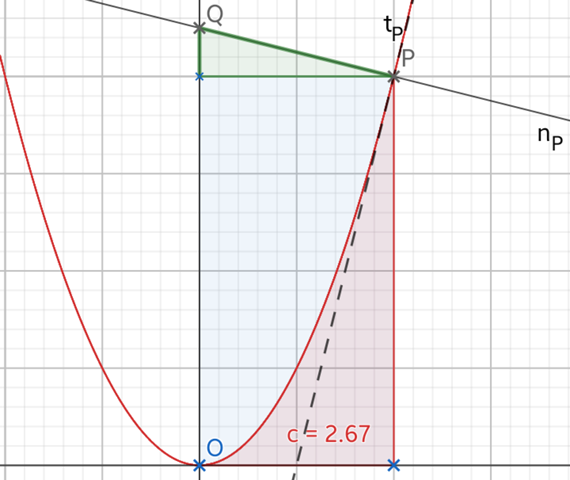
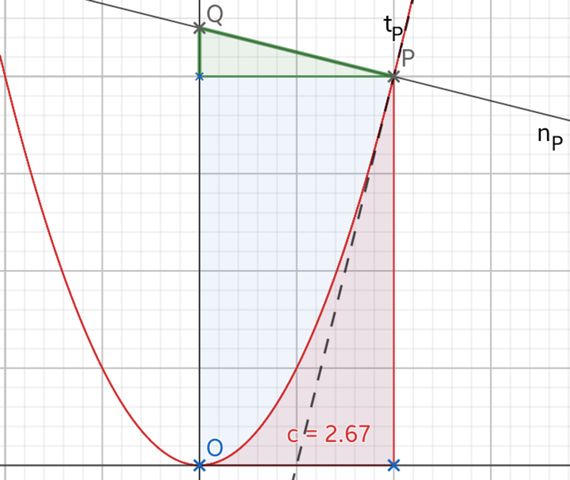
der Ursprung O und der Punkt P sind zwei Ecken eines Rechtecks x(P)×y(P), in diesem Fall
(1) A0 = 2·12 = 24.
Davon musst Du die Fläche unter dem Graphen von f(x) von x(O)=0 bis x(P)=2 wieder abziehen.
Dass diese 8 ist, hast Du selbst schon geschrieben. Darauf kommt man, durch Integration von x(O) bis x(P):
(2.1) A–= ∫x(O)x(P) f(x) = F(x(P)) – F(x(O)),
in diesem Fall
(2.2) A– = x³(P) – x³(O) = 8 – 0 = 8.
Allerdings ist die obere Begrenzung der Fläche die Normale nP(x).
Deshalb muss noch ein Dreieck hinzugefügt werden, dass von nP(x), der x-Parallelen bei y(P) und der y-Achse gebildet wird. Für die Höhe dieses Dreiecks braucht man neben der Grundseite x(P) noch die Steigung bzw. das Gefälle. Nun ist nP(x) senkrecht zur Tangente tP(x), die ihrerseits die Steigung f'(x(P)) hat, in diesem Fall 6x(P)=12.
Die Steigung von nP(x) ist mithin –1/(f'(x(P)), in diesem Fall also nP'(x)=–1/12. Dies mal der Grundseite ist die Höhe, und so liefert die Dreiecksflächenformel
(3) ΔA = ½·|nP'(x)|·x²(P) = ½·1/12·4 = 1/6
Die ganze Fläche ist also
(4) A = A0 + ΔA – A– = 24 + 1/6 – 8 = 161/6 .
Das Bild, das die Sache veranschaulichen will, ist eine Prinzipzeichnung. Eine maßstabsgerechte Zeichnung würde das Dreieck kaum erkennen lassen.
Normale ausrechnen (Senkrechte zur Tangente bei x=2; Steigung orthogonal) ---- Steigung gewinnt man aus der 1. Ableitung
Differenz zwischen Normale und Parabel bilden.
Von 0 bis 2 integrieren.
Hey, Stichwort lautet Integralrechnung mit welcher man die Fläche zwischen x- Achse und Graph bestimmen kann.
Bei dieser Aufgabe kannst du wie folgt vorgehen:
- Rechne die gesamte, rechteckige Fläche aus, sprich jene mit den Eckpunkten: A(0/0) B(0/12) P(2/12) D(2/0)
- Nun rechne mit der Integralrechnung die Fläche zwischen Graph und x Achse aus.
- Nun rechnen die Gesamtfläche von 1. minus die Fläche von 2. .
Hey
ich habe eigentlich keine Ahnung, aber ich denke der Pythagoras könnte weiterhelfen
Wenn Du hier ein rechtwinkliges Dreieck siehst, lass mich nicht dumm sterben.
Ich bin mir nicht sicher, dass dies schon Differentialgeometrie ist.
Außerdem wirkt die Form auf mich sehr kompakt, ich würde z.B. die Formeln eher absetzen und nummerieren, etwa so:
Tangentengleichung
(1) yt = ft(x) = f'(x0)(x − x0) + f(x0)
Normalengleichung
(2) yn = fn(x) = (−1/f'(x0))·(x − x0) + f(x0)
(x0 ist der x-Wert des Punktes, in dem die Tangente den Funktionsgraphen berührt und die Normale ihn schneidet).
...