Bestimmten Zeitpunkt aus einem Graphen ablesen?
Hi,
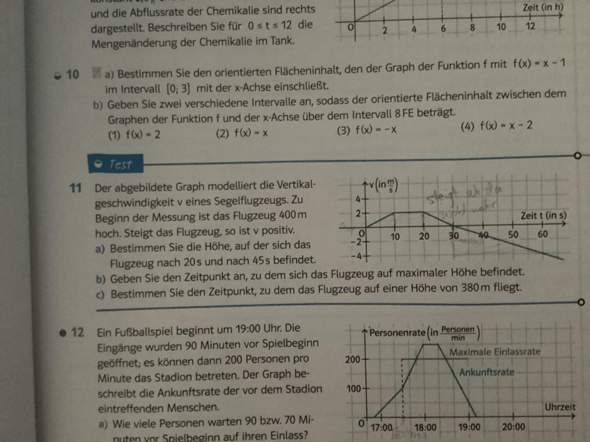
ich verstehe die 11 c nicht, wie soll ich da rausfinden wann es auf 380m fliegt?
in den Lösungen steht bei 60s aber ich verstehe nicht wie man darauf kommt
3 Antworten

Hallo.
Verfolge einfach den Verlauf. In den ersten 10 Sekunden steigt es von 0m auf 2m/s. In der Zeit hat es also an:
10 * 2 / 2 = 10m
Höhe gewonnen. Zwischen 10-20 Sekunden ist der Aufstieg konstant bei 2m, also
10 * 2 = 20m
zwischen 20 und 30 Sekunden nimmt die Steigung wieder ab von 2m/s auf 0m/s
10 * 2 / 2 = 10m
Nach 30 Sekunden, also unmittelbar bevor es anfängt zu fallen, hat es eine Höhe von
400m + 10m + 20m + 10m = 440m
Danach sinkt es konstant in einer Geraden. Wir können zwei Punkte klar ablesen:
(30|0) und (60|-4)
Daraus lässt sich die Steigung der Sinkgeschwindigkeit ableiten:
m = (-4 - 0) / (60-30)
m = -4/30
m = -2/15
Pro Sekunde sinkt das Flugzeug also um 2/15 m/s mehr. Wir suchen nun die Zeitspanne wo Durchschnittsgeschwindigkeit pro Zeitintervall ((2t/15)/2) * Zeitintervall (t) dann die -60m Höhendifferenz (440 - 380 = 60) ausspuckt:
((-2t/15)/2)t = -60
(-1/15)t² = -60
t² = 900
t = 30
Also 30 Sekunden nach dem es angefangen hat zu sinken, ist es auf einer Höhe von 380m angelangt. Es ging nach 30 Sekunden in den Sinkflug über, also nach 30+30=60 Sekunden.
War das verständlich erklärt?

Die Zu- oder Abnahme s der Höhe entspricht dem Flächeninhalt zwischen Funktion und x-Achse. Eine Fläche über der x-Achse bedeutet Zunahme der Höhe, eine Fläche unterhalb der x-Achse entspricht einer Höhenabnahme.
Das resultiert letztlich aus der Formel:
s = v * t
a) s(20), Berechnung der Fläche:
s = 0,5 * 2 m/s * 10 s + 2 m/s * 10 s = 30 m
h = 400 m + s = 400 m + 30 m = 430 m
s(45), Berechnung der weiteren Fläche:
s = 0,5 * 2 m/s * 10 s - 0,5 * 2 m/s * 15 s = 10 m - 15 m = - 5 m
h(45) = 430 m - 5 m = 425 m.
b) Die größte Höhe ist dann erreicht, wenn das Fllugzeug aufhört zu steigen, also bei t = 30 s.
c)
Ansatz: bei 30 s hat das FZ die größte Höhe. Danach sinkt es. Die Fläche des Dreiecks ab 30 s unterhalb der x-Achse muss dabei dem Höhenverlust entsprechen.
Zuerst berechnen wir die Höhe bei t = 30 s:
s(30) = s(20) + 0,5 * 2 m/s * 10 s = 430 m + 10 m = 440 m
Das Flugzeug muss also sinken um:
s(t) = 440 m - 380 m = 60 m
Nun gibt es mehrere Mögllichkeiten, die Aufgabe zu lösen:
a) man denkt gar nicht nach und rechnet nur: führt zur Lösung, dauert aber und ist etwas komplizierter.
b) Man guckt sich den Graphen genau an und merkt: hoppla, das Dreieck zwischen t = 30 s und t = 60 s hat eine Fläche von 0,5 * 4 * 30 = 60 FE. Das ist ja genau der Höhenverlust, den wir suchen und daher:
Lösung: das FZ hat nach 60 s eine Höhe von 380 m.
c) Man denkt nach und rechnet kurz und einfach:
in a) und b haben wir berechnet:
h(30) = 440 m
h(45) = 415 m
Die Dreiecksfläche hat also 15 FE. Wir brauchen aber 60 FE und die erhalten wir, wenn wir v verdoppeln und wenn wir t verdoppeln. Das ist dann genau das Dreieck bei t = 60 s mit v = 4 m/s

Das müsste man eigentlich wahrscheinlich mit einer Formel machen, aber ich bin jtzt nicht in der Materie drinnen deswegen rechne ich es pro 10 sekunden aus:
0s = 400 m
10 s = 1*x+t --> 1*10+400 =410
20 s = 2*x+t --> 2*10+410 (davoriger wert)
30 s = 1*x+t --> 1*10+430 =440
40 s = -2*x+t --> -2*10+440 = 420
50 s = -2*x+t --> -2*10+420 = 400
60 s = -2*x+t --> -2*10+400 = 380
Also beträgt die Höhe bei 60 s 380 m