Geometrie – die neusten Beiträge

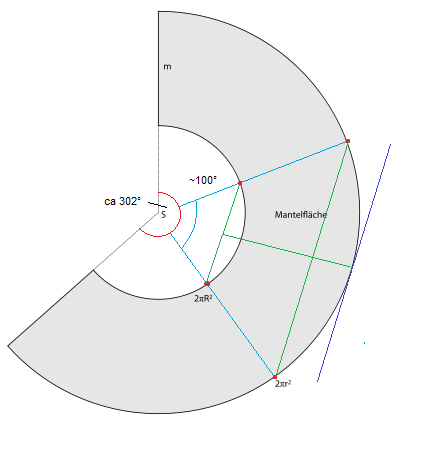
Hey, Wir sollen einen Wassereimer konstruieren in den 10 l rein passen also 10 Kubikdezimeter, der Wassereimer soll ein Kegelstumpf werden (Kegel ohne Spitze) wie rechne ich die Höhe, Radius etc. aus wenn ich nur das Volumen gegeben habe? {Volumen Kegel: 1:3 x Pi x Radius ^2 x Höhe/ Kegelstumpf = gr. Kegel - kl. Kegel} LG

Hey Leute!

Frage steht ja schon oben undzwar geht es um den rot markierten Winkel. Natürlich habe ich es schon selbst versucht, aber viel weiter, als dass α und der entsprechender Scheitelwinkel 80° und dementsprechend die Nebenwinkel 100° sind, bin ich nicht gekommen. Ich weiß, dass es mit dem großen Kreis zusammenhängt, weiß aber nichts damit anzufangen..bei den anderen Aufgaben hatte es ganz gut geklappt nur bei dieser nicht.. Wäre nett, wenn mir jemand helfen könnte :)

Leute ich schreibe bald be arbeit !!!!und ich habe vieles gelesen?!?ich weiss das ein quader ein körper ist aber die selbe eigenschaft wie ein rechteck hat!!!aber was ist ein quadrat???ist ein quadrat das selbe wie ein rechteck(nur als eigentsxhaft )oder der quader????bitte hilft mir

Hallo, könnt ihr mir bitte sagen wie man ein Dreieck mit dem winkel alpha (22 1/2), Beta (80) und eine winkelhalbierende auf gamma (6) konstruiert? Ich komm wirklich bei der aufabe nicht weiter und es wäre sehr hilfreich wenn ihr mir helfen könntet. Danke im voraus!

wer hat den Umkreis eines Dreiecks erfunden

Ist ein Drachenviereck ein rechteck und umgekehrt? LG Ap4rat

Hallo! Ich habe eine Matheaufgaben mit der ich nicht weiter komme: ein Tetraeder hat die Eckpunkte A(-3/3/2), B(7/5/2), C(2/-7/2) und P(1/1/10). Im Punkt P ist ein Pendel befestigt, welches senkrecht nach unten durch die Grundfläche aus den Punkten A, B und C hängt. Berechnen Sie die Gesamtkantenlänge des Tetraeders.

Hallo zusammen

Eine geometrische Frage: Wenn ich ein Viereck zeichnen muss und dazu die Winkel Alpha (62°), Beta (82°), Gamma (119°) und Delta (97°) sowie die Seite a (7cm) kenne, woher weiss ich dann wo alle Eckpunkte liegen??

Zwei Eckpunkte kann ich aufgrund der Seite a ermitteln. Zwei weitere Seiten kann ich aufgrund der Winkelangaben einzeichnen, ausgehend von a. Aber woher weiss ich wo die anderen Eckpunkte auf diesen neuen Seiten liegen, so dass bei beiden der Winkel stimmt??

Danke im Voraus!!

Gruss R.

hallöchen :) also ich schreib in ca 2 Wochen Abi D-:

und rechne da grad ein paar Aufgaben aus der Analytischen Geometrie ... ich hab jetzt ne Ebene in der Normalenform und muss sie in die Parameterform umwandeln.... aber wie? :( ich hab keine Ahnung... ich könnte jetzt natürlich von der Normalenform zur Koordinatenform und dann zur Parameterform, aber geht das nicht auch ohne diesen Zwischenschritt?

danke im Vorraus :)

Wie kann ich die seitenlänge von einem quadrat berechnen wenn der Durchmesser gegeben ist? Danke schonmal

Ich hab das mal in der Schule gemacht aber ich weißt nicht mehr wie es geht.

könnt ihr mir bitte eine Formel mal dann schreiben

danke

Wenn ich zu einer Ebene E1 eine Parallele Ebene E2 mit dem Abstand 1 zu E1 bestimmen möchte geht man ja so vor:

man nimmt den Betrag des Normalenvektor von E1 und dividiert E1 durch diesen Betrag und schon hat man E2.

Meine eine Frage ist nun, wie gehe ich vor, wenn ich einen Abstand von 2 oder 3 erreichen möchte? Und die andere Frage: Da es ja immer 2 parallele Ebenen gibt möchte ich auch die 2. angeben. Wie macht man das? (einfach ein Minus davor schreiben?)

Hallo zusammen! :) Folgendes Problem: Ich möchte einen Mörtelkübel von Innen mit Linoleum auskleiden. (Als Deko) Jetzt bin ich mir aber nicht sicher wie viel Material ich brauche bzw. wie ich es am Besten zuschneide. Ich habe ja einen Kegelstumpf als Form, der soll mit möglichst wenig Verschnitt ausgekleidet werden. Dazu habe ich bisher das hier bei Wikipedia gefunden: http://de.wikipedia.org/wiki/Mantelfl%C3%A4che (bei Kegelstumpf) Bei dieser Zeichnung beträgt mein Innenradius vom Boden des Kübels R = 255mm, Innenradius Oben r = 305mm und Höhe h = 360mm , m = ca.364mm

Jetzt muss ich diesen Kegelstumpf abwickeln und erhalte Winkel von ca. 302°. Das wäre ja schon fast wieder ein voller Kreis, ich bräuchte also fast schon ein quadratisches Stück, bei dem ich dann die beiden Kreise einzeichne und entsprechend ausschneide. Die Frage ist jetzt: Wie kann ich berechnen, in welche sinnvollen Teilstücke ich die Mantelfläche zerlegen kann und vorallem wie groß diese dann sein müssten? Ich dachte jetzt daran das Ganze in 3 Segmente von je ~100° zu unterteilen.

Interessant wäre für mich die Strecke zwischen den vier Eckpunkten der einzelnen Segmente und die Höhe zum Außendurchmesser. Wie berechne ich das am besten? Ich habe mal eine kleine Skizze angefügt. (Bild stammt von Wikipedia) Hoffentlich erkennt man was ich meine.

Hat jemand Tips wie ich das am besten mache? :)

Schöne Grüße

Warum kann man an keinem Geobrett ein gleichseitiges Dreieck spannen? Bitte um leicht verständliche Antwort :)

Hallo Ihr Lieben und zwar wollte ich meinen Sohn bei den Mathe aufgaben helfen leider blicke ich da garnicht durch... Könnt ihr mir da bitte helfen also es wäre nett wenn mir das mal einer erklären könnte wie es aussehen soll.. Und zwar zur aufgabe.. In ein Koordinatensystem soll folgendes gemacht werden A) markiere die punkte P (1/1,5) und Q (4/0,5) und zeichne durch P und Q die Gerade ( das konnte ich ihn helfen)

Den Rest verstehe ich irgendwie nicht wie das gemeint ist??

B) zeichne in den Punkten P und Q jeweils die senkrechte zu PQ.

C) markiere auf jeder senkrechten einen Punkt im Abstand von 1.5 cm zu PQ.

Wenn mir jmd. helfen kann wäre es Nett will und bitte nicht direkt beleidigen oder sonst was...

Danke im Voraus

Wie berechne ich die Länge der Grundkanten bei einem Quader mit quadratischer Grundfläche, wenn ich das Volumen und die Höhe habe? (V=300cm^3 und h=12cm).

Hi. Kann mir bitte jemand sagen wie das verhältnis (x/y) eier konserve sein muss damit man mäglichst wenig bleuch dafür braucht ? x= höhe y= durchmesser. wenn es möglich ist bitte auch den lösungsweg einfügen.

danke im vorraus

Angenommen eine Rampe ist rechteckig und die Länge unterschiedlich lang wie die Breite. Aber die Neigungen in beide Richtungen sind verschieden. Dann komm ich ja komischerweise auf 2 unterschiedliche Höhen. Und wie komm ich dann auf die Steigung der Diagonalen?

Wenn die Seite a= 4 cm ist und die Seite b= 5,2cm, wo muss ich dann mit dem Zirkel einstechen ? Bei Punkt A oder bei Punkt B ? Und auf wieviel cm muss ich den Zirkel dann einstellen ?

Hallo Ihr lieben, ihr könnt mir doch bestimmt weiterhelfen:

Wie berechne ich eine Winkelabweichung: Also angenommen habe ich in der Ecke an der Wand der keinen 90 Grad sondern nur z.B. 89 Grad. Wie berechne Ich nun die Abweichung wenn die Wand 4m lang ist? Dafür gibts es eigentlich eine Formel kann aber absolut nichts finden.

Danke :)

Weswegen Passt Schwarz und Weiß so perfekt zusammen obwohl sie doch komplett gegensätzlich sind?

Wie unterscheide ich die Seiten "A" und "B" ?

Hallo,

muss man zum quadrieren eines Vektors das Kreuzprodukt oder das Skalarprodukt mit sich selbst nehmen? Oder etwas ganz anderes?

Danke

hey leute,

wie man an der fragestellung wohl sieht mach ich grade mathe und verzweifle grade daran :s naja also die Aufgabenstellung ist: Geben Sie eine normalengleichung für eine ebenenschar an, deren ebenen alle zueinander parallel sind. Erläutern Sie, warum Ihre Lösung eine solche Ebenenschar festlegt :S

Also ich hab mir jetzt gedacht, dass doch für eine parallelität gegeben sein muss, dass a1/b1=a2/b2=a3/b3 ist. und die noralengleichung ist ja Vektor n * (Vektor x - Vektor a). Doch wie geh ich jetzt weiter vor :S

lG Charlie

Hi😄 kann mir mal jemand erklären, was ein Wehwinkel ist? Also wie hier auf dem Blatt steht. Muss ich einfach den Punkt finde von dem man zwei Linien zu den jeweiligen Seiten ziehen könnte und dann ein rechter Winkel entsteht?

Wie die Überschrift es schon sagt, woran erkenne ich die Grundseite eines Dreiecks? Falls jemand antwortet bitte so einfach wie möglich erklären:D danke im vorraus.

Hey ich möchte ein Dreieck konstruiren... Gegeben sind:

a=4cm

c=8cm

Winkel Gamma = 110 Grad

Ich weiß ja nicht den Winkel Beta oder Alpha, wie soll man das Dreieck konstruieren?

1. seite c zeichnen
2. was dann? Bitte helft mir ... Ich lerne gerade für ne Arbeit, und würde das gerne verstehen...

Ps: ich hab einen Zirkel und ein Geodreieck;) Lg aus Berlin Theo

Hallo, ich habe eine kleine Meinungsverschiedenheit mit einem Arbeitskollegen . Es geht um die Frage, um eine Ellipse unrund ist (unrund gem. der Definition von Wikipedia: https://de.wikipedia.org/wiki/Unrund. Kann mir das jemand beantworten? :)

Beispiel: a = 5,7 cm; f = 7,9 cm; d = 3,3 cm

Als erstes: wie soll ich ein parallelogramm mit e oder f zeichnen? Das hab ich noch nie verstanden. Dann: ich hab es mal versucht so zu zeichnen: hab mit d=3,3cm angefangen und dann mit'm zirkel (auf 7,9cm eingestellt) auf beide seiten (kp wie das heißt) eingestochen und jeweils ein halb kreis gezeichnet. Dann hab ich einfach von den D punkt bis zur der stelle ein strich(f) gezogen wo sich die kreise schneiden. Und hab dann ein A strich dahin gemacht wo a und f 5,7cm auseinander sind. Jetzt hab ich nur nochmal 3,3cm von a nach oben gezeichnet ( der b strich oder so) und alles verbunden.

Meine frage lautet: war das richtig? Oder gibt es noch einfachere wege? Ich würde ja ein bild rein machen aber mein handy nimmt das irgendwie nicht an und es sieht ja auch eig. Wie ein parallelogramm aus.

.......

Beim Gucken dieses Numberphile-Videos bin ich auf einige Fragen gestoßen, die mit den spärlichen Infos aus dem Video auch nicht beantwortet werden können: https://www.youtube.com/watch?v=Nyo3TjKyu_c

1. Allgemeine Verständnisfrage: Habe ich das richtig verstanden, dass die Größe der Squäre bzw. Kugel irrelevant ist, aber sich im Umkehrschluss die Größe der Pentagons und Hexagons daraus ergeben?
2. Rechnet man das Ganze nur für Sechsecke oder nur für Quadrate aus, stößt man bei der Eulercharakteristik immer auf: #v - #e + #f = 0 = 2. Läuft da irgendwas in der Formel schief oder bedeutet das tatsächlich, dass es keine Anordnung von Sechsecken bzw. Quadraten gibt, die auf eine Sphäre passt?

Ich habe mal gehört, dass die Summe aller Winkel in einem Dreieck nicht 180 Grad ergeben muss. Warum? Widerspricht das nicht der "normalen" Geometrie? Bei welchen Dreiecken ist das der Fall?

Hi Leute, bevor jetzt jemand nörgelt - nein die ganzen Quellen aus dem Internet haben meinem Verständnis leider nicht weitergeholfen! Ich schreibe nämlich bald eine GIS-Klausur und möchte nun wissen was der exakte Unterschied zwischen Topologie und Geometrie ist. So wie ich das verstehe ist Topologie die Lage und Beziehung der Objekte zueinander und Geometrie lediglich die Form.

Nun, wenn ich aber zwei Rechtecke habe, wobei das zweite etwas schmaler und gedreht ist (um sagen wir mal 45°) ist dann die Topologie oder Geometrie unterschiedlich? Ich mein theoretisch ist ja die Form UND die Lage nicht mehr dasselbe...

Grüße!

Erisesnich

Hallo zusammen ich soll ein Dreieck mit der Seite b= 7 cm, der Höhe ha=5cm und der Seitenhalbierenden sb=6cm konstruieren.

Mein Ansatz lautet so (ich gebe zu ich habe ihn abgeschaut) ich konstruiere zuerst die Seite b, ziehe einen Thaleskreis um b, dann ziehe ich einen Kreis um Punkt A mit der Länge ha=5cm, der Schnittpunkt der beiden Kreise ist der Punkt der Höhe auf der Seite c;

und weiter komme ich einfach nicht, kann mir jemand helfen? Ich wäre sehr dankbar

Hallo, ich bin im Moment dabei ein Spiel (2D) zu programmieren. Die Frage betrifft aber eher die Mathematik im Hintergrund. Also ich habe einen Winkel gegeben und möchte ein objekt in diese richtung bewegen. Ich kann objekte aber nur mithilfe von Vektoren, bzw. einer x und y koordinate bewegen. z.B. x=2 und y=3 bewegt es sich eben zwei nach rechts und 3 nach oben. wie kann ich jetzt aus einem winkel (und einer Länge) diese Koordinaten herausfinden?

Nein, ich brauch das für keine Hausaufgabe, da ich sowieso Ferien habe. Aber ich dachte mir grade ich lern mal ein bisschen Mathe und da seh ich eine Aufgabe, die mir unmöglich scheint, da nur die Hypotenuse gegeben ist.

Wenn es euch nichts ausmacht schreibe ich die Textaufgabe.

Die Seiten eines 19-Zoll-Bildschirmes (die Hypotenuse, da Diagonale, 19 Zoll= 48,26cm) stehen zueinander im Verhältnis 5:4. Wie hoch und wie breit ist der Bildschirm in Zentimetern.

Ihr müsst mir die Aufgabe auch nicht unbedingt lösen, ich brauch nur einen Gedankenanstoß, wie ich solche Aufgaben in Zukunft lösen kann (also wenn z.B. nur die Hypotenuse gegeben ist und sonst nur ein Verhältnis)

Danke im Voraus!

Ich frage das ganz allgemein: Ist es sinnvoll, bei Mathe zu versuchen, die Formeln wirklich zu verstehen oder sollte man lieber akzeptieren, wie sie sind und stumpf auswendig lernen wie in der Schule ? Ich finde es nämlich sehr schade, dass Formeln in der Schule nicht wirklich erklärt werden..........

... mit denen man uns (zumindest vor 25 Jahren) in der Grundschule geometrische Formen näher gebracht hat? Weiß das jemand noch?

Hallo, Ich verstehe meine Mathe hausaufgaben gerade überhaupt nicht. Ich hab nur c und h (höhe) gegeben und soll daraus jetzt alle restlichen Seiten, inklusive der Teilstrecken p und q berechnen. Wie geht das?

Wie genau konstruiert man eine Strecke mit der Länge Wurzel aus 12?

Hallo zusammen,

es wäre sehr nett, wenn mir jemand erklären könnte, wie man eine Gerade an einer Gerade spiegelt. Ich weiß, dass man beachten muss, ob die Geraden parallel sind oder ob sie sich schneiden.

Vielleicht gibt es da draußen jemanden, der mir das Vorgehen anhand dieser Beispiele erklären könnte ;)

g: x= (1/2/3) + t(-1/1/1) h: x= (4/10/-1) + s(0/-2/2) (parallel)

g: x= (1/2/3) + t(1/1/1) h: x= (5/9/0) + s(2/2/2) (nicht parallel)

P.S falls jemand auch weiß, wie man eine Ebene an einer Ebene spiegelt, würde ich mich darüber freuen, wenn jemand die Vorgehnsweise erklären könnte und vielleicht noch Ebene/Gerade.

LG

Hallo,

Ich brauche 2 Kubikmeter Kies von 16-32 mm. In einem Big Bag sind soweit ich weiß eine Tonne. Wie viel Kubikmeter Kies sind eine Tonne? Wie viel Big Bags brauche ich?

Vielen Dank im Voraus.

Hallo Leute ich bin rel. neu hier und hab gleich mal ein Problem :/

Ich bin im 2ten Semester und studiere einen technischen Studiengang und komm momentan bei EINEM einzigen Thema nicht weiter was ich aber für meine Hausaufgabe brauch, die muss ich nämlich abgeben weil sie benotet wird -.-'

Es geht um das Epsilon-Delta Kriterium und ich werde einfach nicht daraus schlau ! Bin echt verzweifelt hab best. 5 bücher daheim liegen bei 2 wirds sch***e erklärt und in den anderen wirds garnicht erwähnt :/

Was ist das E.-D.-Krierium und was diese e-d-Kiste? WOZU brauch ich das und wie wendet man sowas an?! hab auch ein bild aus meinem Lehrbuch mal reingestellt ich hoffe so sehr das mir jemand helfen kann....

Vielen Dank schonmal

Hallo, ich möchte gerne in Erfahrung bringen ob es in Mathematik oder Logik ein Zeichen bzw. Symbol für "Gegenteil" oder "Spiegelverkehrt" gibt. Wenn ich zum beispiel eine beliebige geometrische Figur A habe und eine Aussage treffen möchte über ein spiegelverkehrtes Äquivalent... wie mache ich das?

vielen dank vorab, AJ

Hallo,

ich gebe mehreren Schülern Nachhilfe in Mathematik. Doch jetzt hat einer aus der achten Klasse eine Aufgabe bekommen, die ich echt nicht durchblicke. Ich weiß nicht, ob das ein Scherz zum ersten April sein sollte (vielleicht hat er die Aufgabe ja da bekommen), oder ob ich mich einfach nur blöd anstelle.

Die gegebene Geometrische Figur, den Dreipass, hänge ich als Bild an.

In der Aufgabe steht, dass drei Münzen jeweils paarweise aneinander gelegt (so entsteht eben dieser "Dreipass"). Berechnet werden sollen sowohl der Umfang, als auch Flächeninhalt des ZWISCHENRAUMES (kleines krummes Teil in der Mitte der drei Kreise)

Ich habe nach stundenlanger Überlegung immernoch keinen blassen Schimmer. Es wäre daher toll, wenn das gutefrage Team die Frage auch ohne großartigen Rechenansatz drin lässt, notfalls kann ich auch random Formeln für Flächeninhalt & Co hier reinschreiben und nochmal fragen....

Bitte helf mir :S :D

Zeichne einen Kreis und konstruiere 3 Tangenten so, dass deren Schnittpunkte ein gleichseitiges Dreieck bilden. Wer kann mir helfen?? Ich weiß wie man einen Kreis und Tangenten zeichnet und ich weiß was ein gleichseitiges Dreieck ist! ^^ DANKE!!

ich muss zum 1. mal eine GFS halten über den satz des thales und habe keine ahnung wie bitte hilfe

ist die grundfläche und der flächeninhalt das gleiche ,weill in meinem heft rechnet man beides : g . h : 2 .

Ich steh leider total auf der Leitung, habs probiert umzurechnen aber bekomms einfach nicht hin.

Also meine Frage:

Wenn die Sonne in meinem Bild 10 cm groß ist, wie groß sind dann die anderen Planeten und in welchem Abstand stehen diese?

Würd mich echt freuen wenn mir da wer weiterhelfen könnt! :)

Hallo, wollte eben mal fragen, (ich denke es heißt Satz des Thales) wie man ein dreieck durch eine wurzel konstruiert?? Wir haben dies in der Schule (8. Schulstufe) gelernt, doch dies nur 10min schnell schnell, das habe ich nicht verstanden.. habe nämlich am Freitag eine Schularbeit..

Mein Sohn hat in der Realschule ein e Zeichnung bekommen mit zwei Geraden, die sich nicht berühren, wenn man sie aber weiter zeichnen würde, stünden sie im rechten Winkel aufeinander. Zählt dies als "stehen senkrecht zueinander"?

Hallo, ich habe eine Frage zu einer Wahrscheinlichkeitsrechnung. Und zwar gibt es einen Multiple Choice Test mit 4 Fragen und jeweils 3 Antwortmöglichkeiten. Nun ist die Frage zu welcher Wahrscheinlichkeit man alles richtig hat, wenn man planlos rät.

Mein Gedanke, da jede Frage ja zu 1/3 richtig ist, 1/3 x 1/3 x 1/3 x 1/3 = 1/81.

Stimmt das?

Hey Leute Ich habe eine wichtige Frage: ich lerne fürs Abitur aber der Taschenrechner überfordert mich ehrlich gesagt ziemlich... Könnt ihr mir sagen Wie ich herausfinde welchen Winkel Die Y-Achse und eine Gerade einschließen von der ich lediglich die Steigung und den Y-Achsenabschnitt habe? kann mein Taschenrechenr das? oder muss ich zuerst ne Gradengleichung aufstellen? An all die die den taschenrechner nicht haben: schon ein Ansatz wies mathematisch funktionieren könnte würde mir unter Umständen helfen... Aufgrund eines extremen Zeitproblems also AUFFORDERUNG AN ALLE: Schreibt was immer euch dazu einfällt keine Antwort ist zu dumm (außer sie hat nix mit dem Thema zu tun ;) ) Vielen vielen Dank schon mal im Vorraus!!!

ich verstehe irgendwie nicht ganz wie archimedes das 96 eck konstruiert hat. ich kann im internet nichts finden, was mir das begreifen vereinfacht und gut veranschaulicht. am besten wäre natürlich ein video oder eine schritt-für-schritt abfolge, aber ich finde dazu nichts..

soweit ich es verstanden habe, hat er erst im inneren eines kreises ein gleichseitiges sechseck gezeichnet... und dann ? wie kam er auf das 96 eck und wie gelang es ihm ungefähr den flächeninhalt des kreises zu berechnen und dadurch pi herauszufinden, bzw für die damaligen verhältnisse. kam er dadurch auf die 22/7 ?

Das ist eine Aufgabe für eine Freudin, die in der 4! Klasse ist. Wir kommen einfach nicht dahinter. Vlt schafft ihr es ja?

Wenns geht bitte mit Bild!

Herzlichen Dank!

khjk155

,,Wie konstruiert man verschiedene Winkeln?''

Am Monatg & Dienstag habe ich Gymnasuim-Prüfung und brauche einbisschen Hilfe.

Ich habe überall nachgesucht, wie man Winkel konstruiert, aber habe nichts gefunden oder gefunden aber nicht nachgekommen.

Ich weiss wie man 90 Grad, 60 Grad, 45 Grad konstruiert. Aber die anderen Grade weiss ich nicht wie man sie konstruiert. Z.B. 89, 65,27, 72 oder 50 Grad.

Kann jemand es erkären, aber nicht viel zu kompliziert (einfach).

Im Test muss man zeigen wie konstruiert hat und Geodreieck zählt nicht.

Danke im Voraus

Hab grad nen Blackout..Wo ist z.B. bei einem Viereck oder Würfel die Länge, Breite und Höhe?

Wie rechnet man das Volumen von einen Schwimmbad das auf der anderen Seite tiefer ist? ( Bild)

Ich habe ein Problem und zwar müssen wir für die nächste Mathestunde erklären und verstehen können wie der Beweis von Bhaskara geht. Nach sämtlichen recherchen in Google bin ich auch nicht fündig geworden und wurde noch mehr verwirrt. Könnte mir daher jemand den Beweis von Bhaskara kurz erklären :) ? Danke für eure Hilfe .

Hey

Wie benennt man winkel z.B ACB oder BAR Unser Mathelehrer sagt immer entgegen den uhrzeigersinn, aber bei mir kommt immer was falsches raus.

Kann mir das einer erklären?

Danke im Voraus

Hallo erstmal :-) Kaum zu glauben.. aber wahr und auch ein wenig peinlich..... Ich braeuchte Ideen fuer eine Mathe Hausaufgabe der 1. Klasse !! Meine Tochter soll auf ein A4 Blatt Umrisse von runden, quadratischen und dreieckigen Dingen des Haushalts abmalen.. Rund und viereckig kein Problem... Soweit alles easy... Aber was fuer DREIECKIGE Dinge habt ihr zu Hause? Ausser einem Eiskratzer bin ich bisher nicht fuendig geworden und mir faellt auch nichts mehr ein.. euch hoffentlich schon .. Vielen Dank :-)

Brauche Hilfe !!!

Hey, ich hab ne Frage zu einer Drei-Tafel-Projektion:

Die Aufgabe ist, eine Ansicht einer Drei-Tafel-Projektion zu vervollständigen - Ansicht AA und Draufsicht sind gegeben, jedoch ist die draufsicht um 20° gedreht. Meine Frage nun: Kann man die fehlende Ansicht überhaupt mit Hilfslinien erstellen oder muss man die einfach "freihand" zeichnen, da alle nötigen Höhenangaben ja vorhanden sind. Kann sein das ich grad einfach nur aufem Schlauch stehe und die Frage total dumm ist, aber es ist auch schon 22 Uhr :D

Wäre auf jedenfall dankbar wenn mir wer helfen kann. Hab zur veranschaulichung noch das Bild dazu hochgeladen ( Der obere Teil hab ich einfach nur verdeckt, weil da paar Infos für ne weiter Aufgabe stehen, die für diese Aufgabe nicht relevant sind)

wie kann man radius und höhe von zylinder berechnen wenn oberfläche und volumen gegeben sind ?

und wie kann man radius und höhe von zylinder berechnen wenn oberfläche und Mantelfläche gegeben sind ??

Hey, wir haben in Mathe eine Aufgabe bekommen wo wir den Oberflächeninhalt des Thetraeder rausfinden sollen. So ich habe jetzt auch schon überall geschaut und habe auch die Formel für die Höhe a² durch 2 * wurzel 3. Diese Formel habe ich auch soweit verstanden. Allerdings verstehe ich hier schon nicht, warum ich die für die Berechnung des Oberflächeninhaltes brauche. Dann gibt es ja auch noch die Formel für die Fläche a² durch 4 mal Wurzel 3. Dann lautet die Formel für den Oberflächenihalt ja a² mal Wurzel 3. Aber wie kommen sie darauf? Kann mir vielleicht einer helfen?

Was ist ein Fußpunkt? Bin gerade am Lernen weil wir morgen Schulaufgabe schreiben und ich weis nicht was ein Fußpunkt ist.

Hi!

Ich wollte hier grad so ein Modellhaus bauen für den Kunstunterricht und ich hab schräge Wände für mein Haus geplant. Der Winkel beträgt bei meiner Zeichnung 65 Grad und 1cm entspricht 1m. Jetzt wollte ich es bei meinem Modell so machen, dass 2cm 1m entsprechen.

Ändert sich dann auch irgendwie der Winkel bei meinen Wänden?

Ich wäre euch sehr dankbar für eure Antworten!

Warum ???

Warum ist der Schnittpunkt der mittelsenkrechten gleichzeitig der Umkreismittelpunkt? Bitte schnell antworten!

Danke..! :)

Kann mir jemand ein paar Vorteile und Nachteile als Architekt nennen?

Mich interessiert es, ob es möglich ist, eine Strecke von z.b 8 cm nur anhand von Zirkel und Lineal durch 3 zu teilen. Wie?

Hi,

wie kann ich ein gleichschenkliges Dreieck konstruieren, wenn nur eine Höhe sowie eine Winkelgrösse gegeben ist?

Also z. B. hc = 6cm, Gammna = 75° oder hc =7 cm und Beta = 70°?

Wäre über eine Antwort froh. :-)

Hier zur Frage: Gegeben sind die beiden Geraden g: x= Vektor(2;-1;0)+ r* Vektor(3;-1;2) und h:x= Vektor(1;1;-1) + s* Vektor(2;b;c)

Frage) Schneiden sich g und h im Punkt P(-13/4/-10)?

Bitte um Hilfe wäre super nett !

Wozu brauchen wir sie im Alltag / allgemein

Das Thema ist Descartes, aber ich verstehe die Zeichnung und den Text nicht im zusammenhang?!

Hallo ihr Lieben, ich mach gerade meine Hausaufgaben in Mathe und mir ist ein Wort aufgefallen, das unser Lehrer uns schon mal erklärt hat, was ich aber nicht mehr weiß :D...Also, was ist eine Planfigur? Hoffe ihr könnt mir weiterhelfen <3

Ich muss demnächst mit zwei anderen Mitschülern ein Referat über Pi halten (Powerpoint, 9.Klasse). Bevor wir uns treffen soll jeder zwei Themen zu Pi vorbereiten und ich habe unter anderem das Thema Geometrie. Doch wenn man in Google nach "Pi Geometrie" oder "Pi in der Geomtrie" usw. sucht, findet man nichts passendes :( Also was gehört alles zum Thema Geometrie, wenn man ein Referat über Pi halten muss?

Danke

Hey leute wie berechne ich es welche werte x annehmen kann? Z.b. Bei der aufgaben stellung; Ein rechtwinkliges dreieck ABC ahz die Kathetenlänve AB = 6cm und BC = 5cm. Verkürtzt man die kathete [AB] um 1/2 x cm und verlängert man gleichzeitig die kathete [BC] um x cm, so entstehen neuen Dreiecke AnBCn.

Heisst es dann das x<12 sein? Weil sonst AB 0 hat oder welche belegung ist sinnvo?

Wie kann ich punkt und Achsensymmetrie unterscheiden?

Was sind die Vor- und nachteile eines Zweitafelbildes. Finde bei Google leider nicht darüber.

Freu mich auf Antworten Lg Cocomilk

Hallo Leute

Ist es möglich einen Kegelstumpf nur mit dem Winkel der Höhe und des Radius r1 zu berechnen? Winkel: 25Grad Höhe : 4mm r1: 2mm (kleine Fläche)

Grundfläche =?

Der Grund für meine frage ist folgender. Ich benutze konische Fräsen die an der spitze 1-3mm breit sind und einen Winkel von 20 o.25 o.30 grad haben. Wenn ich mit dem Gräser 1mm tief fräse, müsste ich wissen wie breit der Kanal an der Oberfläche ist.

Könnt ihr mir helfen. Vielen Dank Lg

Hallo ich habe die aufgabe einen Farbkreis nach Johannes Itten's 12 Teiligen Farbkreis zu konstruieren und ich weiß echt nich wie ichs hinbekomme das am ende alle 24 felder gleich groß sind (währe ja schon ein erfolg überhaupt mal 24 felder hinzubekommen) habt ihr irgentwelche hilfreichen techniken ?

Hallo Ich kann die folgende Geometrieaufgabe nicht lösen: Auf einem Billiardtisch habe ich zwei kugeln. Wie muss ich Kugel A anstossen damit sie über drei Banden die Kugel B berührt und wie soll ich das konstruieren?

Hallo zusammen,

ich habe eine Frage an euch :) weis jemand was das Gegenteil von geometrischen Formen ist? Also in gewisser Weise das Gegenteil von Malewitschs schwarzen Quadrat in purer Form... Was wäre das gedankliche Gegenstück? Bin für jeden Hinweis dankbar :)

viele grüße ana

Hi, wenn ich als Flächenmaß 100m² habe, ist es doch egal was für eine Form diese Fläche hat. Da die Fläche immer 100m² hat, muss der Umfang auch immer gleich sein. Davon gehe ich aus. Wieso gibt es keine universelle Formel um den Umfang einer Fläche zu berechnen? Alle wollen Angaben ob es ein Quadrat oder Rechteck ist und eine Seitenlänge.

Gibt es keine Formel die nur mit der Flächenangabe den Umfang berechnet?

Grüße

warum werden Muskeln größer wenn man sie anspannt. Sie werden ja härter und da dachte ich sie ziehen sich zusammen aber dies ist ja nicht der Fall? :o

So nen komischer Typ behauptet ein kreis hätte unendlich Ecken. Stimmt das? Hat ein Kreis wirklich ecken???

Mann sieht sehr oft, dass bei Brücken Bögen und Dreiecke verwendet werden, aber warum werden diese Formen gewählt bzw. Was macht diese Formen besonders stabil??

Hi. Also in der Aufgabe steht: Ein Prisma hat als Grundfläche ein Dreieck mit a-15cm b-13cm und c-4cm und der Höhe HC-12cm. die Höhe des Prismas ist h-8cm. berechne Volumen und Oberfläche.

Also. Was ist HC? BITTE SUPPORT; NICHT LÖSCHEN!!! danke an alle hilfreichen antworten!

Hallo,

ich muss folgenden Körper in allen sechs Ansichten zeichnen. Im Prinzip ist das ganze kein Problem, nur muss ich die Bemaßung an hand der Skizze selbst ermitteln. Wie gehe ich denn da vor? Mich irritieren die Schrägen etwas...

Schon mal Danke für eure Antworten

Hallo, ich habe hier mal eine Frage zur Geometrie :O und zwar wollte ich wissen, was der Unterschied zwischen Winkel ABC und Winkel CBA ist. Oder ist das dass gleiche?

LG aka901

Hey, ich hätt da mal eine frage, ich verstehe etwas bei den Normalvektoren nicht, es gibt ja Normalvektoren nach links und nach rechts von einem Punkt bzw vektor und wenn dann steht "Was ist der Normalvektor von (3/4)" ist es dann (-3/4) oder (3/-4)

Bitte um Hilfe

Haey Leute..

Ich muss morgen in Mathe ein Referat über Ähnliche Figuren halten. Ich weiß was das ist und wie man die macht und so, aber ich möchte noch ein paar Beispiele nennen wo Ähnliche Figuren im Alltag vorkommen. zB Auf einer Karte wegen dem Maßstab und so.

Vielen Dank schonmal =)

`Träume nicht dein Leben, sondern lebe deinen Traum´

Hallo wir haben heute von unserem Mathe Lehrer eine Aufgabe bekommen die lautet: Konstruiere einen Winkel der Größe:

a) 30 Grad

b) 45 Grad

c) 75 Grad

und das ohne Geodreieck.. wie kriege ich das hin. P.S: Bin in der 7.Klasse

Hallo

Hier habe ich ein paar Fragen zur Geometrie:

1. Was ist die Abbildungen die ein Drehung und eine Spiegelung zurück auf das Ursprungsdreieck zurückführt wie wird es konstruiert?

2. Kann man bei der Tangens-, Sinus-, Cosinus Funktionen usw. die die Seite die zur jeweiligen Winkel gehört als Gegenkathete nehmen z. B

Tangens Alpha(Winkel ab Punkt A)-> Seite a = Gegenkathete.

1. Wie kommt man auf die Resultate für tangens, cosinus und sinus Alpha bei 0 und 90° bzw. wie kann man die beweisen?

Danke

Hallo Leute,

Z.B ein Rechteck ist ja kein Quadrat, warum gibt man die Fläche trotzdem in Quadrat.....(meter, Zentimeter) , an ? Das interessiert mich :D

Danke

Hallo, gibts es Figuren die keine Prismas sind?

Wenn ja wieso sind sie keine Prismen? DANKE!

Hallo!

Also, wir haben in unserem Mathebuch eine Hausaufgabe aufbekommen. Ich habe die ersten drei Aufgaben geschafft, aber an den restlichen dreien bleibe ich hängen. Ich weiß ja nicht mal, ob ich die ersten drei wirklich richtig gemacht habe? Dann habe ich im Internet nach einer Erklärung gesucht, wie so was gemacht wird, habe selber natürlich auch nachgedacht, aber da kommen nur so Grundlernereien, aber ich bin halt im Erweiterungskurs der Sekundarstufe |, da wird es halt mal schon etwas schwieriger. Ich möchte nicht, dass jemand mir das vorsagt, sondern es mir nur erklärt, wenn möglich mit Links zu hilfreichen Texten, Videos, Bildern oder dies selbst eingefügt/geschrieben. Denn ich sitze nun schon fast eine Stunde dran und habe auch andere Hausaufgaben auf. Ich wäre euch wirklich dankbar!!!!

moin leuzz, hab aktuell ein kleines mathe- problem, bzw. eine gedächtnislücke: gegeben sind alle drei seiten eines nicht- rechtwinkligen dreiecks. wie kann ich jetzt (mathematisch, nicht geometrisch) die drei winkel berechnen???

danke schonmal :D