Wie verändert sich die Funktionsgleichung einer Funktion, wenn man den Graphen dieser Funktion im Koordinatensystem um einen bestimmten Winkel kippt / stürzt ?

Question

Meine Frage soll genauer lauten -->

Wie verändert sich die Funktionsgleichung einer Funktion, wenn man den kompletten Graphen dieser Funktion im kartesischen Koordinatensystem um einen bestimmten, frei wählbaren Winkel, nennen wir den Winkel mal phi, im Uhrzeigersinn kippt / stürzt ?

Wie verändert sich die Funktionsgleichung einer Funktion, wenn man den kompletten Graphen dieser Funktion im kartesischen Koordinatensystem um einen bestimmten Winkel im Uhrzeigersinn kippt / stürzt ?

Nehmen wir mal die einfache Funktion y = f(x) = x ^ 2

Diese Funktion bzw. der Graph der Funktion soll nun im kartesischen Koordinatensystem komplett um dem Winkel phi = 17,5 ° im Uhrzeigersinn gekippt /gestürzt werden.

Wie lautet die neue Funktionsgleichung y = g(x) der zu kippenden Funktion y = f(x), die um einen Winkel phi im kartesischen Koordinatensystem im Uhrzeigersinn gekippt wird ?

Es soll nicht das Koordinatensystem selber gekippt werden, sondern die Funktion bzw. der Graph der Funktion im kartesischen Koordinatensystem soll gekippt werden.

Insbesondere interessiere ich mich auch für für den Fall, wie die Funktionsgleichung y = g(x) lautet, wenn man y = f(x) um 90 ° im Uhrzeigersinn kippt, der Graph wäre dann komplett auf die rechte Seite „gestürzt“, die Umkehrfunktion möchte ich dabei vermeiden wenn es geht.

Aber ich interessiere mich für den allgemeinen Fall, mit einem beliebig / frei wählbaren Kippwinkel im Uhrzeigersinn.

Wie verändert sich die Funktionsgleichung einer beliebigen Funktion y = f(x) wenn man sie kippt, wie oben beschrieben ?

Ich interessiere mich also für die veränderte Funktionsgleichung y = g(x)

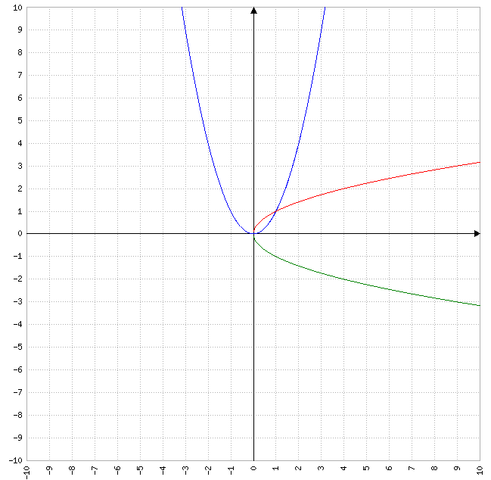
Mir fielen keine besseren Worte als kippen und stürzen ein, hier mal ein Bild von einer Funktion die um 90 ° im Uhrzeigersinn gekippt wurde, damit man sieht was ich überhaupt meine, ich interessiere mich aber für einen allgemeinen Kippwinkel im Uhrzeigersinn, also nicht bloß um die 90 °, aber insbesondere um die 90 ° -->

PhotonX · Accepted Answer

Es soll nicht das Koordinatensystem selber gekippt werden, sondern die Funktion bzw. der Graph der Funktion im kartesischen Koordinatensystem soll gekippt werden.

Das ist doch genau das Gleiche, wo siehst du einen Unterschied?

Also:

x -> cos(a)x+sin(a)yy -> -sin(a)x+cos(a)y

Zum Beispiel:

y=x². -> -sin(a)x+cos(a)y = (cos(a)x + sin(a)y)²

Das ist eine implizite Funktion, die man noch nach y lösen müsste (ergibt zwei Lösungen wegen dem y²-Term, was aber auch zu erwarten ist, weil die gekippte Parabel keine Funktion mehr ist!).

hypergerd · Answer

Auch wenn die Hilfreichste Antwort schon vergeben ist, hier mal die genauen Formeln und Bilder:
http://www.gerdlamprecht.de/Liniendiagramm_Scientific_plotter.htm
Beispiel 113 (Parameterdarstellung) einfach den Offset 0.75 entfernen und Abbruch bei iFarb>0
Der Winkel &auml;ndert sich nach jeder Kurve zu: aB[0]+=17.5*PI/180;
Bild 1
Umstellung nach y(x) ergibt in einfachen Liniendiagramm-Koordinaten:
cos(7*PI/72)*pow(1/sin(7*PI/72)*sqrt(4*x*sin(7*PI/72)+pow(cos(7*PI/72),2))-cot(7*PI/72),2)/4-sin(7*PI/72)*(1/sin(7*PI/72)*sqrt(4*x*sin(7*PI/72)+pow(cos(7*PI/72),2))-cot(7*PI/72))/2
Bild 2
F&uuml;r x kleiner -0.73 geht der Anstieg gegen unendlich (Polstelle) und kippt dann wieder runter, was h&ouml;chstens mit einer 2. Funktion gezeichnet werden kann.
(was ich heute mal weg lasse)

Suboptimierer · Answer

Ich habe da etwas mit einer Rotationsmatrix in Erinnerung.

Spiel damit etwas herum. WolframAlpha: {{cos 17.5, -sin 17.5},{sin 17.5, cos 17.5}}multiply{x,x^2}

Das sieht etwas seltsam aus. Ich bin mir nicht sicher, ob ich die Matrix korrekt angewandt habe.

https://de.wikipedia.org/wiki/Drehmatrix

Wie verändert sich die Funktionsgleichung einer Funktion, wenn man den Graphen dieser Funktion im Koordinatensystem um einen bestimmten Winkel kippt / stürzt ?

3 Antworten