Funktionsgleichung Graphen zuordnen?
Woran kann ich erkennen welche Funktion zu welchem Graphen gehört ?
4 Antworten
Zunächst hast du das "globale Bild":
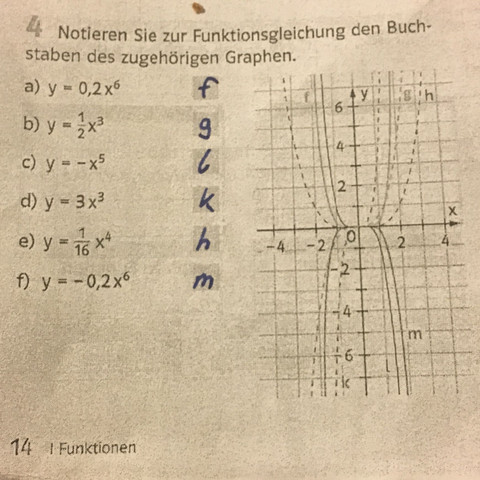
Positives Vorzeichen, geradzahlige Potenzen, wie zb x² kommen "von links" von +unendlich, werden dann kleiner und gehen "nach rechts" wieder ins positive - du hast daher eine "u-Form"
Negatives Vorzeichen, geradzahlige Potenzen, wie zB -x² sieht im Prinzip aus wie die obige Funktion, nur ist sie um die x-Achse gespiegelt. Du hast also eine "n-Form" (ein umgekehrtes U)
Positives Vorzeichen, ungeradzahlige Potenzen, wie x³ kommen "von links" aus dem Positiven und wandern "nach rechts" ins Negative.
Negatives Vorzeichen, ungeradzahlige Potenzen, wie -x³ kommen "von links" aus dem Negativen und wandern "nach rechts" ins Positive. (ist also wieder das um die x-Achse gespiegelte Bild der vorangegangenen Funktion)
Um genauere Unterscheidungen zu treffen, kannst du nun Werte für x einsetzen und den Funktionswert ausrechnen. Suche dir dazu Punkte, an denen sich die Kurven unterscheiden und die "möglichst schön" auszurechnen sind.
Und tu mir und dir bitte einen Gefallen:
Lerne das, was ich hier geschreiben habe nicht auswendig, sondern überlege dir, warum das so ist! Die beste Übung dazu wäre, bei jeder Funktion 3 oder 4 Werte (jeweils beide Vorzeichen) einzusetzen. und zu schauen, wie die Funktion verläuft!
Wenn du gar keine Idee hast, würde ich mir Gitterschnittpunkte aussuchen durch die eine Funktion läuft. Zum Beispiel liegt (2|1) auf h.
Dann setzt du nach und nach 2 in die Funktionsgleichungen ein und wenn 1 heraus kommt, hast du dein h gefunden.
h brauchst du dann natürlich für die nächste Funktion nicht mehr testen.
je höher der Quotient, desto steiler steigt die Kurve, wenn die Steigung negativ ist, sind alle Werte unter 0
in x zahl einsetzen
ausrechnen
und vergleichen wo der punkt auf y ist
Es handelt sich hierbei nicht um Geraden, der Faktor vor dem x ist nicht die Steigung!
Die Steigung von zB 0,2 x^6 ist für negative x negativ, dannoch sind hier alle Werte >= 0.