welche gebrochene, rationale Funktion gehört zu welchem Graf?

Welche Funktion gehört zu welchem Graph ich verstehe das nicht und weiß nicht wie ich das zuordnen muss
6 Antworten
Mit etwas Übung kann man bei gebrochen-rationalen Funktionen direkt das Unendlichkeitsverhalten ablesen - sind z. B. wie hier Zähler- und Nennergrad gleich, dann bilden die Koeffizienten der jeweils höchsten Potenz die waagerechte Asymptote, also bei f ist die 2/3 und bei h 1/1=1. In beiden Fällen kannst Du damit aus den gegebenen Graphen sofort die richtigen ermitteln!
Ein weiteres oft eindeutiges Kriterium sind die Definitionslücken (sind dort, wo der Nenner Null wird). Setzt man den Nenner von f Null und formt um (kann man mit etwas Übung auch im Kopf), kommt man auf x=+/- 2/Wurzel(3), also 2 Def.-Lücken, was hier auch sofort zum Ziel führt, ohne 2/W(3) überhaupt ausrechnen zu müssen.
Mit "etwas mehr Übung" sieht man bei f auch, dass dies eine gerade Funktion ist (Zähler und Nenner sind jeweils gerade), d. h. der zugehörige Graph muss achsensymmetrisch zur y-Achse sein, und das ist hier auch nur einer der 6 Graphen...
Helfen diese Eigenschaften mal nicht sofort weiter, gibt es noch die Nullstellen (sind dort, wo der Zähler Null wird). Dies würde hier zumindest bei h eindeutig zum Ziel führen.
Als letztes Mittel (hier nicht nötig und auch schwierig) würde man sich konkrete, gut ablesbare Punkte suchen und diese mit den fraglichen Funktionsgleichungen abgleichen, oder umgekehrt einen Punkt aus der Funktionsgleichung berechnen und schauen, bei welchen Graphen dieser passen könnte (letztere Variante vor allem, wenn mal kein Punkt wirklich gut ablesbar ist...).
z.B.:
h(x) hat eine Nullstelle bei x = 1, das trifft auf f(x) und k(x) nicht zu, damit kommt nur Graph (2) in Frage.
f(0) = 5/4
f(1) = -3/-1 = 3
Das kann nur Graph (5) sein
h(0) = -0,5
h(1) = 0
Das kann nur Graph (2) sein.
k(0) = -4
k(1) = Polstelle
Das kann Graph (6) sein.
Schau Dir die Nullstellen der Nenner und die Polstellen der Graphen an.
Dann schaust Du auf das Verhalten im (negativen und positiven) Unendlichen. Asymptoten sind ja eingezeichnet. Und Du schaust, ob die Funktion in der Nähe der Polstelle ins positive oder negative Unendliche geht.
bei -2 muss ein Pol sein

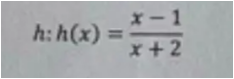
Habe ich ich komme trotzdem nicht weiter