Wieso erhalte ich bei sin,cos und tan unterschiedliche Werte?
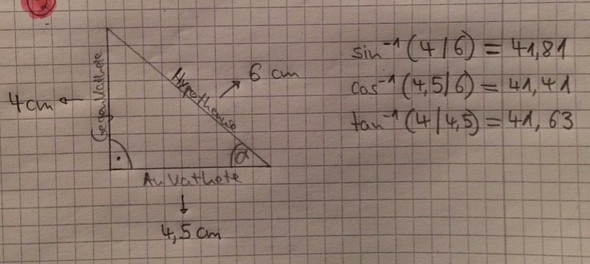
Also, ich habe in beiden Bildern unten ein Dreieck mit rechtem Winkel eingezeichnet. Dann habe ich jeweils alle drei Seiten mit dem Geodreieck gemessen. Nun möchte ich den Winkel Alpha berechnen.
Wenn alle Seiten bekannt sind, müsste ich doch eigentlich mit jeder der drei Winkelfunktionen Alpha berechnen können. Und vor allem müsste ich jeweils das gleiche Ergebnis erhalten.
Bei dem rechten Bild hat das auch geklappt. Ich habe sowohl mit sin als auch mit cos und tan einen Winkel Alpha von 53,13 ermittelt. Doch bei der Zeichnung links und auch bei anderen Beispielen, die ich hier nicht aufgeführt habe, bekomme ich für alle drei Winkelfunktionen unterschiedliche Werte heraus (wie man im Bild links sehen kann).
Meine Fragen: 1) Kann ich wirklich alle Winkelfunktionen gleichermaßen benutzen, wenn alle drei Seiten des Dreiecks bekannt sind?
2) Wieso erhalte ich teils unterschiedliche Werte für den Alpha-Winkel, je nachdem ob ich sin, cos oder tan benutze? Ist das vielleicht auf Messungenauigkeiten zurückzuführen?

8 Antworten
das liegt daran, dass die Hypothenuse nicht genau 6 cm lang ist sondern Wurzel aus 36,25 (also rund 6,02)
Daher die kleinen Abweichungen
die Antwort kommt jetzt zwar etwas spät, aber die Diagonale kannst du ja immer mit dem Satz des Pythagoras ausrechnen.
Die anderen Seiten kann man ja genau bestimmen, wenn die genau in die Kästchen passen
Das liegt daran, dass 4.5^2 + 6^2 genau 7.5^2 ist, 4^2 + 4.5^2 aber nicht genau 6^2.
Wenn dir eine Seite fehlt, dienen ja genau die Winkelfunktionen dazu, sie exakt auszurechnen. Wenn zwei Seiten gegeben sind, kann man es auch immer mit dem Pythagoras kontrolllieren, ob es sich um ein rechtwinkliges Dreieck handelt.
Gezeichnet wird ab jetzt nur noch im Notfall.
Man kann alles rechnen, und zwar genau!
(Oder sagen wir mal: genauer als beim Zeichnen. Manchmal muss man ja kriminell runden.)
1) Ja, grundsätzlich kann man das, natürlich.
2) Dein Fehler ist, die schräg zu den Kästchen liegende Seite auf eine ganze Zahl Zentimeter-Millimeter zu runden, das geht aber nicht, tatsächlich besitzt sie einen Wert, den du niemals mit einem Lineal messen könntest. Daher die Abweichungen. Zum richtigen Ergebnis kommst du, wenn du mit den Seiten rechnest, die auf den Kästchenlinien liegen.
Danke für die Antwort! Was mache ich nun aber, wenn das Dreieck nicht auf Kästchenpapier ist und die Länge keiner Seite bekannt ist? Dann kann ich doch eigentlich nur messen und mich mit einem ungenauen Ergebnis abfinden, oder?
Wenn keine Seite bekannt ist, musst du natürlich messen. Oft werden Aufgabenstellungen aber so vorgegeben, dass die meisten Werte relativ gerade sind, du könntest dann davon ausgehen, dass doch zumindest zwei Seiten gerade Werte haben sollten - ebendie Seiten, die den rechten Winkel einschließen. Die Hypotenuse hat zwangsläufig (in den meisten Fällen) einen ungeraden Wert, das ist anders gar nicht möglich.
Der Fehler kommt durch die Messungenauigkeit in Deinem Dreieck. Im linken Beispiel ist die Hypotenuse nämlich nicht 6 sondern 6.02079... cm lang. Das kannst Du Dir leicht mittels Pythagoras ausrechnen. Der korrekte Winkel ist also der mittels Tangens berechnete.
Danke für die Antwort! Was mache ich nun aber, wenn das Dreieck nicht auf Kästchenpapier ist und die Länge keiner Seite bekannt ist? Dann kann ich doch eigentlich nur messen und mich mit einem ungenauen Ergebnis abfinden, oder?
nein, sondern so, wie ich es oben gezeigt habe: Zwei Seiten messen und die dritte berechnen. Dann stimmt auch alles Weitere
Aber trotzdem werden die Werte ja ungenau sein, weil ich mit dem Lineal niemals eine exakte Länge der Seiten bestimmen werden.
Und außerdem werden teils sehr unterschiedliche Werte herauskommen, je nachdem welche zwei Seiten man nimmt.
aber Du stellt damit zumindest die mathematische Grundlage her, nämlich ein rechtwinkeliges Dreieck. Mit Ungenauigkeiten beim Messen muss man leben. Mathematisch behandelt man die, indem man die Messungenauigkeit abschätzt und Toleranzen angibt.
Danke für die Antwort! Was mache ich nun aber, wenn vom Dreieck keine Seitenlänge bekannt ist? Dann kann ich doch eigentlich nur messen und mich mit einem ungenauen Ergebnis abfinden, oder?