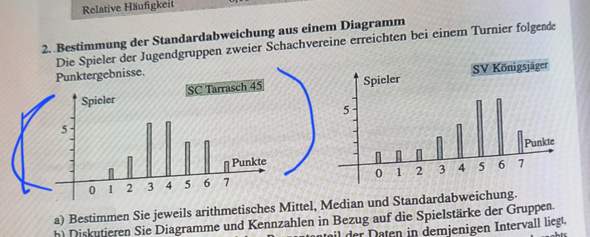
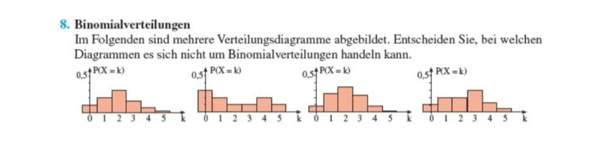
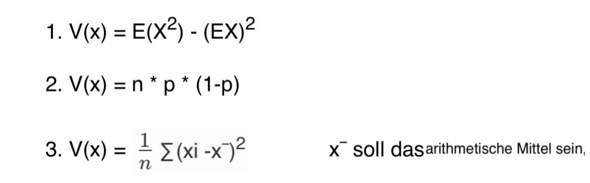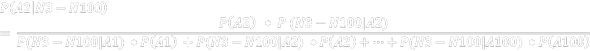Angenommen: Wir haben 100 Türe, hinter einer Tür ist ein Auto, hinter dem Rest Ziegen.
Gast wählt Tür 1, Auto ist hinter Tür 2, Moderator öffnet Türen 3 bis 100.
Ansatz:
Satz von Bayers:
Wir wollen also die Wahrscheinlichkeit berechnen, dass das Auto hinter Tür 2 ist (A2), wenn die Türen 3 bis 100 geöffnet wurden (N3-N100)
Für P(N3-N100|A2) habe ich = 1
Da die Wahrscheinlichkeit, dass die Türen 3 bis 100 geöffnet werden, wenn das Auto hinter Tür 2 ist und der Gast Tür 1 gewählt hat gleich 100% ist.
Für P(N3-N100|A1) habe ich = 98/99, da man nun auch Tür 2 öffnen kann.
Für P(A1) = P(A2) = .. = P(A100) habe ich 1/100
Da die Wahrscheinlichkeit, dass hinter jeder Tür das Auto ist gleich 1/100 ist.
P(N3-N100|A3) = P(N3-N100|A4) = .. = P(N3-N100|A100) habe ich gleich 0, da die Wahrscheinlichkeit, dass die Türen 3 bis 100 geöffnet werden, wenn das Auto hinter den Türen 3 bis 100 ist, gleich null ist.
Wenn ich aber nun alles in die obere Formel eingebe bekomme ich 0,01 = 1%, die Wahrscheinlichkeit, dass das Auto hinter Tür 2 sein sollte, sollte aber 99% sein. Wo liegt mein Fehler?