Hallo!

Wie viele Möglichkeiten gibt es, zwei schwarze und einen weißen Turm auf einem 8×8 Schachfeld zu platzieren, sodass kein Turm einen anderen schlägt? (Nur Türme verschiedener Farben können sich schlagen)

LG

Thema Kombinatorik:

Die Anzeige eines Glücksspielautomaten besteht aus neun Leuchtfeldern, die mit den Ziffern 1 bis 9 beschriftet sind.

Nach Einwerfen des Spieleinsatzes leuchten zufällig genau vier Felder auf.

Alle Kombinationen sind gleich wahrscheinlich. Die leuchtenden Ziffern ergeben von links nach rechts gelesen eine vierstellige Zahl.Der Automat wirft am Ende eines jeden Spiels so viele Euro aus, wie die Endziffer der leuchtenden Zahl angibt.Wie viele Euro muss der Spieleinsatz betragen, damit das Spiel fair ist?

Ich weiß, dass der Gewinn mindestens 4€ - Einsatz beträgt, und dass der Erwartungswert 0 sein muss. Ich weiß aber nicht, wie wahrscheinlich die einzelnen Ereignisse sind, da die Zahlen nicht nebeneinander aufleuchten müssen.

Aus den Ziffern 1 bis 9 sollen dreistellige Zahlen gebildet werden. Wie

viele Möglichkeiten gibt es, wenn jede Ziffer nur einmal verwendet werden

darf?

Mein Ergebnis ist 504. Auch ChatGPT 3.5 und 4.0 sagt 504.

Die Lösung meiner Dozentin sagt aber 243. Sie sagt auch ,,Mit zurücklegen", aber da steht, dass die Ziffern nur einmal verwendet werden dürfen, also werden sie nicht zurückgelegt.

wenn man zum Beispiel eine bin Verteilung hat die die Wahrscheinlichkeit für die Anzanl von richtigen Antworten angibt, also laut unserer Lösung muss man wenn man wissen will wie hoch die Wahrscheinlichkeit ist, dass der Schüler 5 und mehr antworten richtig hat die Wahrscheinlihckeiten mit dieser formel von bernoulli oder so ausrechnen, aber das ist doch doppelt gemoppelt, wenn ich 5 antworten richtig habe, dann ist das ja in 6 antworten schon drinne, und die 6 ist in der 7 drinne

also wieso summiert man das trotzdem

Bei bild eins ist der mittelpunkt weiter oben aber beide bilder sind isometrische würfel das heißt von gleicher länge heißt das dann da wo der mittelpunkt weiter oben ist wurde der würfel einfach von weiter oben abgebildet?

Aber wie?



Warum ist es hier 8 über 5? Es ist ohne Reihenfolge ohne Zurücklegen, deswegen die Formel aber woher kommt denn die 8?

Die Nummer b ist es:

Die Aufgabe lautet: Wie viele Möglichkeiten gibt es, aus sämtlichen Buchstaben des Wortes ZARATHUSTRA Wörter zu bilden, bei denen weder A an erster Stelle noch Z an letzter Stelle stehen soll?

Mein Ansatz war: Alle, also 1.663.200, minus Anzahl Möglichkeiten mit AZ feste Plätze.

Ich komme immer auf die Lösung: 1.663.200-136.080= 1.527.120 aber im Lösungsheft steht: 1.103.760

Bitte helft mir mit Erklärungen. Vielen Dank schonmal vorab :)

Hallo, ich habe eine Frage zu Kombinatorik (liegt mir überhaupt nicht).

Im printing geht es generell darum wie löse ich Probleme die so formuliert sind:

was ist die Anzahl von Elementen aus X sodass […].

Konkret wäre sowas:



Meine Überlegung wäre so:

n aus k wobei mit wiederholen und Ordnung unwichtig.

also so:



Vielen Dank 🤩

wenn Zahlen von 1-1000 vorkommen

Folgendes ist gegeben:

{a, b, c, d} ∈ N (die einzelnen Parameter sollen natürliche Zahlen, inklusive 0 sein)

Es muss folgendes gültig sein:

1. 5a + 4b + 3c + 2d = 110
2. a + b + c + d = 30

Die Frage: Wie viele Kombinationen aus verschiedenen Werten für die Parameter sind möglich?

(7, 11, 7, 5) wäre eine mögliche Kombination

(7, 8, 13, 2) z. B. eine andere

Ansätze wären ebenfalls interessant zu erfahren. Lösungen kann man auch gemeinsam finden.

Zusatzfrage: Was ist der durchschnittliche Wert der einzelnen Parameter a, b, c und d?

Alternative Voraussetzungen bei gleicher Fragestellung:

1. 5a + 4b + 3c + 2d = 77
2. a + b + c + d = 20

ODER

1. 5a + 4b + 3c + 2d = 33
2. a + b + c + d = 10

Unwichtig zur Beantwortung der Frage:

Die Aufgabe habe ich mir selbst "überlegt" und sie ist wohl bisher ungelöst.

Die "Inspiration" war das Prinzip der theoretischen Führerscheinprüfung in Deutschland:

Man muss 20 Grundwissens Fragen (aus einem sehr großen Fragenpool) beantworten, von denen jede 5, 4, 3 oder 2 Punkte Wert ist. In Summe müssen die 20 Fragen 77 Punkte ergeben.

Für den Führerschein Klasse B gibt es 10 Zusatzfragen, welche in Summe 33 Punkte ergeben müssen.

Zum Bestehen braucht man mind. 100/110 Punkten und darf nur eine 5-Punkte falsch beantwortet haben.

Insgesamt gibt es ca 1200 Fragen, aber keine Statistiken darüber welcher Anteil von Fragen welche Punktzahl wert ist.

Nur weil es in meiner Theorie-Lern-App einen Modus mit nur, bzw. allen 5-Punkte Fragen gibt, weiß ich, dass es davon insgesamt 139 gibt. Das ist ein Anteil von knapp 12%. (Stand: 08.02.24)

Hallo, kann mir jemand sagen, ob mein Resultat richtig ist? Ich habe leider keine Lösungen dazu, daher kann ich es nirgends nachschauen...

danke im Vorraus

Aufgabenstellung: In einer Schachtel befinden sich 2 grüne Kugeln sowie je 1 schwarze, 1 rote und 1 blaue Kugel.

Nun zieht man 3 Kugeln aus der Schachtel, ohne dass eine gezogene Kugel wieder zurückgelegt wird. Berechnen Sie die Wahrscheinlichkeit, dass mindestens 1 grüne Kugel dabei ist

Mein Resultat ist 0.1, im angehängten Bild sieht man den Lösungsweg.

Guten Tag, ich schreibe eine Mathe-Facharbeit über die wahrscheinlichkeiten im lotto und ich habe die möglichen kombinationen auf 6 richtige im lotto zu tippen berechnet, welche bei 13 millionen nochwas liegt, aber auf vielen (nicht allen) Seiten im Internet steht, dass die wahrscheinlichkeit bei 15 millionen nochwas liegt. Aber eigentlich ist die wahrscheinlichkeit ja alle möglichen kombination, oder nicht?

Kann mir jemand bei dieser Aufgabe helfen?

Wieso diese mal 14 und nicht mal 15.

es sind doch 15 tulpen

Kann mir bitte jemand bei dieser Aufgabe helfen verstehe die nicht

Ein Basketballspieler hat bei Freiwürfen die Treffer-Wahrscheinlichkeit p=0,5. Er führt fünf Freiwürfe aus.Wir nehmen an, dass sich seine Trefferwahrscheinlichkeit nicht ändert, und dass die Ergebnisse der fünf Würfe unabhängig voneinander sind. Stelle die Wahrscheinlichkeitsverteilung der Zufallsgröße „X=Anzahl der Treffer bei fünf Würfen" auf.

Tipps:

• Zeichne ein "angedeutetes" (also unvollständiges) Baumdiagramm.
• Verwende die Abkürzungen T für "Treffer" und N für "Nicht-Treffer" ("Niete").

Habe bis jetzt ein baumdiagramm mit 3 mal geworfen und an jedem Pfad 0,5 also 1/2 keine Ahnung ob das so richtig ist

Beste Antwort und eine grobe Begründung dazu wird einen Stern verdienen..

Angenommen man schießt 5 mal mit einer Waffe, jeder schuss hat die wahrscheinlichkeit von 10% ein fehlschuss zu sein.

Wie würde die formel lauten um die wahrscheinlichkeit auszurechnen für genau einen fehlschuss, egal der wie vielte schuss es war?

und dann wie würde die formel aussehen dafür dass der fehlschuss an einer bestimmen stelle sein soll, also zum beispiel der 2. oder 4. oder was auch immer?

(bitte ohne binomialverteilung falls möglich)

Hi,

kurzgefasst, heute in der Schule sollten wir unter vielen Karten ein Ass ziehen, und wer es gezogen hat musste vorstellen. Am Ende waren nurnoch 2 Karten übrig, und das Ass wurde gezogen. Meine Freunde waren von der Überzeugung, der erste hätte eine geringere Chance gehabt, als der letzte. Ergibt das aber Sinn?

Die Chance, dass der erste eine gezogen hätte wäre z.B. 1 zu 20 gewesen. Der letzte der gezogen hätte, hätte eine Wahrscheinlichkeit von 19 zu 20 gehabt, dass einer davor schon das Ass gezogen hätte oder?

Ich bitte um eine richtige Erklärung.

Danke im Voraus!

Folgendes Szenario gilt: Es gibt eine Urne wo 4 Kugeln enthalten sind. 2x Schwarz 2x Rot. Nun zieht man hintereinander 2 Kugeln (ohne Zurücklegen). Nun will ich ausrechnen, wie viele verschiedene Ergebnisse es geben kann, die Reihenfolge der gezogenen Kugeln ist egal.

Um dies zu berechnen, müsste ich folgende Formel benutzen: n!/(n-k)!*k!

k=2, da ich ja 2 Kugeln ziehe.

Unsicher bin ich mir, was denn nun n ist. Setze ich für n=2 an (weil es 2 Farben gibt), so kommt als Menge der verschiedenen möglichen Ergebnisse 1 raus. Nutze ich n=4 (weil es 4 Kugeln gibt), so kommt als Menge der möglichen Ergebnisse 6 raus.

Beide Ergebnisse sind jedoch falsch. Stellt man sich den Versuch bildlich vor, so ist offensichtlich, dass die Menge der möglichen Ergebnisse 3 ergibt (Schwarz + Schwarz, Schwarz + Rot, Rot + Rot). Woran liegt das? Ist die obengenannte Formel für diesen Versuch nicht nutzbar und falls ja, welche Formel nutze ich stattdessen, um die Anzahl der möglichen Ergebnisse zu berechnen?

Die richtige Antwort sollte 2673 sein. Wie komme ich darauf?

Woher weiß ich wie viele Kombinationen es gibt mit 3 Würfeln maximal eine 9 zu Würfeln? Ich weiß, dass es 81 sind aber ich weiß nicht wie man darauf kommt.

Vielen Dank im Voraus

Beste Antwort + Begründung= Stern ⭐

Beste Antwort = Stern ⭐

Hallo zusammen vielleicht kann mir jemand ja weiterhelfen.

Ich dachte immer bei einer Wahrheitstabelle spielt die Reihenfolge der Eingänge keine Rolle weil es sich um boolsche Algebra handelt.

Aber in diesem Fall hab ich in einer Aufgabe den Eingang I2 als ersten Eingang in der Tabelle gelistet, dadurch ist das Endergebnis laut Lehrer leider falsch. Stimmt ihr dem zu?

Oben ist die Aufgabenstellung, unten meine Lösung. Ich könnte meine Note steigern falls ich etwas einzuwenden habe, ich hoffe ihr könnt mir Klarheit verschaffen. Vielen Dank!

Ein Zahlenschloss besitzt sechs Ringe, die jeweils die Ziffern 0, . . . , 9 tragen.

Wie viele Zahlencodes sind möglich, wenn die Ziffern der Größe nach geordnet sind? Warum sagt man hier :Kombination mit Wdh ?also die Formel n+k-1 über k

hier spielt doch die Reihenfolge eine rolle warum also keine Variation?

123456 ist doch was anderes als 112233

Ich blicks echt nicht sowas verwirrt mich jedes Mal

Wir sagen n ist die Anzahl an Steinen.

Wenn n alle vielfache von 6 sein kann( 6;12;24...), und es 2 Spieler gibt, die abwechselnd entweder die Hälfte ein Drittel oder zwei Drittel der Steine wegnehmen, für welche der Zahlen kann Spieler A (fängt an) gewinnen?( Wenn man keine Möglichkeit mehr hat, Steine wegzunehmen hat man verloren)

Meine Lösungsansätze:

Bei den meisten vielfachen von 6 ( z.B. 6;12;18) gewinnt A, allerdings gibt es auch Außnahmen, wie zum Beispiel 36. Warum?

4 Stelliges Passwort aus Ziffern und nicht mit 9 starten

3 Stelliges Passwort mit mindenstens 2 mal der Ziffer 3

Also ich hab mir das hier zur Hilfe genommen aber ich hab den Eindruck, ich interpretiere immer den Weg Zwischen liegt eine Auswahl vor beziehungsweise Kombination oder Variation mit Reihenfolge oder ohne Reihenfolge falsch.

hier einpaar Aufgabe : Gegeben seien die Ziffern 1 bis 9 (ohne die 0).

Wie viele vierstellige Zahlen können daraus gebildet werden?

Wie viele vierstellige Zahlen können daraus gebildet werden, so dass jede Ziffer ho ̈chstens einmal vorkommt.

Wie viele vierstellige Zahlen ko ̈nnen daraus gebildet werden,die durch 5 teilbar sind?

Wie viele vierstellige Zahlen können daraus gebildet werden, so dass die Ziffern der größe nach geordnet sind.

Kann mir jemand sagen, wie ich diese Aufgaben mithilfe der Bild gezeigten Struktur löse?

bei der ersten Aufgabe hätte ich jetzt gesagt : Auswahl Ja , die Reihenfolge der einzelnen Zahlen ist doch egal, oder? Und dann kommen Elemente mehrfach vor: nein

somit wär’s doch 9 über 4 das ist aber falsch.

Hallo,

folgende Aufgabe:

Bestimme die Zahl der Worte mit 4 Buchstaben, die man aus den Buchstaben des Wortes MORGENS bilden kann. Wie viele von ihnen enthalten beide Vokale?

Es gibt ja zwei Vokale in dem Wort, also dachte ich es müsste heißen:

2*4 * 1*3* 5*2* 4*1 Weil es 2 Vokale und vier Plätze gibt, dann einen Vokal und drei Plätze, dann 5 Konsonanten und 2 Plätze und schließlich 4 Konsonanten und ein Platz.

Die Lösung sagt aber 4*3*5*4. Wo liegt mein Denkfehler?
LG

Beste Antwort bekommt einen Stern (immer mit Begründung bitte)

Hallo, ich bin wahrscheinlich wieder etwas doof, ich komme leider nicht auf die Resultate...

8) komme ich gar nicht weiter

und bei 7c) dachte ich es sei 2^12 - 3 ist es jedoch nicht...

Lösungen: 8) 26; 7c) 4 017

Irgendwas stimmt nicht, Hilfe

Wir sagen n ist die Anzahl an Steinen.

Wenn n alle vielfache von 6 sein kann( 6;12;24...), und es 2 Spieler gibt, die abwechselnd entweder die Hälfte ein Drittel oder zwei Drittel der Steine wegnehmen, für welche der Zahlen kann Spieler A (fängt an) gewinnen?

( Wenn man keine Möglichkeit mehr hat, Steine wegzunehmen hat man verloren)

Guten Nachmittag,

ich habe noch ein paar Fragen zu dieser Aufgabe, die ich bearbeitet habe. Im folgenden befindet sich ein Bild der Aufgabe und zwei Bilder meiner bearbeiteten Aufgabe. Danach folgen meine Fragen.

• Habe ich die Berechnungen falsch bezeichnet?
• Ich habe ja immer p = … geschriebene, obwohl ja keine Wahrscheinlichkeit, sondern ein Anteil zu berechnen war.
• Wie muss man hier die Berechnungen bezeichnen?
• Einfach ohne Bezeichnung der Berechnung (also ohne z.B. wie hier „p“ rechnen)?

Ich freue mich über eure Hilfe.

Einen wunderschönen guten Morgen,

ist bei dieser Aufgabe der Lösungssatz von der Musterlösung falsch formuliert? Im folgenden befindet sich ein Bild der Aufgabe, ein Bild der Lösung und ein Bild meiner Rechnung mit meinen Lösungssatz. Danach folgen meine Fragen.

• In der Lösung steht ja, dass das in 91,08 % der positiv ermittelten Ergebnisse der Fall ist.
• Aber wenn doch schon ein Ergebnis positiv ermittelt wurde, also die A-Probe positiv ist, dann liegt die Wahrscheinlichkeit für eine positive B-Probe doch bei 99 %.
• Findet ihr den Lösungssatz in der Lösung auch nicht richtig formuliert?
• Wie würdet ihr den Lösungssatz formulieren?
• Ist mein Lösungssatz gut/besser als der in der Lösung?

Hi

Ich bin gerade am überlegen, wie hoch die Wahrscheinlichkeit ist, das in einem Kartendeck von 10 Karten mit 2 jokern die Joker hintereinander kommen?

(Wahrscheinlichkeitsrechnen ist ne Weile her bei mir)

Mein Ansatz war:

Beim ersten ziehen 2\10 * beim zweiten ziehen 1\9= 1\30=3,3%

Is das richtig?

Und wie verändert sich dash wenn ich das Deck verdoppelt?

Einen wunderschönen guten Abend,

meine Fragen beziehen sich auf folgenden Teil der Aufgabe (im Anhang der Frage befindet sich ein Bild von der Aufgabe, ein Bild von der Lösung und ein Bild von meinem Merkblatt):

Aus zehn Sportlern eines Kaders werden genau drei zur Dopingkontrolle ausgelost. Wie viele Möglichkeiten gibt es?

• Ich verstehe, dass hier die Reihenfolge keine Rolle spielt.
• Aber wieso handelt es sich bei diesem Aufgabenteil (siehe Zitat) um Ziehen ohne Zurücklegen?
• Wieso benutzt man hier die „Lotto-Regel“ (siehe mein Merkblatt)?
• Diese Namen bei dem Merkblatt hat mein Lehrer aus irgend einem alten Schulbuch entnommen und seitdem unterrichtet er das so, nicht das ihr euch wundert, woher diese Namen der Regeln überhaupt kommen.

Ich freue mich sehr auf eure ausführlichen Antworten.

Ein fairer roter und ein schwarzer Würfel werden auf einmal geworfen. Bestimme die Wahrscheinlichkeit

1. mit einem Würfel Sechs und mit dem anderen Würfel Eins zu werfen;

Stimm es wenn ich sag, die Sechs kann beim roten ODER schwarzen Würfel vorkommen, das heißt 1/6 +1/6 und für die Eins bleibt dann nur mehr ein Würfel übrig also (1/6 + 1/6) * 1/6

Hallo, wie berechne ich das, bzw welche Formel verwende ich hierfür:

Wie viele Partition mit 5 Teilen hat eine 11- elementige menge?

Danke

Welche Formel muss ich hierfür verwenden?

Welche Formel wird für diese Aufgabe verwendet?

Wie berechne ich das bzw. Welche Formel muss ich hier benutzen?

Hallo, wie berechnet man eine Partition?

Ich habe die Aufgabe: Wie viele Partition mit 5 Teilen hat eine 11 Elementige Menge? Gibt es dafür eine bestimmte Formel?

Ich möchte Wissen: handelt es sich um ein vereinbares oder ein unvereinbares Ereignis?

Ein fairer roter und ein schwarzer Würfel werden auf einmal geworfen. Bestimme die Wahrscheinlichkeit

1. mit entweder dem roten oder dem schwarzen Würfel Sechs zu werfend;

Hallo Ihr Lieben, ich brauche bitte Hilfe bei dieser Rechnung. Es geht um Binomialverteilung🫣die Aufgaben B und C ganz unten auf dem Zettel finde ich am schwierigsten, also die kleinen Buchstaben …. Vielleicht könnt ihr mir Ansätze geben, wie ich das einfach lösen kann, da ich das bis morgen haben muss. Das wär sehr nett..

danke

Guten Abend,

findet ihr, dass diese Wahrscheinlichkeitsaufgabe verständlich gestellt ist?

Ich kann die Aufgabe auf zwei verschiedene Weisen verstehen:

1. Der Bezahlautomat wählt durch Zufall zuerst aus, ob der Kunde bei seinem Kauf die Chance auf die Freikarte (20 % Chance) oder die Chance auf den doppelten Rabatt (50 % Chance) hat. Also der Automat wählt zuerst aus, ob der Kunde die Chance auf die Freikarte oder den doppelten Rabatt bekommt und dann bestimmt er danach nochmal durch Zufall, ob der Kunde das dementsprechende gewonnen hat oder nicht.
2. Wir stellen uns die Wahrscheinlichkeit bildlich mit einem Glücksrad vor, 20 % ist hierbei die Freikarte, 50 % ist hierbei der doppelte Rabatt und 30 % ist hierbei der normale Preis mit 20 % Jubiläumsrabatt.

Ich finde, dass die Aufgabe unverständlich gestellt ist, seht ihr es auch so? Wie versteht ihr die Aufgabe?

Mich interessiert c) und d) Wir haben gelernt bei der ODER Rechnung gibt es entweder vereinbare oder unvereinbare Ereignisse.

Hier bei c) hätte ich gesagt unvereinbar deswegen einfach 1/6 + 1/6 aber im Lösungsheft steht als Lösung 5/18

Guten Abend,

kann mir jemand bei dieser Aufgabe weiterhelfen? Eine genaue Erklärung würde mir unendlich viel helfen. :-)

Hey, ich komme bei folgender Aufgabe gerade nicht weiter, vielleicht kann mir ja jemand einen Ansatz liefern.

Eine andere Urne enthält ebenfalls einhundert Kugeln: für die Anzahl W der enthalten weißen Kugeln gilt 1<W<99. Auch aus dieser Urne werden zwei Kugeln nacheinander zufällig gezogen. Die erste gezogene Kugel ist weiß. Betrachtet werden zwei Fälle: 1. Fall: Die erste gezogene Kugel wird nicht zurücklegt, bevor man die zweite zieht. 2. Fall: Die erste gezogene Kugel wird zurücklegt, bevor man die zweite zieht. Die Wahrscheinlichkeit dafür, dass auch die zweite gezogene Kugel weis ist, beträgt im 1. Fall p, im 2. Fall ist sie 2 % von p größer. Berechnen Sie den Wert von W.

Danke!!

Einen wunderschönen guten Abend,

wo ist hier mein Denkfehler bei den Aufgaben e) und f)? Denn die Ergebnisse weichen von den der Lösung stark ab. Möglicherweise ist mein Rechenweg bei d) auch falsch und nur durch Zufall richtig. Es kann natürlich auch sein, dass die Lösung (teilweise) falsch ist.

Aufgabe:

Lösung:

Hilfreiche Informationen für euch, um diese Aufgabenstellung zu verstehen, falls ihr es so noch nicht kanntet. Denn es gibt ja die Unterschiede zwischen B(n;p(k)) und F(n;p(k)):

Eine Kombinatorik Aufgabe: Wie viele Möglichkeiten gibt es 8 Türme auf Schachfeld zu verteilen ohne, dass sie sich gegenseitig schlagen können? Folgendes Problem: Ich bin mir nicht sicher, ob ich hier mit der Subfakultät (!8) oder mit der Permutationsformel. Für !8 ist das Ergebnis 14833 Möglichkeiten und für die Permutationsformel 64P8. Welche Logik ist richtig?

Folgende Aufgabe :

15 Schüler werden in 3 Gruppen aufgeteilt. Eine Gruppe hat Montags, eine Dienstags und eine Mittwochs Sportunterricht. Jeder Schüler ist immer in genau einer Gruppe, die Reihenfolge innerhalb der Gruppe ist egal. Sage nun jeweils, wieviele Möglichkeiten es gibt, die Schüler auf die Gruppen aufzuteilen, wenn folgendes noch zusätzlich gilt:

im Sportunterricht am Montag sollen fünf, am Dienstag sechs und am Mittwoch vier Schüler unterrichtet werden

die drei Gruppen sollen gleich groß sein

Montag, Dienstag und Mittwoch sollen maximal sechs aber minimal 4 Schüler Sportunterricht haben

Hi, kann mir jemand erklären, wie man den K wert bei der Binomialverteilung bestimmt?

Was kommt in den Nenner bei der Formel? Was genau bedeutet das „m“?

Folgende Aufgabe bereitet mir Schwierigkeiten:

Bei einem Turnier werden zur Verringerung der Anzahl Spiele die 2 · n Mannschaften

(n ∈ N) in zwei gleich grosse Gruppen eingeteilt. Bestimme die Wahrscheinlichkeit

dafür, dass die beiden spielstärksten Mannschaften

a) in verschiedenen Gruppen oder

b) in der gleichen Gruppe sind.

Die Lösung lautet für a z.B. (n*(n-1)/2^n)

Mir ist klar, dass die Gesamtanzahl eine Mannschaft einer Gruppezuzuordnen 2^n ist, da jedes Team entweder in Gruppe 1 oder Gruppe 2 kann. (2 * 2 * ...)
Mir sind aber die günstigen Möglichkeiten für die zwei stärksten Teams nicht klar.
Wieso hat die eine Mannschaft n Möglichkeiten? Wiederrum dass die zweite Mannschaft davon -1 Möglichkeiten hat mach für die Aufgabe a) durchaus sinn, da die beiden nicht in eine Gruppe dürfen.

Ich danke für eine Rückmeldung und wünsche einen schönen Abend.

Hallo Zusammen,

ich wollte euch fragen, wie ich bei obenstehender Aufgabe auf folgende Lösung komme:

Ich danke euch für eine Rückmeldung.

Hallo Zusammen,

Ich habe eine Frage zur Kombinatorik:

Mir ist klar, dass jede Person mit "quasi" einer Person weniger anstosst. somit (n-1) + (n-2) + ... + 1.

Wenn ich nun die Summenformel von Gauss bilden möchte, dann muss ich meines Wissens letzter Wert + erster Wert der Reihe in die Klammer setzen und * der Anzahl Personen n rechnen und durch zwei dividieren:

(n(n-1 + 1)) /2. Die Lösung sieht aber wie folgt aus: (n(n-1))/2 <- weshalb wird/kann der letzte Wert der Reihe weggelassen werden?

Hallo Zusammen,

Zur folgenden Aufgabe habe ich die Fragen (Die Lösungen sind unten angefügt):

a) angenommen wir haben keinen Rohling als Rest. D.H. wir brauchen z.B. n=3 Rohlinge, also 2 gehen kaputt und nur der letzte, dritte kann gemäss Aufgabenstellung verwendet werden.
So wäre meiner Meinung nach die Formel (1-p)^2 * p. In der Lösung ist allerding die Allgemeine Lösung für 0 Rohlinge als Rest (1-p)^n-1. Setze ich nun mein n=3 ein so erhalte ich auch (1-p)^2, allerdings verstehe ich nicht ganz weshalb die Wahrscheinlichkeit des brauchbaren Stückes nicht dazumultipliziert werden muss?

Bei einem Rohlin rest allerdings sieht die Formel wie folgt aus (1-p)^n-2*p

b) ist wiederrum klar, da es z.B. bei zwei verwendeten Rohlingen nur einen brauchbaren gibt und einen nicht brauchbaren p(1-p)

Ich danke für eine Rückmeldung und wünsche einen schönen Nachmittag

Wenn eine Münze von 3 Würfen 2x davon auf der selben seite landet. Wieso ist dann die wahrscheinlichkeit dafür 3/4.

Ich hätte gesagt: Beim ersten werfen ist die WS 1/2 beim 2. Wurf wieder da sich die WS ja nicht verändert und beim letzten Wurf auch wieder 1/2...

Hallo, mir fehlen bei der Aufgabe die zwei blauen Prozentsätze. Wie kommt man auf die? Ich bitte um Hilfe.

Hallo, ich wollte fragen, ob mir jemand bitte relative und ansulute Häufigkeit in der Wahrscheinlichkeit erklären kann.

Danke!

Was ist die Wahrscheinlichkeit, dass ein in einer zufällig sortierten Playlist mindestens ein Song auf genau den Song folgt, auf den er auch in der originalen Playlist folgt?

z. B. mit 3 Songs und der Playlist 123

gäbe es

• 123 (12 und 23)
• 231 (23)
• 312 (12)

bei denen das zutrifft und

• 132
• 213
• 321

bei denen das nicht zutrifft, also wäre die Wahrscheinlichkeit 50%.

Was ist die Wahrscheinlichkeit, wenn die Playlist n Songs enthält? Kann man das überhaupt berechnen?

Wieso kommt bei der a) 1/100 raus?

ich komme auf 1/1000 wegen 1/10 * 1/10 * 1/10

Hallo Leute, ich habe hier 2 Aufgaben, dessen Lösungen mit den Urnenmodellen berechnet werden sollen. Leider weiß ich nicht genau welche ich anwenden sollte, und wie ich diese damit berechne..

1) Von 100 Personen werden in einer anonymen Befragung die Geburtsmonate festgestellt. Wie viele Ergebnisse sind in einer solchen Befragung möglich?

2) Bei einer Olympiade spielen 12 Tischtennismannschaften bestehend aus jeweils 3 Spielerinnen um die Goldmedaille. In jeder Mannschaft wird eine Spielführerin gewählt. Wie viele Möglichkeiten gibt es, dass genau in einer Mannschaft die älteste Spielerin gewählt wird?

Ich vermute, das bei Aufgabe 1, dass 4. Urnenmodell angewendet werden muss. Bei Aufgabe 2, dort tippe ich auf das Urnenmodell 1. Aber wie genau setze ich das jetzt um? Ich komme da leider nicht weiter

Hallo,

ich habe leider ein großes Problem. Ich gehe jetzt in die 11. Klasse (bayern) auf eines Privatgymnasiums. Davor habe ich bis zur 10. Klasse die Mittelschule (bayern) besucht und habe einfach sehr viele Lücken. Die Oberstufe ist so gekommen wie ich es erwartet hatte, alles geht schnell und jede Stunde kommt etwas neues dazu, ohne die davorige Stunde zu verstehen.

Jetzt bin ich an der Hälfte des ersten Halbjahres angekommen und ich habe komplett den Faden verloren. Übermorgen schreibe ich meine erste große Klausur und auch letzte große Klausur in diesem Halbjahr und ich weiss nicht was ich machen soll. Ich bin total überfordert, ich sitze im Unterricht und verstehe nichts!

Ich brauche dringend Hilfe, wie kann ich die Themenbereiche:

Lineare Funktionen, Quadratische Funktionen, Nullstellenform, Parameter, Potenzfunktionen, Limes, Ganzrationale Funktionen, Kombinatorik

alles lernen um mehr als 0 Punkte zu schaffen?

Soll ich von alles die Basics beherrschen oder was könnt ihr mir empfehlen um wenigstens 1Punkt oder mehr zu erreichen.

schonmal vielen dank für die aufmerksamkeit :)

Wie im Titel eigentlich schon gesagt habe ich mich gefragt, ob es möglich ist unendlich viele Häuser vom Nikolaus miteinander zu verbinden - sozusagen also ein Muster zu finden, womit man unendlich viele Häuser vom Nikolaus zeichnen kann - ohne seinen Stift hochzuheben oder eine Linie zweimal zu zeichnen. Hierbei würde ich mich nicht damit beschränken, dass die einzelnen Häuser direkt nebeneinander sein müssen, man könnte also auch die untere rechte Ecke des einen Hauses mit dem Dach des nächsten verbinden. Danke im Voraus :)

Hi, sorry ich bin echt schlecht in Mathe und schaffe es nicht meine Frage im Onlinetool dafür korrekt einzugeben, daher: vielleicht wollt/könnt ihr mir die Lösung sagen? (Der Lösungsweg ist mir dabei nicht wichtig, den würde ich eh wieder vergessen oder sogar nicht verstehen).

Es sind 6 Ziffern vorgegeben, die auch in richtiger Reihenfolge. Aber: irgendwo dazwischen oder davor oder dahinter muss eine weitere Ziffer eingefügt werden. Die kann von 0-9 alles sein. Nur zu Anfang könnte es keine 0 sein.

3franzosen, 7 deutsche, 10 briten. wie hoch ist die wahrscheinlichkeit, dass

a) 2 franzosen

b) 1 brite und 1 deutscher

ausgelost werden.

Wisst ihr wie ich dazu ein baumdiagramm mache und berechne?

Ich wollte ich euch fragen, wie man bei folgender Aufgabe auf die Lösung 14!/(3!*3!*2!*2!*2!*2!) * 1/(2!*4!) kommt.

Wie viele Möglichkeiten gibt es, 14 Personen in 6 Gruppen aufzuteilen, von denen 2 je 3 Personen und die restlichen 4 je 2 Personen enthalten?"

Der Teil mit "14!/(3!*3!*2!*2!*2!*2!)" ist klar, aber wie kommt man auf "* 1/(2!*4!)"?
Ist meine Annahme korrekt, das mit dem "zweiten" Teil die Möglichkeiten der Andordnung der einzelnen Gruppen aufgehoben wird?

Ich danke für eine Rückmeldung :)

Hallo Zusammen,

kann mit bitte Jemand bei folgender Kombinatorik Aufgabe helfen, wie man auf die Lösung 56 kommt?

"Drei nicht unterscheidbare Würfel werden geworfen. Wie viele verschiedene Augenkombinationen gibt es?"

Meiner Meinung nach können bei einem Wurf sechs verschiedene Seiten/Zahlen geworfen werden. Das würde aber bei drei Würfen 6^3 machen?

Gefragt ist das hier (siehe Bild)

"wie viele verschiedene Wurfbilder gibt es, bei 3 roten, 4 schwarzen und 2 blauen Würfeln?"

Das heisst, wie viele Farbanordnungen gibt es, also:

blau-rot-rot-schwarz-schwarz-blau-schwarz-rot-schwarz

oder

rot-schwarz-schwarz-blau-rot-schwarz-blau-rot-schwarz

Kann mir jemand den Lösungsweg geben?

Folgendes:

5 grüne Kugeln (G)

3 rote Kugeln (R)

2 schwarze Kugeln (S)

Aufgabe

Zeigen Sie, dass P(R) > (P(G))^2 gilt.

Wie gehe ich hier vor?

Die Wahrscheinlichkeit P(R) = 0,3

Aber wie mache ich weiter?
Vielen Dank im Voraus..

An einer Uni studieren 600 Studentinnen und Studenten. Der Rektor behauptet, dass es min- destens zwei Studierende geben muss, deren Vornamen und deren Nachnamen mit jeweils demselben

Buchstaben anfangen. Hat er recht

Es gibt doch 26 × 26 Kombination für Anfangsbuchstabe das vor und Nachnamens . Das wäre mein Ansatz weiter weiß ich leider auch nicht.

Ich habe eine Frage zu dieser Aufgabe. Die Lösung sagt bei Ansatz 3 und 4, dass die 10bzw. 5 über 3 die Anzahl der Möglichkeiten berücksichtigt. Also ist dies ein Ziehen ohne Zürücklegen mit Reihenfolge , oder ? Warum rechnet man aber nicht 5! in dem Fall. Liegt das daran, dass einmal 3 Pakete und einmal 2 Pakete die Gleichen sind ? Und wie würde man auf diese 5 über 3 kommen ? Ist bisschen länger diese Frage aber ich danke schon mal für die Antwort.

In einem Klassenzimmer befinden sich 15 (unterscheidbare) Tische mit jeweils 2 (unterscheidbaren) Sitzplätzen. Wie viele Sitzordnungen gibt es für 24 Schüler*innen, wenn niemand alleine an einem Tisch sitzen soll? 

Ich weiß, wie es funktioniert, habe da aber eine Frage. Und zwar türkis geht ja über den Rand hinaus. Werden B und D auch zur Vereinfachung gezogen, oder nur C?

Hallo, kann einer mir vielleicht schnell für die Teilaufgabe C und D einen Ansatz geben, wie man die Anzahl an Möglichkeiten berechnen könnte? Ich bräuchte es bis morgen dringend. Danke im Voraus!

Wieso hat sie immer 1:n genommen, aber aufeinmal dann 1:m? Ergibt für mich wenig Sinn.Ist es dasselbe, und wenn ja, warum nimmt sie dann nicht wieder 1:n , so wie bei den Orten wo ich eine 2 in rot makiert habe.

Für "keine Ziffer doppelt" habe ich es so gerechnet:

6-stellige Zahl = 10^6 Möglichkeiten

6 stellige Zahlen ohne doppelte Ziffer = 10*9*8*7*6*5 = 151.200 Möglichkeiten

Und 151200 / 10^6 = 0,1512

Für genau eine Ziffer doppelt brauche ich dann ja die Möglichkeiten für 6 stellige Zahlen mit einer doppelten Ziffer. Da habe ich aber keine Ansatz, wie man darauf kommt. Danke für die Hilfe.

Hallo Zusammen,

Kann mir bitte jemand bei folgender Aufgabe erklären, wie A2, und A3 aussehen?
A1 ist mir klar, da ich hier mit Bit 1 = v starten kann und somit A1 = [(v,v,v),(v,r,r),(v,r,v),(v,v,r)] erhalte.
Aber wie komme ich nun auf A2 und drei? Beim Baumdiagramm müsste man bei Bit 2 starten und quasi Bit 1 auslassen? z.B. A2 = [(*,v,r)(*,v,v)]

Hallo, ich habe hier ein Baumdiagramm vorgegeben (siehe Bild). Ich muss das Baumdiagramm auch ergänzen. Aber wie komme ich auf die Ergebnisse im Baumdiagram bei der gelben, dunkelblauen und schwarzen Kugel?

Also ich hab da paar Verständnisprobleme wegen dieser Aufgabe :

Ich muss den geschlossenen Ausdruck finden, nach Recherche soll das ein einfacher Ausdruck sein mit dem man für eine Variable eine Zahl einsetzt und gleich den Ausdruck ausrechnen kann.

Nun verstehe ich nicht warum ich nicht einfach die Summenformel nehmen kann, sondern den Fehler berechnen muss. Und muss ich nachdem ich den Fehler berechnet habe noch was anderes berechnen oder ist das das Ergebnis? Falls es von Wichtigkeit ist das ist für mein Kombinatorik-Modul. Würde mich über jegliche Hilfe freuen

Guten Abend,

kann mir hier jemand bei der Aufgabe weiterhelfen?

Folgende Frage/Überlegung ist mir bereits aufgekommen:

• Bei a) denke ich, dass es ziehen ohne zurücklegen ist. Jedoch weiß ich nicht, ob die Reihenfolge berücksichtigt wird oder nicht. Woran erkenne ich das? Ich brauche dafür dringend Beispiele womit ich mir das merken kann, ob etwas mit oder ohne Berücksichtigung der Reihenfolge ist. Daher habe ich diese Frage hier gepostet, um das für immer zu verstehen.

Ich freue mich über eure Antworten.

Hallo zusammen

Warum ist die Wahrscheinlichkeit bei Gewinn 0, -1 bei 3/8? Dachte die wäre auch bei 1/8 weil die Wahrscheinlichkeit ja 1/2 × 1/2 × 1/2 ist?

Könnte mir das jemand erklären?

Danke☺

Bei einem Spiel mit Buchstaben Karten werden die Buchstaben des Wortes SOLO

ungedreht und vermischt.

Es werden 3 Karten hintereinander aufgedeckt und deren Buchstabe jeweils notiert.Nachdem eine Karte gezogen wurde, wird diese zurückgelegt, umgedreht und die Karten vermischt.

1. zeichne das dazugehörige Baumdiagramm
2. wir groß ist die Wahrscheinlichkeit, dass der Reihe nach das Wort LOS entsteht

Guten Abend,

im Folgenden habe ich ein paar Fragen zu der Aufgabe 3. Gebt mir gerne zusätzlich auch eine Rückmeldung, ob meine Ansätze richtig sind.

Aufgabenteil a)

• was ist bei der Aufgabe 3a) die Ergebnismenge? Muss ich alle möglichen Pfade berücksichtigen, also mit Berücksichtigung der Reihenfolge oder ohne Berücksichtigung der Reihenfolge?

-> Ohne Berücksichtigung der Reihenfolge wäre es S = {KKK; KKZ; KZZ; ZZZ}

-> Mit Berücksichtigung der Reihenfolge wäre es S = {KKK; KKZ; KZK; KZZ; ZKK; ZKZ; ZZK; ZZZ}

Aufgabenteil b)

Hier würde ich folgendes schreiben:

Xe {0; 1; 2; 3}

• Muss man das „e“ nach dem x schreiben?

Aufgabenteil c)

Wie muss ich hier den Wert für X angeben?

• Reicht es so:

P(x=2) = 0,4^2 * 0,6 = 0,096 = 9,6 %

• oder muss man es so angeben:

Xe {2}

• Wo ist der Unterschied? Was ist richtig?

Aufgabenteil d)

P(x>2) = 0,4^3 = 0,064 = 6,4 %

• Wie kann man dieses Ereignis auf zwei verschiedene Arten in Worten beschreiben?

Aufgabenteil e)

E: Es fällt genau zweimal Zahl.

Ē: Es fällt genau dreimal oder weniger als zweimal Zahl.

Unter einer Warenladung von 12 Containern sind drei mit Schmuggelgut.

Wie groß ist die Wahrscheinlichkeit dafür, dass beim Offnen

1. von 3 Containern keiner mit Schmuggelgut dabei ist,

meine Antwort:

75 % da 25 % geschmuggelt sind.

2 von 3 Containern genau zwei ohne Schmuggelgut dabei ?

kein Plan

Guten Mittag,

meine Frage bezieht sich auf die Aufgabe 4 c).

4c)

Berechnet werden soll ja die Anzahl der möglichen Ergebnisse, bei denen die Augenzahlen verschieden sind.

Beim ersten Würfel kann noch jede Zahl drankommen, also gibt es 6 Möglichkeiten. Beim zweiten Würfel können noch 5 Zahlen drankommen. Beim dritten Würfel können noch 4 Zahlen drankommen. Beim vierten Würfel können noch 3 Zahlen drankommen. Beim 5. Würfel können noch 2 Zahlen drankommen.

Also berechne ich:

p = 6 * 5 * 4 * 3 * 2 = 6!/1! = 720 Möglichkeiten.

Wieso steht in der Lösung aber:

p = 6! = 6 * 5 * 4 * 3 * 2 * 1 = 720 Möglichkeiten?

Zwar ist das Ergebnis gleich aber es gibt doch nur 5 Würfel und in der Lösung werden 6 Zahlen multipliziert. Ist der Ansatz in der Lösung richtig?

Guten Tag,

meine zusammengefassten Fragen (Lediglich 3 Stück: 1., 2., 3.) befinden sich weiter unten zwischen den Hastags eingeschlossen.

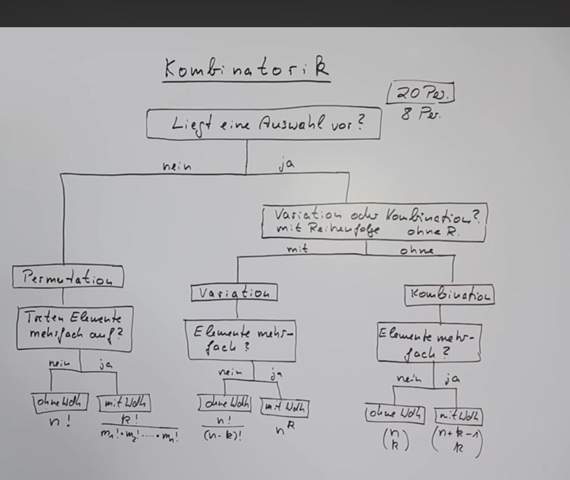
Ich frage mich, was der Unterschied zwischen der „nCr“-Taste und der „nPr“-Taste ist, also wenn man den Binomialkoeffizienten im Taschenrechner berechnet.

• Die „nCr“-Taste wird ja benutzt, wenn die Reihenfolge egal ist. C -> Combinations (= Kombinationen).
• Die „nPr“-Taste wird ja benutzt, wenn die Reihenfolge beachtet wird. P -> Permutations (= Permutationen).

Doch was rechnet der Taschenrechner anders, wenn ich die „nCr“-Tase bzw. die „nPr“-Taste verwende? Hierfür habe ich im Folgenden ein paar Beispiele gemacht, um es zu verstehen:

• (1)

5 nCr 0 = 1

5 nPr 0 = 1

• (2)

4 nCr 2 = 6

4 nPr 2 = 12

• (3)

6 nCr 2 = 15

6 nPr 2 = 30

• (4)

4 nCr 3 = 4

4 nPr 3 = 24

• (5)

6 nCr 3 = 20

6 nPr 3 = 120

• (6)

8 nCr 3 = 56

8 nPr 3 = 336

• (7)

5 nCr 4 = 5

5 nPr 4 = 120

• (8)

7 nCr 4 = 35

7 nPr 4 = 840

• (9)

9 nCr 4 = 126

9 nPr 4 = 3.024

Feststellungen zu den Beispielen:

• Bei den Beispielen (1)-(3) verdoppelt sich das Ergebnis bei der Verwendung der „nPr“-Taste im Vergleich zur „nCr“-Taste einfach, da es doppelt so viele Möglichkeiten gibt, für zwei gleiche Sachen, wenn die Reihenfolge berücksichtigt wird.
• Bei den Beispielen (4)-(6) versechsfacht sich das Ergebnis immer, wenn man die „nPr“-Taste statt der „nCr“-Taste verwendet.
• Bei den Beispielen (7)-(9) vervierundzwanzigt sich das Ergebnis immer, wenn man die „nPr“-Taste statt der „nCr“-Taste verwendet.

############################

1. Nun frage ich mich, was sich bei der Berechnung beim Taschenrechner verändert, wenn statt der „nCr“-Taste die „nPr“-Taste verwendet wird und umgekehrt. Könnt ihr mir das sagen, was der Taschenrechner da anders berechnet?
2. Wieso ist immer die Veränderung im Vielfachen in meinen Beispielen (1)-(3); (4)-(6); (7)-(9) gleich, wenn ich statt der „nCr“-Taste die „nPr“-Taste verwende? Gibt es dafür eine Begründung?
3. Wieso kommt bei Beispiel (1) immer 1 raus? Wieso kommt immer 1 raus, wenn unten im Binomialkoeffizient 0 steht? Kann mir dafür jemand ein einfaches Beispiel in Form einer „Aufgabe“ geben?

############################

Beispiel zur Verwendung der „nCr“-Tase im Taschenrechner:

Paul, Julian, Fritz und Thomas möchten zusammen Tennis spielen. Wie viele Möglichkeiten für Zweierteams gibt es (Die Reihenfolge der Nominierung der Spieler in den Teams ist egal)?

Hierbei gibt es ja 4 über 2 Möglichkeiten, also den Binomialkoeffizienten (4 2). Hier verwenden wir nCr, da die Reihenfolge nicht berücksichtigt wird. Es ist also egal, ob für ein Zweierteam zuerst der eine Spieler oder erst der andere Spieler nominiert wird.

4 nCr 2 = 6

Beispiel zur Verwendung der „nPr“-Tase im Taschenrechner:

Paul (1), Julian (2), Fritz (3) und Thomas (4) möchten zusammen Tennis spielen. Es werden Zweierteams gebildet. Beide Nummern der Spieler bilden zusammen eine zweistellige Zahlenfolge (Beispiel: Paul (1), Julian (2) = 12 ≠ Julian (2), Paul (1) = 21). Wie viele verschiedene Zahlenfolgen gibt es?

4 nPr 2 = 12

Guten Abend,

ich benötige Hilfe bezüglich der Binomialkoeffizienten und zum Verständnis zur Verwendung von nCr und nPr. Wenn ihr mir eine Antwort hinterlassen möchtet, so geht am besten auf jeden der Punkte mit Nennung des Punktes (1., 2., 3., 4., 5.) ein. :-) Das würde mir perfekt helfen und ich werde es dann hoffentlich endlich verstehen. Am besten wäre eine Antwort mit einer super leicht verständlichen Erklärung :-)

Ich freue mich über eure Antworten.

1. Wieso sind immer (?) zwei Binomialkoeffizienten gleich, bei denen sich nur die untere Zahl unterscheidet?
2. Wieso ist (5 4) also 5 nCr 4 das gleiche wie (5 1) also 5 nCr 1? Beides Mal kommt 5 raus.
3. Das gleiche gilt für (32 31) also 32 nCr 31 und (32 1) also 32 nCr 1. Beide Male kommt 32 raus.
4. Welche Rechnung steckt hinter nCr und welche Rechnung steckt hinter nPr und wo sind die Unterschiede hinsichtlich der „Formel“ und der Verwendung von „nCr“ und „nPr“?
5. Gibt es diese Gleichheit von zwei verschiedenen Binomialkoeffizienten auch bei der Rechnung mit nPr? Oder gibt es das nur bei der Rechnung mit nCr wie oben bei Punkt 2 und 3 in meinen Beispielen?

Hey,

ich mache bei der langen Nacht der Mathematik mit, und in einer Aufgabe geht es darum, zu berechnen, wie viele verschiedene Dodekaeder-Würfel es gibt.

(Dodekaeder sind Würfel, die aus zwölf gleichseitigen Fünfecken bestehen. Ihre Seitenflächen sind dann mit den Zahlen von 1 bis 12 beschriftet, deren gegenüberliegende Seiten die Summe 13 ergeben).

Was ist hier die Lösung und wie berechnet man das?

Danke schonmal

An einem Fußballturnier nehmen 12 Mannschaften teil. Wie viele Endspielpaarungen sind theoretisch möglich und wie viele im Halbfinale?

Vielleicht könnt ihr mir weiterhelfen