Probleme bei Kombinatorik Aufgaben?
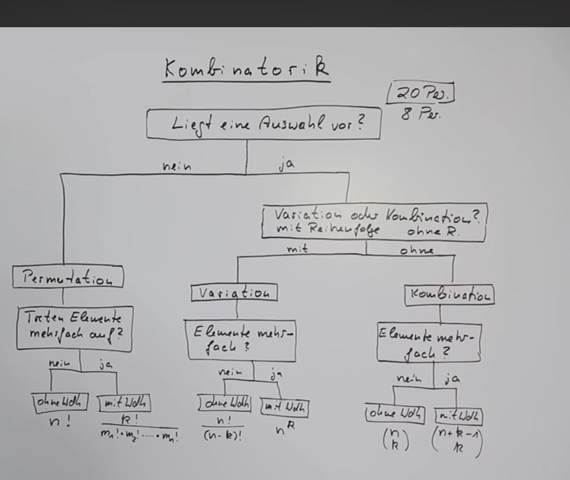
Also ich hab mir das hier zur Hilfe genommen aber ich hab den Eindruck, ich interpretiere immer den Weg Zwischen liegt eine Auswahl vor beziehungsweise Kombination oder Variation mit Reihenfolge oder ohne Reihenfolge falsch.
hier einpaar Aufgabe : Gegeben seien die Ziffern 1 bis 9 (ohne die 0).
Wie viele vierstellige Zahlen können daraus gebildet werden?
Wie viele vierstellige Zahlen können daraus gebildet werden, so dass jede Ziffer ho ̈chstens einmal vorkommt.
Wie viele vierstellige Zahlen ko ̈nnen daraus gebildet werden,die durch 5 teilbar sind?
Wie viele vierstellige Zahlen können daraus gebildet werden, so dass die Ziffern der größe nach geordnet sind.
Kann mir jemand sagen, wie ich diese Aufgaben mithilfe der Bild gezeigten Struktur löse?
bei der ersten Aufgabe hätte ich jetzt gesagt : Auswahl Ja , die Reihenfolge der einzelnen Zahlen ist doch egal, oder? Und dann kommen Elemente mehrfach vor: nein
somit wär’s doch 9 über 4 das ist aber falsch.
1 Antwort
Erst einmal: Auch bei Permutationen liegt eine Auswahl vor - der erste Punkt mach keinen Sinn. Es sollte besser heißen: "Wird gezogen?".
1. Variation: Es wird gezogen (nach dir: Es gibt eine Auswahl), nämlich Ziffern aus der Menge {1, 2, 3, 4, 5, 6, 7, 8, 9}. Es kommt auf die Reihenfolge an, denn jede Permutation von vier Ziffern ergibt eine andere Zahl (z. B. ist 1234 ≠ 4321 oder 1122 ≠ 1212). Ob es mit/ohne Wiederholung ist, wissen wir streng genommen nicht - es steht dort nur, dass wir die Ziffern gegeben haben, aber nicht, ob wir sie nur einmal verwenden dürfen. Allerdings gehe ich davon aus, dass wir sie öfters verwenden dürfen, da "Ziffern" erst einmal öfters vorkommen können. Demnach erhalten wir 9⁴ Variationen.
- gibt es dann für Permutation auch andere Formeln?
- wenn du sagst, es sollte heißen, wird gezogen? Darunter kann ich mir bei der Aufgabe zum Beispiel gar nichts vorstellen. Ich ziehe ja keine Zahlen oder so
- die letzten zwei Aufgaben könntest du du mir da auch helfen? wüsste jetzt nicht wie ich die löse mithilfe der Struktur
- Den Rest hab ich verstanden. Danke
gibt es dann für Permutation auch andere Formeln?
Meines Wissens nach nicht.
Bei (1.) handelt es sich aber um eine Variation, nicht um eine Permutation.
Und der Unterschied von Variation zu Kombination ist eben, dass die Reihenfolge eine Rolle spielt: Eine Kombination ist äquivalent zu der Menge an Variationen, die Permutationen der Kombination sind, Bsp.: 1233 und 3213 sind zwei Variationen, aber nur eine Kombination. 1233 ist also eine Permutation von 3213 und umgekehrt. Wenn dich das veriwrrt, denk dir einfach nur, dass die Reihenfolge bei Zahlenziffern eine Rolle spielt.
Man kann für jede der vier Plätze neun verschiedene Ziffern einsetzen, also gibt es 9⁴ Variationen.
wenn du sagst, es sollte heißen, wird gezogen? Darunter kann ich mir bei der Aufgabe zum Beispiel gar nichts vorstellen. Ich ziehe ja keine Zahlen oder so
Stimmt, du ziehst keine Zahlen. Du ziehst Ziffern, die Zahlen bilden.
"Ziehen" darfst du dir nicht zu wörtlich vorstellen. Stell es dir so vor:
Du hast eine Menge {1, 2, 3, ..., 9} und ziehst (wählst) aus dieser eine Zahl (Ziffer). Die "gezogene" Zahl wird wieder aufgefüllt, sodass die Menge immer gleich bleibt.
Das machst du für die zweite Ziffer auch so usw.
Insgesamt erhälst du also für die erste Ziffer neun Möglichkeiten, für die zweite auch usw., also 9•9•9•9=9⁴ Möglichkeiten (Variationen).
die letzten zwei Aufgaben könntest du du mir da auch helfen? wüsste jetzt nicht wie ich die löse mithilfe der Struktur
2. Jede Ziffer (der vierstelligen Zahl) kann höchstens einmal vorkommen.
Du ziehst wieder aus der Menge {1, 2, 3, ..., 9}. Bei Zahlen kommt es auch auf die Reihenfolge an => Es handelt sich um Variationen.
Nun kann jede Ziffer nur höchstens einmal vorkommen, also ohne Wiederholung.
Wir erhalten also 9!/(9–4)! Möglichkeiten (Variationen).
3. Das ist schon schwieriger.
Die erste Ziffer, nennen wir sie k, ist frei wählbar. Für die zweite gibt es dann nur noch k Möglichkeiten. Nennen wir diese Ziffer l. Für die dritte Ziffer gibt es also nur noch l Möglichkeiten. Nennen wir diese Ziffer i. Für die letzte Ziffer gibt es dann nur noch i Möglichkeiten.
Für k, l und i musst du jetzt nacheinander die Ziffern 1 bis 9 einsetzen, wobei l höchstens k und i höchstens l sein muss.
Wir erhalten also 495 Möglichkeiten (Formel kann ich schlecht darstellen, brauche Summenzeichen dafür).
Das entspricht aber keinen der oben genannten Fälle: Es ist eine spezielle Auswahl an Variationen.
Zur 3. Aufgabe noch der Rechenweg:
Wenn die dritte Ziffer n ist, dann gibt es für die vierte Ziffer n Möglichkeiten.
sum{i=1, n}[1]
Für n gibt es m Möglichkeiten, wenn m die zweite Ziffer ist, also sind wir für die letzten beiden Ziffern schon bei
sum{n=1, m}[sum{i=1, n}[1]]
Möglichkeiten. Für m gibt es k Möglichkeiten, wenn k die erste Ziffer ist, also sind wir schon bei
sum{m=1, k}[sum{n=1, m}[sum{i=1, n}[1]]]
Möglichkeiten. Zuletzt gibt es für k genau 9 Möglichkeiten, also erhalten wir insgesamt
sum{k=1, 9}[sum{m=1, k}[sum{n=1, m}[sum{i=1, n}[1]]]] = 495
Möglichkeiten, vierstellige Zahlen mit den Ziffern 1 bis 9 nach ihrer Größe nach zu sortieren.