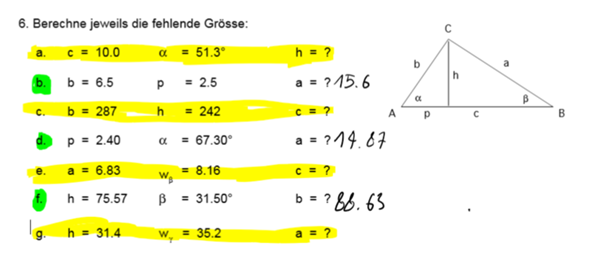
Tan, Cos, Sin Aufgabe?
Hallo zsm
Bei dieser Aufgabe konnte ich a, d und f richtig ausrechnen. Bei allen Gelb markierten (a, c, e, g) kam ich nicht mehr weiter. Ich habe das ganze zwar ausgerechnet, genau wie bei den anderen auch, aber meine Resultate stimmen nicht mit denen in den Lösungen überein. Kann mir da jemand helfen? Entweder schnell ausrechnen aus was ihr kommt, sodass ich bestätigen kann ob ich es falsch gemacht habe, und wenn es möglich wäre auch ein Rechnungsweg zu zeigen, da wäre ich sehr dankbar. Das ganze soll mit cos, sin und tan gerechnet werden.