Modellieren periodischer Vorgänge? Sinus- u. Kosinusfunktion?
Wer kann da bei diesem Thema helfen und dafür eine Beispielaufgabe mit Lösung schicken? Gerne auch mehr ;)
Schulstoff für 10. Klasse Gymnasium Niedersachsen
1 Antwort
"Jedes Jahr werden auf Gutefrage.net Fragen zu den immer gleichen Schulinhalten gestellt, weil jedes Jahr Schülerinnen und Schüler die immer gleichen Rahmenlehrpläne ihres jeweiligen Jahrganges durchlaufen. Es zeigt sich, dass der Anteil an jährlich auftretenden schulischen Fragen, die mithilfe der Suchfunktion beantwortet werden könnten, an einem Stichtag in den Sommerferien am 1. August mit 20% am geringsten ist (Tag 213 von 365 Jahrestagen). Im Winter am Tag 30,5 von 365 ist der Anteil hingegen mit 80% maximal.
Aufgabe: Geben Sie eine mögliche Funktionsgleichung an, die den Anteil solcher Fragen sinusartig als Funktion der Jahrestage beschreibt."
Zunächst die allgemeine Funktionsgleichung der gewünschten Funktion aufschreiben und sich über die verschiedenen Parameter bewusst werden:
f(x) = a ⋅ sin(b ⋅ (x ⋅ c)) + d
x - Jahrestag
f(x) - Anteil zum Tag x
c - verschiebt die Funktion entlang der x-Achse
b - bewirkt eine Verkleinerung (b größer als 1) oder Vergrößerung (b kleiner als 1) der Wellenlänge.
d - Lage der Ruhelage (Wert auf der y-Achse um welche f(x) oszilliert)
a - Beeinflusst die maximale Auslenkung aus der Ruhelage.
Bei dem Beispiel oszillieren die Anteile zwischen 20% und 80%. d entspricht also 50%:
f(x) = a ⋅ sin(b ⋅ (x + c)) + 0,5
Darüber hinaus kennen wir 2 Punkte:
(30,5 | 0,8) und (213 | 0,2)
Wir stellen uns vor wie der Graph der Sinus-Funktion (sin(x)) verläuft:
0: 0
π/2: 1
π: 0
3 π/2: -1
2π: 0
Sowohl beim Minimum, als auch beim Maximum beträgt der Betrag des Funktionswertes Eins (+1 beim Maximum, -1 beim Minimum). Wenn wir den Term sin(b ⋅ (x + c)) betrachten, ist auch dessen Betrag, egal ob am Tag 30,5 oder am Tag 213, Eins. Beim Minimum muss folglich 0,3 von 0,5 abgezogen werden um 0,2 zu erhalten und beim Maximum muss 0,3 zu 0,5 hinzuaddiert werden um 0,8 zu erhalten, d.h. a beträgt 0,3.
f(x) = 0,3 ⋅ sin(b ⋅ (x + c)) + 0,5
c beschreibt, wie weit die Funktion gegenüber der nicht-verschobenen Sinusfunktion entlang der x-Achse verschoben ist. Eine Verschiebung um c nach rechts, entspricht hierbei einem Wert von -c (minus!).
Angenommen wir betrachten eine Funktion, die ebenfalls auf unser Beispiel zugeschnittene Werte von a, b und d besitzt, aber nicht verschoben ist. Die erste Periode läuft dann von Tag 0 bis Tag 365. Und das erste Maximum würde bei Tag 90 erreicht (90 Tage sind 25% von 360, genauso wie π/2 25% von 2π sind). Unser Maximum soll aber bei Tag 30,5 liegen. D.h. c beträgt 59,5 (weil 90 - 59,5 = 30,5).
f(x) = 0,3 ⋅ sin(b ⋅ (x + 59,5)) + 0,5
Der Term (x + c) innerhalb des Ausdrucks sin() ist nun bekannt. Die Funktion sin() "weiß" aber nichts von der jeweiligen Textaufgabe, d.h. ob wir mit Tagen, Meter, Stunden usw. rechnen und wie groß unsere Wellenlänge sein soll. sin() nimmt lediglich Vielfache von Werten zwischen 0 und 2π entgegen und ordnet diesen Werte zwischen -1 und 1 zu. b dient im Sachbeispiel eben diesem Zweck, der Überführung von Werten auf "unserer Skala" in Werte auf einer Skala von 0 bis 2π. b beträgt also
360 Tage entsprechen dann 2π. Damit haben wir insgesamt
f(x) = 0,3 ⋅ sin(2⋅π ⋅ 360⁻¹ ⋅ (x + 59,5)) + 0,5
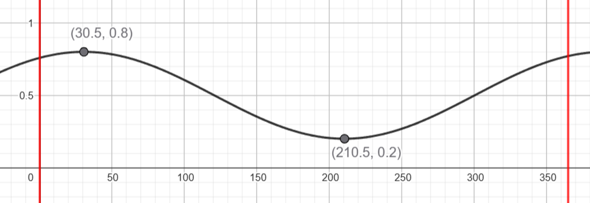
Hier ist der Verlauf einmal aufgezeichnet: