Sinus- und Kosinusfunktion - Lösungen im Intervall angeben?
Hallo Experte! Ich brauche deine Hilfe 💪
Hier ist ja in der Klammer von Sinus vor dem x noch „pi/3“. Deshalb muss ich die Periode „p = 2pi / k“ ausrechnen. Hierbei verstehe ich nicht das Ergebnis. Was kann ich mit dem Ergebnis anfangen (unter dem Aufgabenbild ist meine Rechnung)?
“Geben Sie alle exakten Lösungen im Intervall [0; 2pi] an.“

—> Berechnung der Periode:
p = 2pi / k
p = 2pi / (pi/3)
p = 6
Bei anderen Aufgaben kommt immer „p = Zahl pi“ raus. Also immer ein pi dahinter. Und eine Zeichnung von Sinus zum Beispiel geht immer bis 2pi bis der ganze „Kreis“ abgebildet ist.
(Beispiel andere Aufgabe, wo ich es verstehe:
Intervall [0; 2pi]
cos(x/2) = 0,5
—> Berechnung der Periode:
p = 2pi / k
p = 2pi / (1/2)
p = 4pi
)
Was fange ich also mit dem Ergebnis der Periode bei meiner Aufgabe von „p = 6“ an?
Meine Rechnung (falsch, x1 müsste 3,5 sein):

2 Antworten
Das ist schon richtig. In der Periode muss nicht unbedingt pi auftauchen. So könnte z.B. eine Schwingung eine Periode von 6 s haben und wenn man die Zeit t auf der x-Achse aufträgt, ist der Nulldurchgang bei 3 und bei 6 Sekunden.
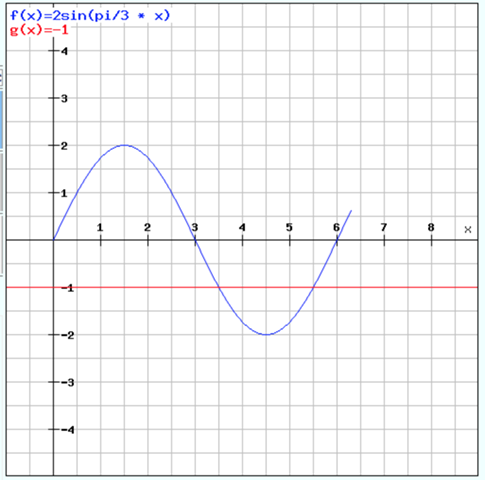
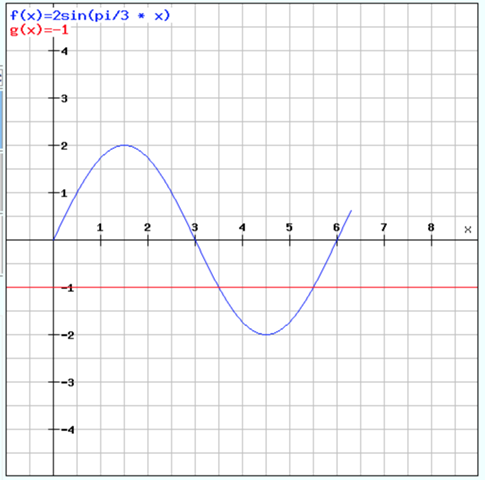
Zeichnerisch sieht die Lösung dann so aus:
f(x) ist die linke Seite der Gleichung und g(x) ist die rechte Seite der Glleichung. Wo beide Funktionen gleich sind, sich also schneiden, liegen die Lösungen für x. Das wären laut Graph offensichtlich x1 = 3,5 und x2 = 5,5.
Der Fehler liegt im Ansatz bzw. in fehlendem Wissen zur Umkehrfunktion des Sinus.
Die Umkehrfunktion des sinus ist der arcussinus. Der wird häufig auch anders geschrieben, wobei mögliche Schreibweisen sind:
arcussinus, arcsin, asin, sin^-1
Taschenrechner geben dafür immer nur eine Lösung aus und zwar die, die im Intervall [-π/2; π/2] liegt. Das sind aber nicht alle Lösungen. Die weiteren Lösungen muss man selber errechnen.
Wenn man die Gleichung nach x auflöst, kommt raus:
x = 3/π * sin^-1(-0,5)
Dafür wirft der Taschenrechner aus:
x1 = -0,5
Um die zweite Lösung innerhalb einer ganzen Schwingung unabhängig vom Intervalll zu rechnen, ergibt sich aus der Symmetrie der Sinusfunktion:
x2 = p/2 - x1 = 3 -(-0,5) = 3,5
Nun müssen wir überprüfen, ob x1 und x2 schon im gesuchten Intervall [0; 2π] liegt.
Das ist für x2 = 3,5 der Fall. Da müssen wir nicht weiter rechnen.
x1 liegt aber außerhalb des gegebenen Intervalls. Um die periodische Wiederholung dieser Lösung zu ermitteln wenden wir die Formel an:
xi = x1 ± n*p mit n ∈ ℕ
Wir müssen also natürliche Vielfache der Periode abziehen oder addieren, um die Wiederholungslösungen zu finden.
Es lässt sich abschätzen, dass wir von -05 mit der Addition einer Periode ins Intervall [0; 2π] kommen.
Also rechnen wir:
x3 = x1 + 6 = -0,5 + 6 = 5,5
Damit haben wir die beiden Lösungen gefunden (neue Nummerierung von x):
x1 = 3,5
x2 = 5,5
Die Gleichung allererst nach x aufzulösen habe ich gerade auf Papier gemacht und verstanden. Nur verstehe ich nicht warum meine Lösung falsch ist. Ich habe ja die Substitution angewendet. Und den Schritt mit * 3/pi erst später bei der Rücksubstitution gemacht.
Bei anderen Aufgaben hatte ich bei der Substitution keine Fehler. Wo liegt hier genau mein Fehler?
Ahh - immer wenn wir die Zahl vor dem x in der Sinus bzw. Kosinusfunktion durch z substituieren, rechnen wir z1 aus, indem wir mit der normalen Periode von p = 2pi (denn die andere haben wir ja rausgenommen und nehmen sie erst wieder bei der Rücksubstitution. Wir können also nicht rausnehmen, und trotzdem mit der Periode rechnen, die wir ja erst beim Ende beim Rücksubstituieren wieder nehmen) rechnen. Beim Rücksubstituieren fügt man dann wieder den Wert für z ein.
Habe es richtig rausbekommen, das muss ich mir nun gut einprägen!💪
Habe es richtig rausbekommen, das muss ich mir nun gut einprägen!
Das ist das Wichtigste. Mein Rechenweg war ja etwas anders, also ohne Substitution. Aber wenn das klappt und zum richtigen Ergebnis führt, ist das voll in Ordnung.
Kannst du mir bei der Frage ein bisschen weiterhelfen (dort ist noch Aufgabe 3 in der Frage; andere Aufgaben habe ich dort in der Frage entfernt)
https://www.gutefrage.net/frage/mathe-trigonometrische-funktionen---wiedereinstiegshilfe
Hier verstehe ich nicht wie ich genau den Winkel zeichnerisch bestimme. Jemand schrieb mir dort, bei 0,5 eine waagerechte Linie zeichnen, verstehe aber nicht wie genau und wie ich dann die 30 Grad ablesen kann.
Vielen Dank für deine Hilfe und deine Zeit, die du hier investiert um mir und anderen täglich weiterzuhelfen. 💚
Kannst du mir bei dieser Frage ein wenig weiterhelfen? 👍😬💚
https://www.gutefrage.net/frage/dringende-hilfe-benoetigt---exponentialfunktionen
Wurden deine Fragen inzwischen befriedigend beantwortet?
Ich habe es leider noch nicht so wirklich verstanden. Zu 100% verstanden davon habe ich die zusätzliche Frage, die nichts mit den Fragen in oberen Teil zu tun hatte, und weiß nun, dass 0 <gleich x <gleich 2pi das selbe bedeutet wie „Intervall [0; 2pi].
2·sin(𝜋/3 · x) = -1 → sin(𝜋/3 · x) = -½ → (𝜋/3 · x) = arcsin(-½) → x ausrechnen und schauen, welche der Lösungen im Intervall ist (Achtung: für arcsin(-½) erhältst du 2 Lösungen!)
Ich verstehe von dem geschrieben irgendwie so gut wie garnichts… Was bedeutet hier dieses arcsin?
Hatten das noch nicht in der Schule. Gibt es da eine andere Methode zum lösen dieser Aufgabe? Wenn nicht, dann gerne arcsin erklären und wie/wo man es mit dem Taschenrechner dann ausrechnet.
"arcsin" heißt Arcussinus und ist die Umkehrfunktion des Sinus. Er gibt dir also an, bei welchem Winkel (Grad oder Bogenmaß; hier: Bogenmaß!) der Sinuswert -0,5 ist.
Am TR steht meistens "sin⁻¹". (Bogenmaß einstellen! → "RAD", nicht "DEG")
Das mit von DEG zu RAD wechseln ist mir bewusst. sin^(-1) ist mir ebenfalls bewusst. Jetzt weiß ich, dass ich es auch arcsin/Arcussinus nennen könnte, vielen Dank!
Ich habe die Frage mit meiner Rechnung ergänzt. Kannst du nachschauen wo ich einen Fehler gemacht habe? 🤔
Ich habe die Frage mit meiner Rechnung ergänzt. Kannst du nachschauen wo ich einen Fehler gemacht habe? 🤔