Hilfe in Mathe Aufgabe?
bestimme jeweils grafisch oder numerisch alle lösungen der gleichung sin (x) = 0,7 im gegebenen intervall.
(1) A= 0;pi
(2) B = 0;2pi
(3) C = -pi; pi
(4) D= 3pi; 4pi
(1) sin(x)=0,7 <=> x=arcsin(0,7)
(arcsin=sin^(-1), gesprochen "Arkussinus)
1. Lösung:
x_1=arcsin(0,7)≈0,755
0<0,755<π passt also.
2. Lösung:
Da y>0 die obere Formel anwenden:
x_2=π–arcsin(0,7)≈2,36
0<2,36<π passt also auch
Und was willst du jetzt wissen?
wie man (2) B = 0;2pi
(3) C = -pi; pi
(4) D= 3pi; 4pi , berechnet
Ich erstelle eben ein Verfahren, das sich auf alle Aufgaben anwenden lässt. Kann ein paar Minuten dauern.
okeee:)
2 Antworten
B) ist identisch mit A), weil im Intervall von pi bis 2pi der Sinus negativ ist.
C) ist identisch mit a, da im Bereich -pi bis 0 der Sinus negativ ist.
D) hat Lösungmenege leer, da im Intervall 3 pi bis 4 pi der Sinus negativ ist.
Das ist logisch bestimmt. Rechnerisch müsstest du so vorgehen. Zu deinen beiden Werten aus A) jeweils immer 2 \pi dazuzählen bzw. 2 \pi abziehen. Und da wirst du feststellen, dass du dabei aus den genannten Grenzen komplett rausfällst (Aufgabe D) oder nur aus einem Teil (B) und C).
Du musst nur diese Formel anwenden können:
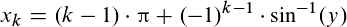
Für die erste Lösung setzt du für k=1 ein, für die zweite k=2 und so weiter...
Das machst Du so lange, bis Du nicht mehr im angegebenen Intervall bist. Wenn Du im negativen bist, zählen die Ergebnisse erst, wenn Du im positiven bist (in dieser Aufgabe nicht der Fall). y ist bei Deiner Aufgabe 0,7.
_________________________________________________
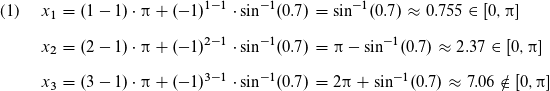
Es gibt nur zwei Lösungen, die im Intervall A=[0,π] liegen, nämlich x_1 und x_2. Das Ergebnis x_3 ist größer als π, deswegen zählt es nicht mehr.
[0,π] bedeutet, dass für x gilt: 0 ≤ x ≤ π
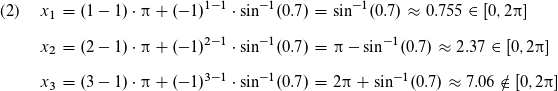
Hier erhalten wir tatsächlich die selbe Lösungsmenge, da x_3 immernoch größer als die rechte Intervallgrenze (2π) ist.
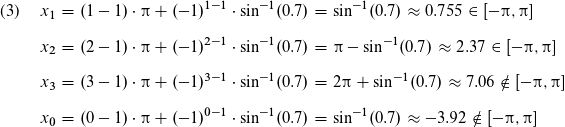
Schon wieder haben wir nur x_1 und x_2 als Lösungen, da x_3 wieder zu groß ist, aber x_0 zu klein ist.
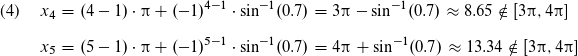
Hier gibt es gar keine Lösungen, da x_4 zu klein, aber x_5 zu groß ist.
Ich hoffe, ich konnte helfen :)
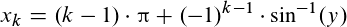
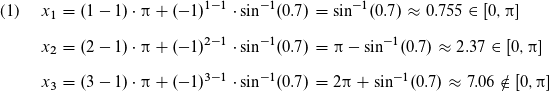
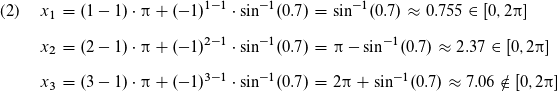
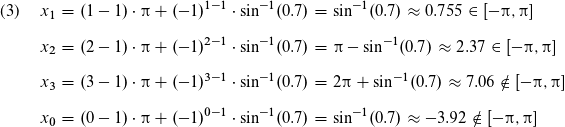
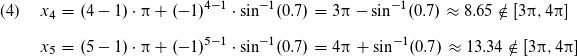
Doch, doch! Soory... was sag ich da. Ja, bei A,B,C ist das gleiche
ne es muss a,b,d sein....c nicht weil c minus ist
also: (0,7 - 1) mal pi plus (-1) hoch 0,7 -1 mal arcsin von 0,7??
und ds ist jetzt grafisch oder numerisch bestimmt