Wie rechnet man diese Aufgabe?

Gib alle Winkel im Intervall [0; 2pi] im Bogenmaß mit der Eigenschaft sina=cos a an. Begründe dies.

Answer 1

[indiachinacook]

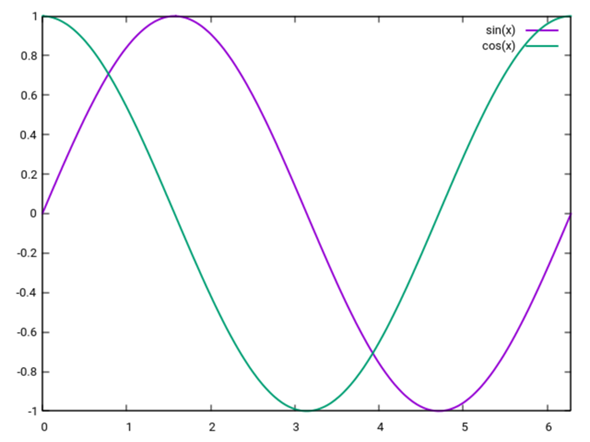
Es kann nur zwei geben, nämlich π/4 und 5π/4, mit den Werten ±√2/2 Das sieht man z.B. an den Funktions­graphen:

Aber man kann es sich natürlich auch leicht ausrechnen, indem man die Gleichung aufschreibt und dann durch den Cosinus dividiert:

sin(x) = cos(x)

sin(x)/cos(x) = tan(x) = 1

Und wer den inversen Tangens mit all seinen Tücken beherrscht, kommt sofort zum Resultat.

Answer 2

[Tannibi]

Begründen kannst du es mit dem Einheitskreis.
Der cos ist der x- und der sin der y-Wert; darum ist
sin = cos auf der Winkelhalbierenden des 1. und 3.
Quadranten. Das sind 45° und 225° bzw. hier
pi/4 und 5*pi/4.

Comments

[TomatePflaume]

Ah danke dir. Jetzt merk ich die Aufgabe ist richtig leicht, ich hab nur zu kompliziert gedacht