Mathe (Additionstheoreme) - wie löst man diese Gleichung?
Kann mir jemand bei der a) weiterhelfen?
Aufgaben:

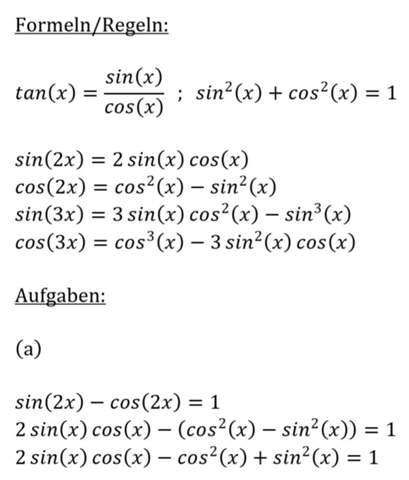
2sin(x) cos(x)
wieder durch sin(2x) zu ersetzen, denke aber nicht, dass es sonderlich viel bringt.
So, hab das jetzt erneut versucht: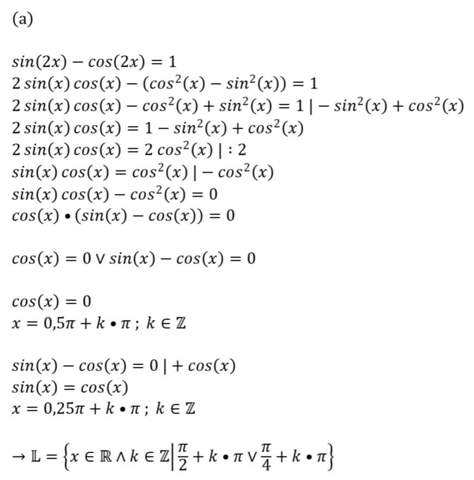
Passt das so?😊
3 Antworten
Doch es sollte passen, wende zuerst die Regeln für Sin(2x) und cos(2x) an, und bringe alles von cos(2x) rüber. Du erhälst dann:
2sin(x)cos(x)=1-sin^2(x)+cos^2(x)
Nutze dann, dass 1-sin^2(x) = cos^(x) gilt und erhalte dann:
2sin(x)cos(x)=2cos^2(x)
Den Rest solltest du selbst schaffen.
Also verrechnet hab ich mich zwar nicht, aber vielleicht schreibt man ja hier die Lösungsmenge anders auf 😅
Hab's geschafft, danke dir 😊 Kannst du vielleicht kurz schauen, ob ich die Lösungsmenge korrekt aufgeschrieben hab?
Stimmt, ja. Die Nullstellen vom cos sind auch noch in der Lösungsmenge. Danke.
Sinus Quadrat plus Kosinus Quadrat = 1
Minus übersehen, sorry
Klammer doch mal Sinus^2 oder Kosinus^2 aus, das könnte funktionieren.
Der letzte Schritt ist meine Äquivalenzumformung, da cos(x) auch 0 sein kann, du verschluckst damit Lösungen.