Minimale Periode trigonometrischer Funktionen?

sin(x) hat die Periode 2PI

sin(2x) hat die Periode 2PI/2 = PI

cos(x) hat 2PI

cos(2x) hat PI

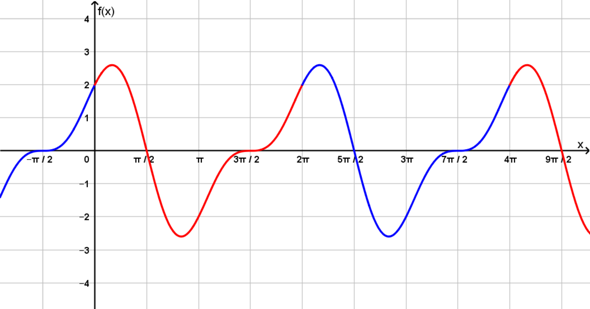
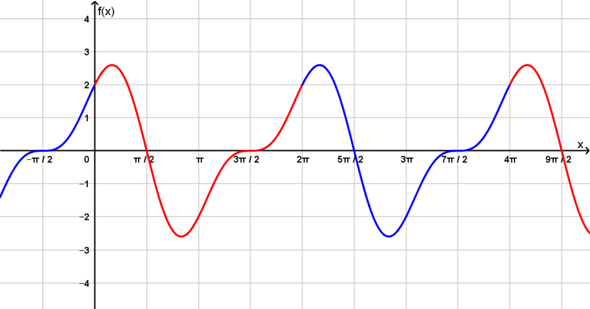
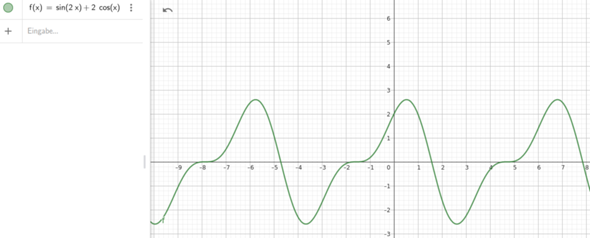
a) f(x) = sin(2x) + 2*cos(x)

=> Was ist hier die minimale Periode von f? PI oder 2PI?

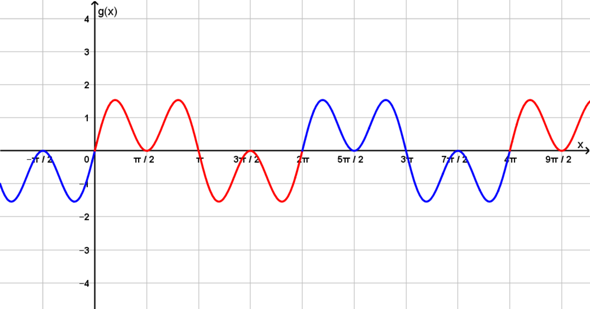
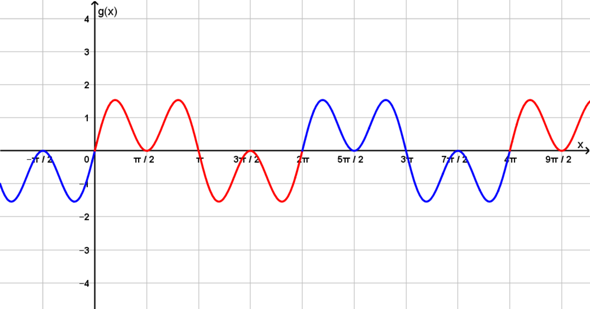
b) g(x) = sin(2x) * 2*cos(x)

=> Was ist hier die minimale Periode von g?

Answer 1

[mihisu]

a)

Wenn die Periode π wäre, so müsste insbesondere f(0) = f(π) sein. Nun ist jedoch...

$f(0)=\underbrace{\sin(\overbrace{2\cdot 0}^{=0})}_{=0}+2\cdot \underbrace{\cos(0)}_{=1}=0+2\cdot 1=2$

$f(\pi)=\underbrace{\sin(2\cdot \pi)}_{=0}+2\cdot \underbrace{\cos(\pi)}_{=-1}=0+2\cdot (-1)=-2$

$f(0)=2\ne -2=f(\pi)$

Demnach ist die Funktion nicht π-periodisch, sondern tatsächlich ist 2π die minimale Periode der Funktion f.

b)

Wenn die Periode π wäre, so müsste insbesondere g(π/6) = g(π/6 + π) sein. Nun ist jedoch...

$g(\frac{\pi}{6})=\underbrace{\sin(\overbrace{2\cdot \frac{\pi}{6}}^{=\frac{\pi}{3}})}_{=\frac{\sqrt{3}}{2}}\cdot 2\cdot\underbrace{\cos(\frac{\pi}{6})}_{=\frac{\sqrt{3}}{2}}=\frac{\sqrt{3}}{2}\cdot 2\cdot \frac{\sqrt{3}}{2}=\frac{1}{2}\cdot\left(\sqrt{3}\right)^2=\frac{1}{2}\cdot 3=\frac{3}{2}$

$g(\pi+\frac{\pi}{6})=g(\frac{7\pi}{6})=\underbrace{\sin(\overbrace{2\cdot \frac{7\pi}{6}}^{=\frac{7\pi}{3}})}_{=\cos(\frac{\pi}{3})=\frac{\sqrt{3}}{2}}\cdot 2\cdot\underbrace{\cos(\frac{7\pi}{6})}_{=-\frac{\sqrt{3}}{2}}=\frac{\sqrt{3}}{2}\cdot 2\cdot \left(-\frac{\sqrt{3}}{2}\right)=-\frac{3}{2}$

$g(\frac{\pi}{6})=\frac{3}{2}\ne -\frac{3}{2}=g(\pi+\frac{\pi}{6})$

Demnach ist die Funktion nicht π-periodisch, sondern tatsächlich ist 2π die minimale Periode der Funktion g.

Comments

[mihisu]

Wenn sich die Funktionen nicht zufällig passend gegenseitig ergänzen/aufheben, so ist die neue minimale Periode das kleinste gemeinsame Vielfache (kgV) der vorigen minimalen Perioden.

Im konkreten Fall:

kgV(π, 2π) = kgV(1 ⋅ π, 2 ⋅ π) = kgV(1, 2) ⋅ π = 2 ⋅ π =  2π

Aber wie bereits geschrieben: Es könnte auch sein, dass die Einzelfunktionen sich entsprechend gegenseitig ergänzen/aufheben, dass die minimale Periode dennoch kleiner ist. [Was hier aber nicht der Fall ist.] Das ist aber im Allgemeinen nicht unbedingt leicht zu prüfen. Wie man das am einfachsten nachweisen kann, hängt oftmals stark von der gegeben Funktion ab.

Answer 2

[MichaelH77]

die beiden Funktionen überlagern sich. Die Periode der zusammengesetzten Funktion ist gleich der größeren der beiden

schau dir das Schaubild an, hier kann man es gut erkennen, dass die Periode 2pi (ungefähr 6.28) ist

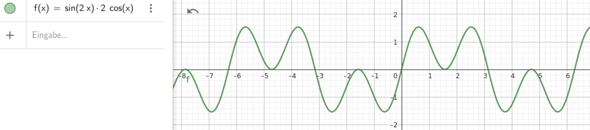
bei der Multiplikation der beiden Funktionen:

Comments

[RedDevil1982]

Und bei g(x) = sin(2x) * 2*cos(x)?

[MichaelH77]

@RedDevil1982

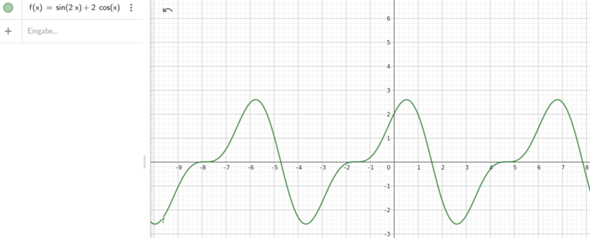
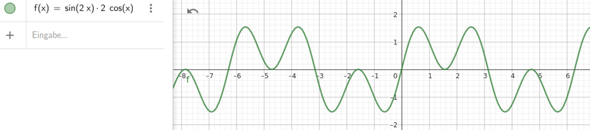
das gleiche, aber anderer Funktionsverlauf. Ich füge gleich das Bild der obigen Antwort hinzu