Sinusfunktion aufgabe?

Kann mir irgendeiner diese Aufgabe erklären? Die kommt morgen bei mir in der Schulaufgabe dran und ich checke es nicht. Liebe Grüße
2 Antworten
Du willst also eine Funktion bauen, die Schwankungen der Temperatur um einen Mittelwert angibt, und sie soll eine Periode von 24 Stunden haben (also nur von der Tageszeit abhängen, aber für jeden Tag dieselben Werte geben).
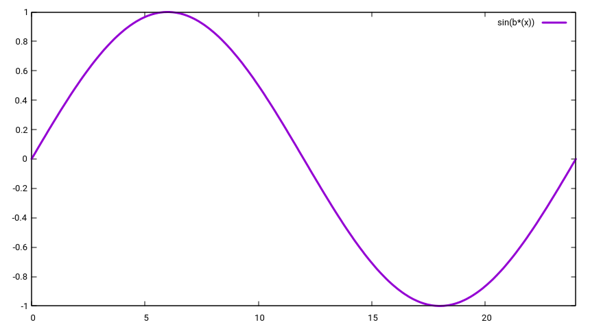
Wenn ich eine solche Funktion konstruieren will, dann denke ich mir zunächst mal eine Sinusfunktion sin(bt) aus, die genau 24 Stunden Periode hat. Nach 24 Stunden muß bt also genau den Wert b⋅24=2π haben, weil der Sinus mit 2π periodisch ist. Wir bekommen also b=π/12 heraus, und die Funktion sieht so aus:

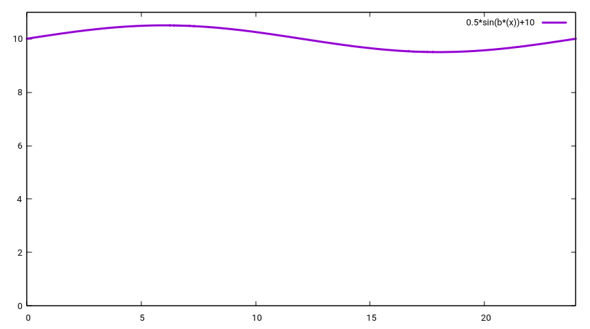
Du siehst sofort, daß der Mittelwert 0 ist (das können wir korrigieren, indem wir noch ein d dazuaddieren), und die Schwankungsbreite ist ±1 (das können wir korrigieren, indem wir noch ein a draufmultiplizieren), z.B. d=10 und a=½ läßt die Temperatur um ein halbes Grad rund um 10 °C schwanken:

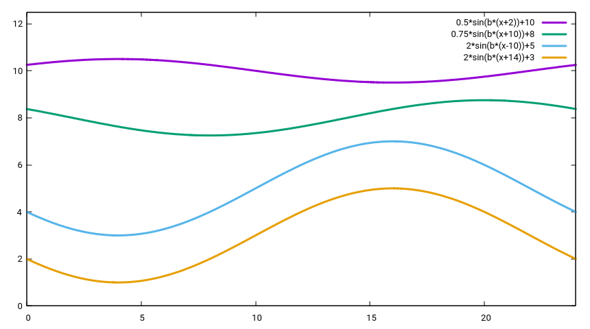
Das letzte, was wir noch hinkriegen müssen, ist die zeitlich Lage der Minimaltemperatur und der Maximaltemperatur zu verschieben; der Sinus hat ja immer die Maximaltemperatur bei 6 Uhr (ein Viertel des Tages) und die minimale um 18 Uhr (drei Viertel). Dazu ist der Parameter c in Deiner Formel gut, der verschiebt die Extremwerte nach links:

Du siehst in diesen Beispielen auch, daß b=−10 (blau) und b=14 (orange) dieselbe Lage der Maxima hat, weil es je egal ist, ob Du 10 Stunden vorgehst oder 14 Stunden zurück, Du kommst immer bei derselben Uhrzeit an.
Wir haben also gesehen, daß b=π/12 immer denselben Wert haben muß, aber die anderen Parameter müssen jeweils an die Viecher angepaßt werden.
- Der Parameter d ist der durchschnittliche Wert der Körpertemperatur. Gegeben sind Maximum und Minimum, also bestimmen wir d als den Mittelwert der beiden angegeben Temperaturen. Für den Menschen sind das d=37 °C, für den Elefanten 36.3 °C und für die Eule 40.45 °C.
- a ist die Fluktuation, also Maximalwert minus Durchschnitt. Das sind für die drei Tierarten 0.5 K, 0.6 K und 0.65 K.
- Die Maxima werden um 16, 18 und 2 Uhr erreicht, das ist −10, −12 und 4 Stunden vor 6 Uhr, das sind die Werte c, um die die Kurve zu verschieben ist.
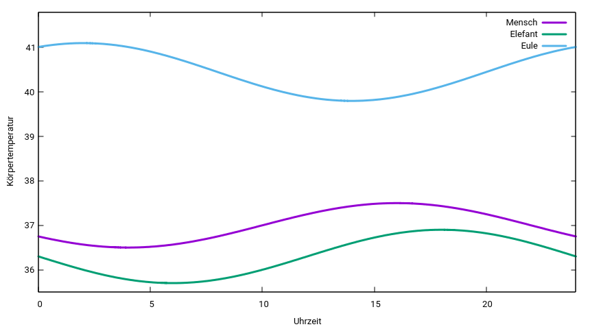
Und so sehen die Kurven dann aus:

Man sieht sehr deutlich, wer tagaktiv ist und wer nachtaktiv.
plot [0:24] [35.5:41.8] 0.5*sin(pi/12*(x-10))+37 lw 3 title "Mensch", 0.6*sin(pi/12*(x-12))+36.3 lw 3 title "Elefant", 0.65*sin(pi/12*(x+4))+40.45 lw 3 title "Eule"
Das habe ich ja weiter oben ausgeführt: Von Natur aus hat der Sinus sin(π/12t) bei 6 Uhr sein Maximum (90° bzw. ein Viertel der Periode), wir bohren das daher zur Form sin(π/12(t+c)) auf. Wenn c=1, dann erreicht der Sinus das Maximum bereits eine Stunde früher, bei c=2 zwei Stunden früher etc. Die Eule will ihr Maximum bei 2 Uhr haben, das ist vier Stunden vor 6 Uhr, also c=4.
Der Mensch will aber die Maximale Körpertemperatur um 16 Uhr erreicht, das ist 10 Stunden später und daher −10 Stunden früher. Alternativ könntest du auch sagen, daß es von 16 Uhr 8+6=14 Stunden bis nach 6 Uhr des nächsten Tages sind, also kannst Du für c sowohl den Wert −10 als auch +14 verwenden.
Ich komme gerade so mit aber wieso ist bei 6 Uhr gleich nochmal der Höhepunkt. Es tut mir wirklich leid aber in Mathe stelle ich mich zu blöd an
Der Sinus sin(x) hat bei x=0 den Wert Null, bei x=π/2 sein Maximum +1, bei x=π wieder den Wert Null und bei 3π/2 das Minumum; ab 2π wiederholt er sich ja.
Also liegt das Maximum ein Viertel in die Periode. Wir haben die Periode statt von 0 bis 2π auf 0 bis 24 h umskaliert (mit b=π/12), aber natürlich hat der Sinus immer noch bei einem Viertel der Periode das Maximum; ein Viertel von 24 ist aber 6 Uhr. Um das zu verändern, muß man etwas dazuaddieren oder davon wegsubtrahieren.
Jetzt bin ich gerade am Busbahnhof von Marrakesh angekommen und muß eine gute Stunde richtung Stadtzentrum laufen, um ein Hotel zu finden. So schnell kann ich also nicht mehr antworten, versuch es lieber alleine zu verstehen.
Du bist eine Legende für mich,vielen Dank. Eigentlich sollte ich morgen auf die klausur schreiben dass ich es nur dank dir verstanden habe. Vielen vielen Dank für deine Geduld und Hilfe.
Zeichne Dir doch den Temperaturverlauf ungefähr mal auf.
Du kennst das Maximum und das Minimum - und damit auch den Mittelwert, um den die Sinuskurve schwankt. Damit doch auch "d" schon bekannt, oder?
Da Du weißt, dass der Sinus selber (ohne Vorfaktor) nur zwischen +1 und -1 schwankt, kann man doch auch etwas aussagen über den faktor "a".
Und die Zeitangaben bestimmen dann den Rest, der unter der Sinusfunktion steht und die Periodendauer beinhaltet, die ja praktisch auch bekannt ist (durch die Zeitangaben).
Eigentlich ist nur logisches Denken gefragt.
Vielen vielen Dank, aber ich verstehe das mit dem c noch nicht ganz. Wieso kommst du auf -10 -12 und 4 Stunden vor 6? Wieso ist 6 so wichtig?