Ich hab das so gerechnet, wie bekomm ich jetzt t heraus?

3 Antworten
L(t) = 12 + 6.24 * sin(1/6*π*t)
Die Tageslänge ändert sich am schnellsten, wenn die Ableitung von L(t) einen Extrempunkt aufweist.
L'(t) = 26/25 * π * cos(1/6*π*t)
Extrempunkte von L'(t) suchen:
L''(t) = -26/150 * π² * sin(1/6*π*t)
L''(t) = 0 ?
-26/150 * π² * sin(1/6*π*t) = 0
für t = 3 und t = 6, also ca. am 21.Juni und ca. am 21.Sep (die einzelnen Monate sind nicht gleich lang).
Tageslängen zu diesen Zeitpunkten:
L(3) = 456/25 = 18.24 Stunden
L(6) = 12 Stunden
So sieht der Graph aus:

Was die Änderungsrate betrifft, gilt für alle Funktionen (nicht nur trigonometrische) folgendes:
geringste Änderung: Hoch- und Tiefpunkte. Da geht die Änderung gegen 0.
Berechnung: 1. Ableitung zu 0 setzen.
Stärkste Änderung: Wendepunkte
Berechnung: 2. Ableitung zu 0 setzen.
(1) Ableiten der Funktion (hast du richtig):
L'(t) = 26/25 * π * cos(π/6 * t)
L''(t) = - 13/75 * π^2 * sin(π/6 * t)
(2) 2. Ableitung zu 0 setzen, um Wendepunkt zu finden:
L''(t) = 0
sin(π/6 * t) = 0
t1 = 0
π/6 * t2 = π
t2 = 6
Ergebnis: Die Tageslänge ändert sich am schnellsten am 21. März (Frühlingsbeginn) und am 21. September (Herbstbeginn).
(3) Tageslänge:
L(0) = 12 + 6,24 * sin(pi/6 * 0) = 12 + 0 = 12 h
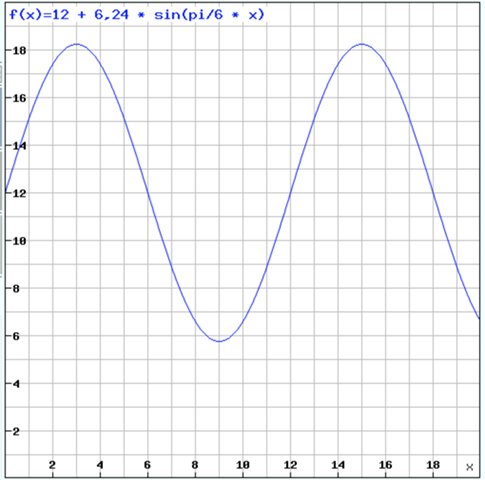
Wenn die "stärkste Änderung" einer Funktion gesucht wird, geht es um die Wendepunkte, also muss die zweite Ableitung gleich Null gesetzt werden. Das führt hier zu t = 6 * n ; n ϵ Z. Der Beginn ist der 21. März.
n = 0: 21. März
n = 1: 21. September
Tageslänge an diesen Tagen jeweils 12 Stunden