Hilfe bei Matheaufgabe?
Ich sitze an dieser Aufgabe jetzt schon 1 Stunde und ich verstehe nicht, wie ich Aufgabe B berechnen. Ich habe keine Ahnung.
Auf einem Berg steht ein 10 m hoher Turm. Von einem Punkt im Tal aus sieht man den Fußpunkt des Turmes unter dem Winkel α = 44,3 ° und die Spitze des Turmes unter dem Winkel β = 45,5 °. a) Fertige eine Skizze an, in der du alle gegebenen Größen einträgst. b) Berechne die Höhe des Berges über der Talsohle.
4 Antworten
h = Höhe über der Talsohle
d = (horizontale) Entfernung vom Blickpunkt bis zum Lot unter dem Turm
h/d = tan(α)
(h+10)/d = tan(β)
--> (h+10)/h = tan(β) / tan(α)
Löse nach h auf.
Aufgabe
e = ht / ( TAN(β) - TAN(α) )
e = 10 / ( TAN(45,5) - TAN(44,3) )
e = 239,5309 m
---
hB = e * TAN(alpha)
hB = 239,5309 * TAN(44,3)
hB = 233,748414 m
Höhe des Berges ist 233,748 m

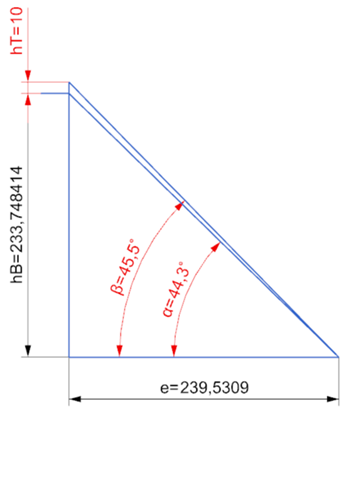
Es sei Alpha=a und Beta=b sowie h die Höhe des Berges und x die Entfernung des Berges bis zur gedachten Bergmitte auf der Talsohle. Dann ist
(1) tan(a)= h/x
(2) tan(b)=(h+10)/x
Aus (1) folgt x=h/tan(a)
Eingesetzt und h aufgelöst ergibt sich
h=10×tan*a/(tan(b)-tan(a))
Die Winkel für a und b eingesetzt ergibt
h~233,75 m
Ist doch easy überleg dir einen Maßstab zeichne die Winkel vom fußpunkt des Turmes und mess das ganze aus und Rechne es um
Ich meinte die 10m von der Bergspitze im Maßstab messen und zeichnen sorry falls das unklar war habe ja nochmal eine ausführliche Beschreibung gegeben
Zeichne eine horizontale Linie für die Talsohle und eine schräge Linie für den Berg. Auf dieser Linie zeichnest du einen senkrechten Turm mit einer Höhe von 10 m. Markiere einen Punkt im Tal (P) und zeichne zwei Linien von Punkt P: eine zum Fuß des Turmes (Winkel α = 44,3°) und eine zur Spitze des Turmes (Winkel β = 45,5°). Beschrifte alle Punkte und Winkel.
Um die Höhe des Berges zu berechnen, nenne die Höhe des Berges h_B und die horizontale Entfernung zwischen P und dem Fuß des Turmes d. Mit dem Winkel α gilt: h_B = d * tan(α), und mit dem Winkel β gilt: h_B + 10 = d * tan(β).
Ziehe die erste Gleichung von der zweiten ab, um d zu berechnen:
10 = d * (tan(β) - tan(α)),
d = 10 / (tan(β) - tan(α)).
Setze die Werte für tan(α) und tan(β) ein:
tan(44,3°) ≈ 0,972 und tan(45,5°) ≈ 1,016.
d = 10 / (1,016 - 0,972) = 10 / 0,044 ≈ 227,27 m.
Berechne dann die Höhe des Berges:
h_B = d * tan(α),
h_B = 227,27 * 0,972 ≈ 220,81 m.
Die Höhe des Berges über der Talsohle beträgt ca. 220,8 m.
Und ich bin in der 8. Klasse also so schwer ist es auch wieder nicht
Hier sind gerechnet und nicht gemessen werden.