Physik - Wie berechnet man den richtigen Winkel, um eine Strömung zu kompensieren?

Angenommen, eine Schwimmerin möchte einen 380 m breiten Fluss überqueren, der mit 1,3 m/s parallel zum Ufer strömt. Sie kann mit 1,7 m/s schwimmen (relativ zum Wasser) und will genau auf der gegenüberliegenden Seite ankommen, ohne abgetrieben zu werden.

Unter welchem Winkel zur Strömung muss sie schwimmen, damit sie gerade rüberkommt?

Wie würde das als rechtwinkliges Dreieck aussehen, und wie kann man das zeichnerisch lösen? Eine kleine Skizze mit beschrifteten Seiten würde sehr helfen…

Danke!

Answer 1

[mihisu]

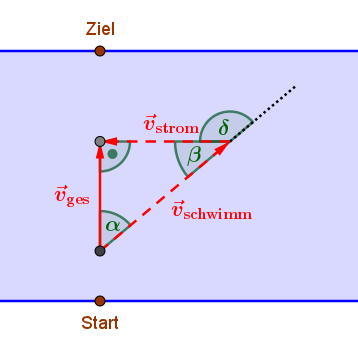
Eine dazu passende Skizze könnte beispielsweise so aussehen...

Die Strömungsgeschwindigkeit und die Schwimmgeschwindigkeit ergeben zusammen (geometrisch addiert, also die entsprechenden Pfeile aneinandergesetzt) eine resultierende Gesamtgeschwindigkeit, die im rechten Winkel zum Ufer bzw. im rechten Winkel zur Strömungsgeschwindigkeit verlaufen soll.

Gesucht ist der Winkel δ. Gegeben sind die Geschwindigkeitsbeträge v[schwimm] = 1,7 m/s und v[strom] = 1,3 m/s. (Außerdem ist die Breite des Flusses gegeben, die hier aber nicht relevant ist.)

Nun kann man in einer maßstabsgetreuen Skizze den entsprechenden Winkel messen, um das zeichnerisch zu lösen. (Meine Skizze ist übrigens maßstabsgetreu gezeichnet.) Oder man könnte mit etwas einfacher Trigonometrie einen passenden Innenwinkel im Geschwindigkeitsdreieck berechnen, und damit dann den gesuchten Winkel δ erhalten.

====== Ergänzung ======

Möglicher Rechenweg zum Vergleich...

$\cos(\beta)=\frac{v_\text{strom}}{v_\text{schwimm}}$

$\rightarrow\quad \beta=\cos^{-1}\left(\frac{v_\text{strom}}{v_\text{schwimm}}\right)=\cos^{-1}\left(\frac{1\text{,}3\,\frac{\text{m}}{\text{s}}}{1\text{,}7\,\frac{\text{m}}{\text{s}}}\right)\approx 40\text{,}1\degree$

$\delta + \beta = 180\degree$

$\rightarrow\quad \delta =180\degree-\beta\approx 180\degree -40\text{,}1\degree = 139\text{,}9\degree$

====== Ergänzung (Klärung des Winkels, siehe Kommentare) ======

Comments

[User2828p]

Vielen Dank für die ausführliche Antwort!
Aber den Winkel den der Schwimmer schwimmen müsste, um gerade rüber zu kommen wäre doch B oder?
Also diesen müsste ich doch ablesen oder?

[mihisu]

@User2828p

Gefragt ist...

„Unter welchem Winkel zur Strömung muss sie schwimmen, damit sie gerade rüberkommt?“

Gesucht ist also der Winkel zwischen Schwimmrichtung und Strömungsrichtung.

Der Winkel β wäre zwar gewissermaßen auch ein Winkel zwischen den eingezeichneten Schwimm- und Strömungs-Geschwindigkeiten. ABER... Genau genommen ist dass nicht der Winkel im Bezug zur Schwimmrichtung. Sondern es wäre der Winkel im Bezug zur entgegengesetzten Richtung zur Schwimmrichtung. Denn der Geschwindigkeitspfeil der Schwimmgeschwindigkeit zeigt ja nicht vom entsprechenden Punkt weg, sondern vom entsprechenden Punkt weg. Die Schwimmrichtung ist ja hier in der Skizze nach oben-rechts, nicht nach links-unten.

Neben der Strömungsrichtung (nach links in der Skizze) ist hier für den richtigen Winkel also die Richtung in Schwimmrichtung (nach oben-rechts, in Verlängerung des Geschwindigkeitspfeils) relevant, nicht die entgegengesetzte Richtung (nach links-unten, entgegen der Schwimmrichtung).

Dementsprechend ist der Winkel δ genau genommen der richtige Winkel, der gesucht ist.

[CrazyChicken334]

@mihisu

Was müsste gegeben sein, damit Winkel alpha gesucht wäre?

[mihisu]

@CrazyChicken334

Besipielsweise könnte man dafür nach dem Winkel zwischen der tatsächlichen (resultierenden) Bewegungsrichtung einerseits und der Schwimmrichtung (Richtung der „Schwimmanstrengung“) andererseits fragen, wenn man den Winkel α suchen möchte.

[mihisu]

@User2828p

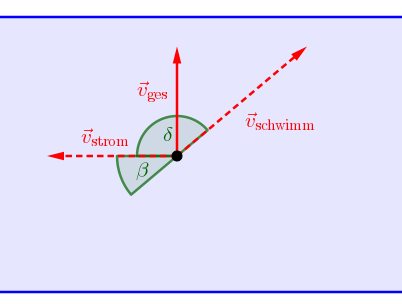
Ich habe übrigens nochmal am Ende meiner Antwort eine Skizze ergänzt, wie die Richtungen von einem Punkt ausgehend aussehen.

Würdest du auch hier auf die Idee kommen, dass der Winkel β gesucht wäre? Oder würdest du mir doch eher zustimmen, dass der Winkel δ der gesuchte Winkel zwischen Schwimmrichtung und Strömungsrichtung ist?

[CrazyChicken334]

@mihisu

Danke!

Answer 2

[ChrisGE1267]

Es muss lediglich gelten:

$\vec{v}_{eff} = \vec{v}_{Wasser} + \vec{v}_{Schwimmerin}$

Den Winkel kannst Du selbst ausrechnen. Er ist übrigens nicht von der Flussbreite abhängig…😀

Woher ich das weiß: Studium / Ausbildung – Kosmologie, ART und Stringtheorien

Answer 3

[electrician]

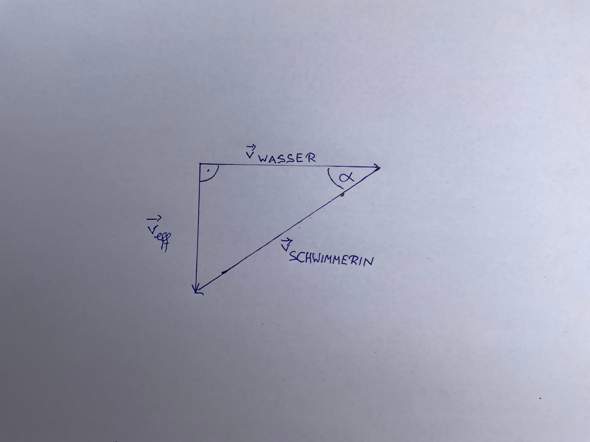
Sie muss 1,70 m diagonal schwimmen, während das Wasser sie 1,30 m mitreißt.

Damit hast Du eine Hypothenuse von 1,70 m und eine Gegenkathete von 1,30 m. Somit schafft sie pro Sekunde eine Entfernung vom Ufer von $AK\ =\ \sqrt{H^2-GK^2}=\sqrt{\left(1,70\ m\right)^2-\left(1,30\ m\right)^2}=1,0954\ m$

Den Winkel kannst Du mit dem Sinus bstimmen:
$α\ =\sin^{-1}\ \left(\frac{GK}{H}\right)=\sin^{-1}\ \left(\frac{1,30\ m}{1,70\ m}\right)=49,88°$

Answer 4

[segler1968]

Wieso machst Du dann nicht die Skizze? Gerade Linie über den Fluss. Rechtwinklig dazu eine Linie entgegen der Strömungsrichtung. Und dann den Anfang der ersten Linie mit dem der zweiten verbinden. Die Hypotenuse ist die Linie, die sie schwimmen muss. Die Strömung sorgt dann dafür, dass sie genau gegenüber ankommt.

Übrigens ist die Breite des Flusses egal.

Woher ich das weiß: Studium / Ausbildung – Physikstudium

Comments

[User2828p]

Wäre dann die Hypotenuse die Geschwindigkeit der Schwimmerin oder die andere Linie über den Fluss?

[Willy1729]

@User2828p

Hypotenuse ist 1,7, Gegenkathete 1,3.

Winkel ist Arkussinus (1,3/1,7). Rechner auf DEG einstellen!

[CrazyChicken334]

@Willy1729

Ist die resultierende Geschwindigkeit 1.095 m/s?

[Willy1729]

@CrazyChicken334

Ja, genau.