Mathe Hilfe SEHR dringend?

Und zwar hätte ich eine Frage zur Aufgabe 2b).
woran erkennt man dass es eine Streckung mit dem Faktor 2 in x Richtung ist und nicht in y- Richtung? Wie zeigt sich eine Streckung in x-Richtung?
3 Antworten
Strecken in x-Richtung bedeutet, der Graph wird in die Breite gezogen. Das erkennt man z. B. an den anschließend weiter (in x-Richtung) auseinanderliegenden Extrempunkten. Dass der Graph nicht in y-Richtung gestreckt/gestaucht wurde erkennst Du daran, dass z. B. die Differenz zwischen zwei Extrempunkten in y-Richtung die gleiche geblieben ist. Oder schiebst Du in Gedanken den nach oben verschobenen Graphen wieder nach unten zurück, liegen die Extremwerte auf gleicher Höhe wie die des Ausgangsgraphen.
Das kann man oft nicht auf Anhieb (oder auch gar nicht) sehen bzw. es gibt mitunter auch verschiedene Lösungsmöglichkeiten (es macht ja z. B. auch einen Unterschied ob man zuerst verschiebt und dann streckt oder zuerst streckt und dann verschiebt).
Hast Du z. B. f(x)=x² und die transformierte Funktion g(x)=4x², so kann g entstanden sein, indem f in y-Richtung mit Faktor 4 gestreckt wurde (g(x)=4*f(x)=4*x²) oder mit Faktor 1/2 in x-Richtung gestaucht (g(x)=f(x/(1/2))=(2x)²=4x².
Ehrlich gesagt, hätte ich das so auch nicht ad-hoc gesehen. Daher Achtung: die Lösung sagt "an der y-Achse gespiegelt" und wer dauernd fälschlicherweise - so wie ich - an eine Spiegelung an der x-Achse denkt, findet die Lösung nicht. Vielleicht hilft das folgende Bild:

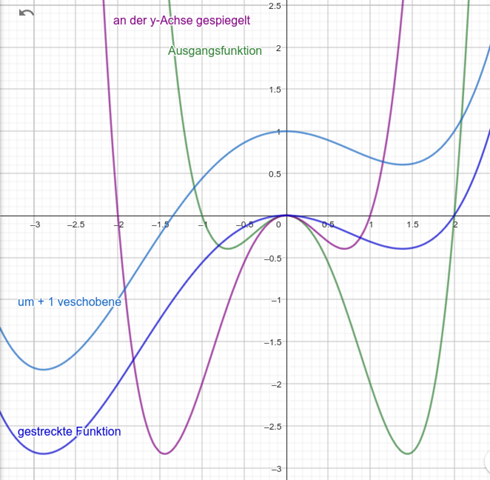
Ja das war tatsächlich auch mein Ansatz:) bloß hab ich mir jetzt die Frage gestellt wie es bei Parabeln oder Hyperbeln aussieht… Da kann ich ja schlecht irgendwelche Extrempunkte ablesen:( wie erkenn ich dann dass es (0,5x)^2 +4 ist und nicht einfach 0,5x^2 +4 .
Das sieht man ja optisch. Du kannst dir punkt raussuchen die übereinstimmen, zum beispiel die maximas und minimas bei y=1 und y=-1.75. Wenn die übereinstimmen hat es ja logischerweise keine y Dehnung
Ah, Du meinst die Differenz von hoch und Tiefpunkt ist bei beiden Funktionen gleich oder?
Aber was ist mit Parabeln oder Hyperbeln? Die haben ja keine Hochpunkte oder Tiefpunkte:(
Nicht die differenz, sondern du kannst ja direkt ablesen auf welcher y koordinate sie liegen. Da du ja eine verschiebung auf der Y achse hast, stimmen sie überein. Bei einer dehnung wäre das micht mehr der fall da sie in unterschiedliche richtungen verschoben werden würden
Ja das war tatsächlich auch mein Ansatz:) bloß hab ich mir jetzt die Frage gestellt wie es bei Parabeln oder Hyperbeln aussieht… Da kann ich ja schlecht irgendwelche Extrempunkte ablesen:( wie erkenn ich dann dass es (0,5x)^2 +4 ist und nicht einfach 0,5x^2 +4 .