Mathe?

Und zwar haben wir hier bei d) drei verschiedene Exponentialfunktionen. Den für g(x) war leicht zu bestimmen, da der y-Achsenabschitt erkennbar ist. Bei h(x) allerdings auch, also : 0,25× 2^x

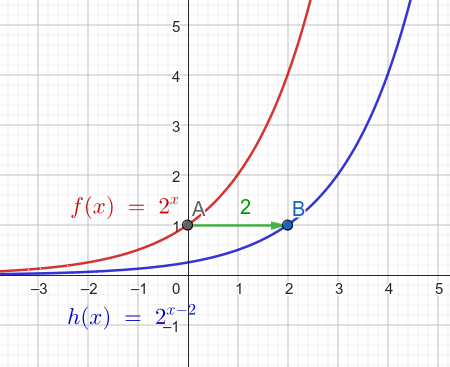
Mein Lehrer meint man könnte Parameter a auch so ausdrücken, dass man es für die Streckung in x Achse interpretieren könnte: 2^x-2

Wenn ich das überprüfe ist es ja richtig, aber wie kommt man darauf? Und meine zweite Frage ist, woran man am Graphen erkennt, dass der Graph in Bezug auf die Ursprungsfunktion gerade in y Richtung oder in x Richtung gestreckt wird?

Kann mir bitte jemande helfen

Answer 1

[verreisterNutzer]

dass man es für die Streckung in x Achse interpretieren könnte: 2^x-2

... für eine Streckung in x-Achse kann man es auf keinen Fall halten, sondern für eine Verschiebung um 2 Einheiten nach rechts und das ergibt sich aus den Rechenregeln für Potenzen:

$h\left(x\right)\ =0,25\cdot2^x=\frac{1}{4}2^x=\frac{1}{2^2}2^x=2^{-2}\cdot2^x=2^{x-2}$

Skizze:

(Das zeigt wieder einmal, dass es keine gute Idee ist, mit Dezimalzahlen zu hantieren)

Comments

[EinstNewt142]

Vielen Dank erstmal. Und woran erkannt man jetzt zum Beispiel an b) dass es eine Streckung in y Richtung ist und nicht in x Richtung. Weißt du vielleicht wo man das sieht?

[verreisterNutzer]

@EinstNewt142

Bei Aufgabe b)

Geh jeweils vom Scheitelpunkt genau 1 Einheit nach rechts und dann nach oben und zähle wie viele Einheiten Du nach oben musst, bis Du auf die Parabel triffst. Bei einer Normalparabel würdest Du genau 1 Einheit zählen. Sind es jedoch 2 Einheiten dann ist er Streckfaktor 2 und bei 1/4 Einheit bis nach oben ist der Streckfaktor 1/4. Deshalb ist g(x) = (1/4)· x² - 1 und h(x) = 2·(x - 2)² + 1

[EinstNewt142]

@verreisterNutzer

Dankeschön:) ich habe aber noch eine Frage. Wie erkennt man das a bei c) also quasi die Zahl oben vom Bruch, den Zähler. Auch eins nach links/rechts vom Asymptotenkreuz aus und dann zählen wie viel man nach oben/unten gehen muss, oder?