Was ist die Lösung zu dieser Frage?
Ein Dreiecken mit einem rechten Winkel, die beiden Seiten die an den rechten Winkel anschließen haben jeweils 25m und 37,5m Länge. Welche Seitenlänge und Flächeninhalt hat das größte Quadrat, was in dieses Dreieck hereinpassen würde?
4 Antworten
Sollte mit Strahlensatz gehen,
a/x = b/(b-x)
a und b die Katheten, x die Seitenlänge des Quadrats.
Satz von Pythagoras: a^2 + b^2 = c^2
Also die beiden seiten a und b quadrieren danach addieren, damit hast du die fläche c^2 und um die seitenlänge c zu berechnenen musst du nich die wurzel ziehen. :)
Ich brauche seitenlänge c aber nicht sondern die Seiten Länge des grösstmöglichen Quadrates das in das Dreieck hineinpasst
Oh sorry hab deine frage gar nicht richtig zuende gelesen, ich habe für die seitenlänge 15 bekommen. Brauchst du den lösungsweg?
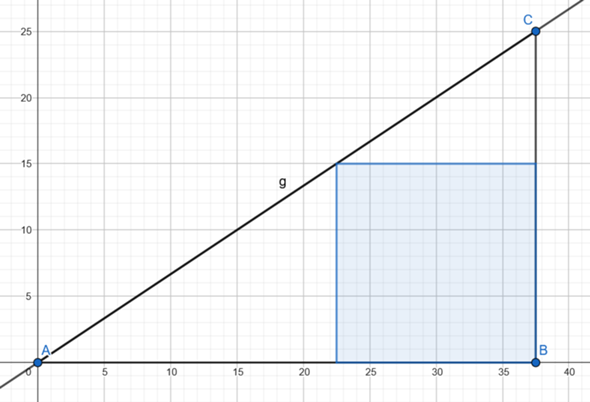
Die Gerade g durch die Punkte A und C ist die Funktion
y = 25/37.5 * x
Für ein eingeschlossenes Rechteck gilt dann:
h = 25/37.5 * x (Höhe)
b = 37.5 - x (Breite)
Weil das Rechteck ein Quadrat werden soll, muss gelten
h = b
25/37.5 * x = 37.5 - x
Lösung x = 45/2
Das Quadrat hat die Seitenlänge 37.5 - 45/2 = 15 und die Fläche 15².
Dieses Quadrat ist automatisch das grösst mögliche, weil bei einer Verschiebung von x nach links die Seitenlänge kürzer wird, und bei einer Verschiebung nach rechts das Quadrat aus dem Dreieck fällt.

Interessanterweise gibt es ein anderes Ergebnis, wenn man eine Seite des gesuchten Quadrats AUF die Hypothenuse legt. Wahrscheinlich ist aber wohl Deine Lösung gemeint, weil eine schön "glatte" Zahl rauskommt.
(Bei mir: 14,23 m).
Guter Hinweis! Danke dafür. Ich habe aber nochmal Glück gehabt, weil meine maximale Seitenlänge grösser ist.
...und die Lösung einfacher und schneller. Bei mir: 3 Gleichungen mit 3 Unbekannten
Trotzdem super, denn diese Möglichkeit habe ich übersehen. Eventuell gibt es Dreiecke, bei denen Dein Ansatz eine grössere Fläche ergibt.
Ich habe mir das Dreieck aufgezeichnet - so wie man es normalerweise macht mit der Hypothenuse nach unten. Dabei bin ich gar nicht auf die alternative Idee gekommen, das Quadrat an die beiden Katheten "anzuschmiegen".
Ich hab das mal nachgerechnet (mit Differentialrechnung, was ich bei der Aufgabenstellung zunächst erwartet hatte).
Es stellt sich heraus, dass die Lösung von Rammstein53 auch für andere Kathetenlängen das optimale Ergebnis darstellt - das (maximale) Quadrat, dessen eine Seite auf der Hypotenuse liegt, hat einen etwas kleineren Flächeninhalt.
Unter den Quadraten, die mit wenigstens 3 Ecken die Dreiecksseiten berühren, gibt es eins mit minimalem Flächeninhalt.
(Quadrate, die nicht alle Dreiecksseiten berühren, sind offensichtlich nicht maximal.)
Statt wenig hilfreicher Kommentare versuch ich mal, Dir wirklich "auf die Sprünge" zu helfen:
- Als erstes: Skizze machen mit dem gesuchten Quadrat innnen drin
- Du kennst beide Seiten vom großen Dreieck - also auch damit beide Winkel links und rechts der Hypothenuse.
- Diese Winkel tauchen aber auch auf in den kleinen Dreiecken die links und rechts vom Quadrat gebildet werden, in denen dann die Seitenlänge des Quadrats auftaucht.
- Damit hast Du 2 Gleichungen - Du brauchst aber drei: Die 3, Gleichung findest Du über die Länge der Hypothenuse des großen Dreiecks abzüglich der beiden Seiten der kleinen Dreiecke. Diese Differenz ist auch gleichzeitig die Seitenlänge vom Quadrat.
Die Fläche c² ? Meinst Du das etwa ernst? Was soll das?