Sinuskurve?

Wir haben gerade Sinusfunktionen in Mathe dran und ich verstehe das Thema auch. Was ich allerdings nicht verstehe ist, wie kann ich den Funktionsterm ablesen, wenn die x-Achse nicht mit Pi beschriftet ist, sondern mit normalen Zahlen? Da habe ich vor allem Probleme, wenn es um die Streckung an der x-achse geht. Danke schonmal für Antworten:)
2 Antworten
Ansatz: f(x) = a*sin( (b*(x+c) ) + d
Aus dem Graphen folgende Werte ablesen:
max: Maximum von f(x): 2.5
min: Minimum von f(x): -0.5
abs: Abstand zwischen zwei Minima oder Maxima: 3
ofs: erstes x >= 0 mit f(x) = (max-min)/2
hier gilt f(x) = 1 für x = 2, daraus folgt ofs = 2
Aus diesen Werten folgt:
a = 1/2*(max-min) = 1/2*(2.5 - (-0.5)) = 1.5
b = 2*π/abs = 2/3*π
c = -ofs = -2
d = max - a = 2.5 - 1.5 = 1
f(x) = 1.5 * sin( 2/3*π*(x-2) ) + 1

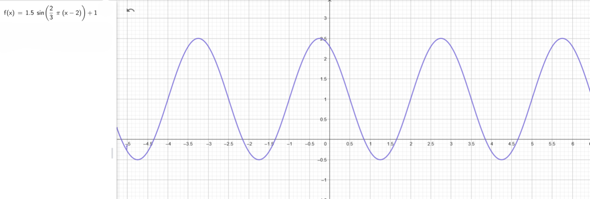
Die Periode p = 3 liest Du leicht als Differenz zweier Punkte auf der Mittellinie y = 1 ab. c = 1 / 2 liest Du dort ebenfalls ab. Die Verschiebung der Mittellinie von der x-Achse ist d = 1 und die Amplitude a = 3 / 2 ist der max. Abstand des Graphen von der Mittellinie. Und da die Kurve am Beginn der Periode (Schnittpunkt mit der Geraden y = 1) nach unten verläuft, kommt ein Minuszeichen davor.
allg.: f(x) = a * sin(b * (x - c)) + d
b = 2 * π / 3 = (2 / 3) * π
hier: f(x) = (-3 / 2) * sin((2 / 3) * π * (x - (1 / 2))) + 1