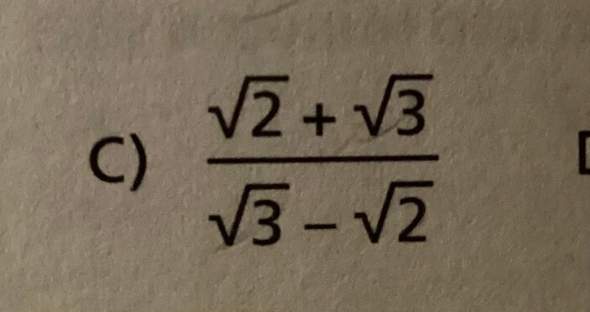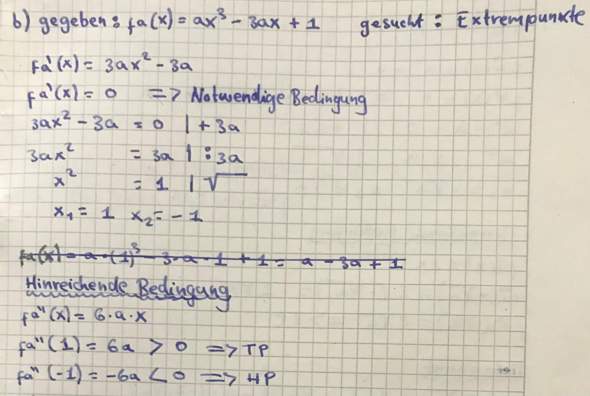Ich weiß nicht, ob ich richtig oder falsch gerechnet habe:
Wird ein Ball von einer Höhe von 2m in einem Winkel von 45° gegenüber der Horizontalen geworfen, so kann dessen Flugbahn mit dem Graphen der Funktion mit fv (x)=2 + x - 10*x2 /v^2 , v=R+ modelliert werden. Hierbei ist v (in m/s) der Betrag der Abwurfgeschwindigkeit, x (in m) die horizontale Entfernung vom Abwurfpunkt und fv (x) (in m) die jeweilige Höhe über dem Boden. Auf welcher Ortskurve befinden sich die Hochpunkte der Graphen?
Meine Lösung wäre wie folgt:
Tiefpunkt ausrechnen:
fv '(x)=1- 10 * 2x ÷ v^2
fv '(x)= 0 <= Als notwendige Bedingung
<=>0 =1- 10 * 2x ÷ v^2 |+1
<=> 1 = -10 * 2x÷ v^2 | *v^2
<=> v^2 = -10 * 2x |: (-10)
<=> v^2/ -10 = 2x | :2
<=> v^2/ -20 = x
fv ''(x)= -20*v^2 <= Als hinreichende Bedingung
f''(v^2/ 20) = -20* v^2 <= TP
fv (x)=2 + x - 10*x2 /v^2
<=> fv (v^2/ -20)=2 + v^2/ -20 - 10*( v^2/ -20)2 /v^2
<=> fv (v^2/ -20)= 2+ v^2/-20 - 10*v^4/ 400*v^2
<=> fv (v^2/ -20)= 2+ v^2/-20 - v^2/40
TP (v^2/ -20 | 2+ v^2/-20 - v^2/40)
Von x nach v umstellen:
v^2/ -20 = x |*(-20)
<=> v^2 = -20x
in y vom TP einsetzen:
g(x)=2+ -20x/-20 - (-20x/40)= 2+ x + 1/2x
das wäre dann die Ortskurve.
Jedoch ist man auf folgender Seite auf eine andere Lösung gekommen:
https://www.mathelounge.de/867065/auf-welcher-ortskurve-befinden-sich-die-hochpunkte-graphen
Mein Rechenweg jedoch basiert auf dieses Bild: