Momentane Änderungsrate und Hochpunkt, Hilfe bitte?
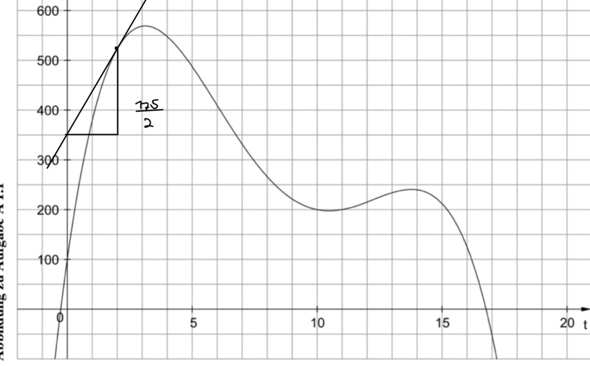
Hallo, in der Aufgabe c soll ich kurz um dass Maximum der Funktion n*t) bestimmen um zu wissen wann die Funktion ihre höchste Änderunsrate hat...jz steht aber in den Lösungen dass für t=15 die höchste Änderungsrate vorliegt... Ich versteh das nicht ganz, das Maximum ist doch bei t=3. Hängt das damit zsm dass t=15 ein Randextremum ist?


2 Antworten
Ist der Wert am Rand ein Extremum, muss ja dort nicht unbedingt die Steigung 0 sein. Man muss also diesen Wert mit dem innerer Extrema vergleichen, wenn nach dem größten wert gefragt ist.
Der Graph passt übrigens nicht zur Funktion.
Aso lol. Das klärt auch meine Frage weil das Randextremum bei t=15 im Bild sieht alles andere wie ein Hochpunkt aus. Hab mich einfach verlesen, vielen herzlichen Dank.
das Maximum ist doch bei t=3. Hängt das damit zsm dass t=15 ein Randextremum ist?
Ganz genau. Bei t = 3 haben wir nur ein lokales Maximum. Das globale Maximum liegt aber an der rechten Intervallgrenze bei t = 15. So sieht der Graph zu g(x) aus:
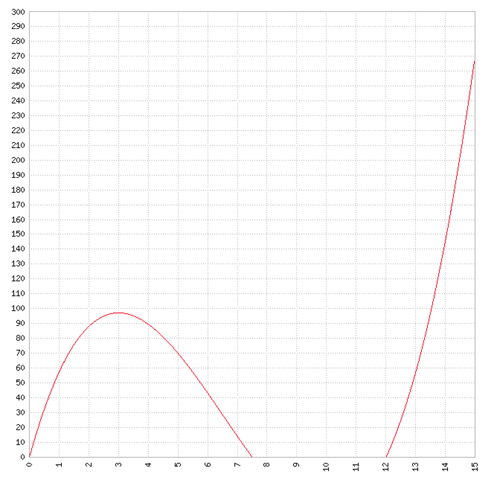
Aber wann soll ich wissen, dass ich die Randextremen miteinberechnen soll?
Das kann man vorher nie wissen.
Soll ich das einfach immer sicherheitshalber machen?
Genau das. Ist ja auch nicht sooo schlimm, die beiden Intervallgrenzen einzusetzen und mal eben auszurechnen.
Aber wann soll ich wissen, dass ich die Randextremen miteinberechnen soll? Soll ich das einfach immer sicherheitshalber machen?