Wo ist die zweite Nullstelle?
Aufgabe:
Die Absatzzahlen eines neu eingeführten Softdrinks können in den ersten zwei Wochen mit der Funktion: f mit f(x)=e^(x/2)-10x2+100x+50 (x in Tagen; f(x) Verkaufszahlen in Tausend pro Tag) modelliert werden.
e) Nach dem ersten Anstieg der Verkaufszahlen sinken diese wieder merklich. Um dem entgegenzuwirken, wird der Softdrink durch Werbemaßnahmen gestützt. Ermitteln Sie, zu welchem Zeitpunkt sich diese Werbemaßnahmen bemerkbar machen.
Ich wollte zu der Aufgabe den Tiefpunkt bestimmen, aber es kommt nur ein Hochpunkt bei x=5 raus, welcher auch richtig ist. Wo ist die zweite Nullstelle?
LG
2 Antworten
aber es kommt nur ein Hochpunkt bei x=5
x=5 ist doch auch nicht korrekt.
Die Ableitung der Funktion ist:
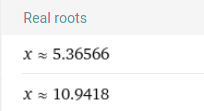
Die ganze Aufgabe lässt sich doch nur numerisch lösen. Und die beiden Nullstellen der ersten Ableitung sind:

bzw in exakter Form mit der Fortsetzung der ProductLog Funktion:


Eben, deswegen kannst Du das ja auch nicht auf dem Papier lösen und daher sind solche Aufgaben völliger Unsinn, weil Dir nur bleibt, die erste Ableitung in einen GTR zu werfen und zu schauen, ob und wenn ja, was der ausspuckt.
Hm na gut werde ich machen, danke!
Bei diesen blödsinnigen Aufgaben geht es ja darum, spezielle Punkte eines Funktionsgraphen in einen "Anwendungsbezug" zu packen. Ich gehe davon aus, dass hier ein Wendepunkt gesucht wird, da dort ja der Rückgang des Absatzes sich abschwächt.
Bei diesen blödsinnigen Aufgaben
Vollständige Zustimmung. Didaktischer Blödsinn.
PS: Übrigens hätte ich auch einen Wendepunkt im Sinne der Redendung "das Blatt hat sich gewendet" gesucht (denn hätte man dann auch noch analytisch bekommen).
Dachte ich auch in erster Linie, in den Lösungen steht aber ein Tiefpunkt??
Das verstehe wer will. Ich finde es jämerlich, wenn solche Unsicherheiten den eigentlichen mathematischen Kern in den Hintergrund treten lassen.
Ist eine Lösung mit GTR erwünscht?
Was ist denn numerisch lösen? Und was ist ProductLog? Hab das noch nie gehört