Mathe Integralrechnung?
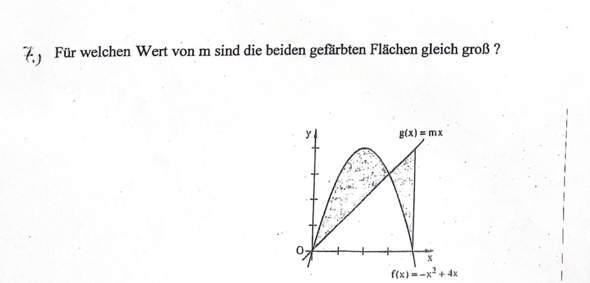
Auf der folgenden Seite sieht man einen Ansatz, den ich auch hatte und eine Lösung, die ich aber nicht verstehe.
https://www.mathelounge.de/766564/welchen-wert-mathrm-sind-beiden-markierten-flachen-gleich
Wäre nett wenn jemand entweder die Lösung auf der Seite erläutert, oder einen anderen Weg präsentiert. Ich komme nämlich nicht weiter.
An welcher Stelle der Lösung kommst du denn nicht weiter?
Die einzelnen Schritte verstehe ich rechnerisch, aber nicht Sinngemäß. Im Prinzip eine Erläuterung wieso man welchen Schritt geht
Ok, hast du dir denn die obere oder die untere Lösung/Antwort angeschaut?
Die obere hatte ich selbst. Aber das ist ja nur der Ansatz und bringt mich nicht auf 4/3 für m. Die untere ist die, die ich nicht verstehe
2 Antworten
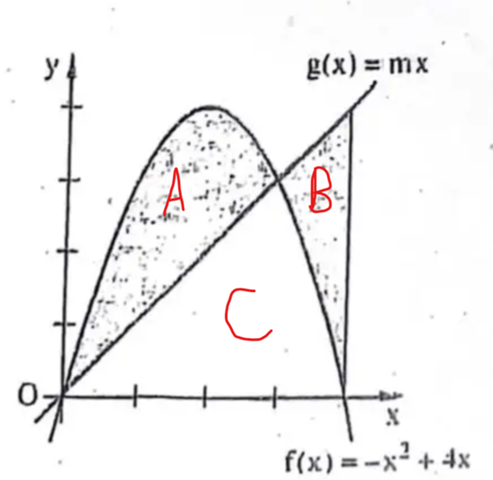
Ich habe die Flächen so benannt:
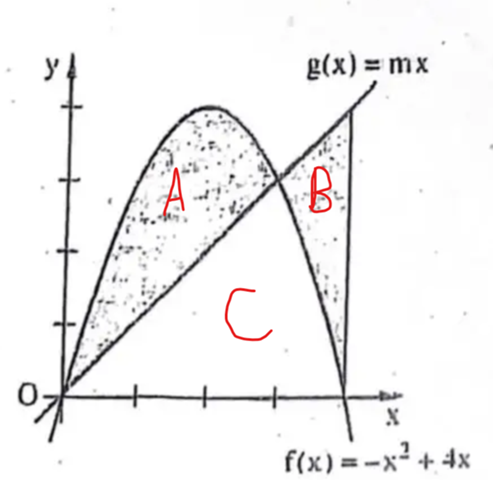
gesucht ist m, damit A=B gilt. Zunächst gilt:
A und B sollen gleich sein, also:
Kürzen nicht so wie ich vergessen! 4/3! :D
Um die Fläche zwischen den Graphen von zwei Funktionen f und g zu berechnet, kann man über die Differenzfunktion h=f-g integrieren. h gibt für jede Stelle x den Abstand zwischen den Graphen entlang der y-Achse an. Je nachdem, ob in einem Bereich f(x)>g(x) ist oder umgekehrt f(x)<g(x), ist h(x)>0 bzw. h(x)<0, also wird das Integral dann positiv oder negativ.
Geschickterweise sind hier zwei Bereiche im Spiel, in einem ist f(x)>g(x) und im anderen ist f(x)<g(x). Und die Beiträge der beiden Bereiche sollen vom Betrag her gleich sein. Somit wird das Integral über h insgesamt genau gleich Null sein.
Sagen wir, eine der beiden Flächen ist S, dann ist das Integral im linken Bereich S und im rechten Bereich -S, da hier h das genau entgegengesetzte Vorzeichen hat. Das Gesamtintegral über beide Bereiche ist deshalb S+(-S) = 0.
Macht es soweit Sinn? Wenn irgendeine Stelle unklar ist, frag gerne nach!
Danke, aber wie genau kommst du auf die Fläche B? Also 1/2 mal 4...