Wie komme ich auf die Lösung (Integralrechnung)?
Ich schreibe morgen eine Mathe-Arbeit und rechne gerade Übungsaufgaben. Jetzt soll ich hier eine Fläche berechnen, diese ist von der Funktion f, der y-Achse und der Geraden y=2 eingeschlossen.
Sprich die Pinke Fläche auf dem Bild:
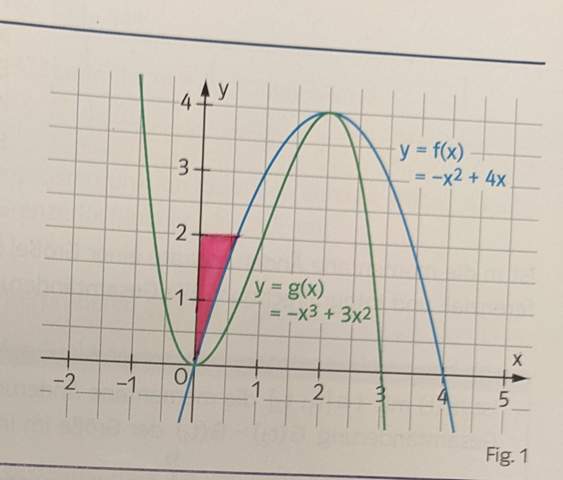
In der Lösung steht:
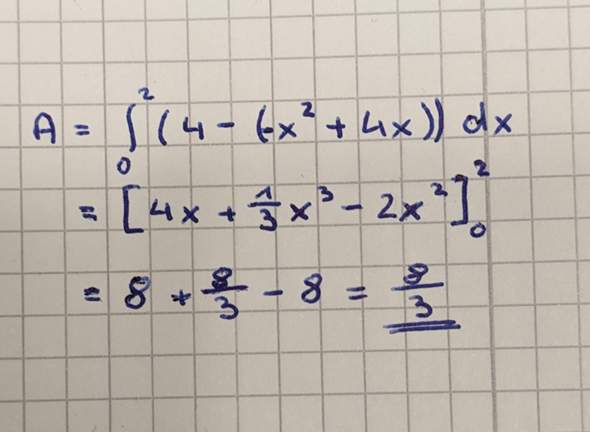
Wie komme ich vor allem auf diese 4 von der f(x) abgezogen wird? Das verstehe ich nicht
~ Schulbuch Mathematik (Bild oben) ist vom Klett-Verlag
3 Antworten
Die "Lösung" stimmt auf jeden Fall nicht.
8/3 sind ja fast 3, und die Fläche da ist nicht mal 1 groß.
Ich würde so vorgehen:
- Schnittpunkt von f(x) und 2 bestimmen. Das ist 2 - sqrt(2). Die 2. Lösung ist egal
- f(x) um 2 nach unten verschieben, dann musst du einfach nur das Integral bilden, da die Fläche durch die x-Achse begrenzt wird.
- Integral von f(x) = -x^2+4x-2 von 0 bis (2-sqrt 2)
- Da kommt das raus:
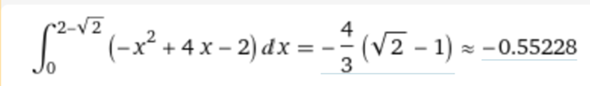
Weil wir die Fläche ja nach unten verschoben haben steht da jetzt ein Minus davor, also nehmen wir noch Betrag und haben die Lösung :)
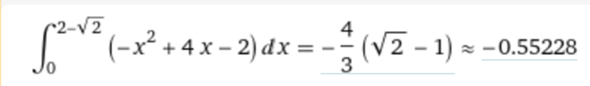
So ähnlich (nur mit Denkfehler) hatte ich es auch versucht, war dann aber verunsichert wegen der "anderen" Lösung im Buch....
Vielen Dank!
Vorwort : Die Lösung ist offensichtlich falsch ( wegen der 4 zb und der Obergrenze .
Sie bezieht sich auf diese
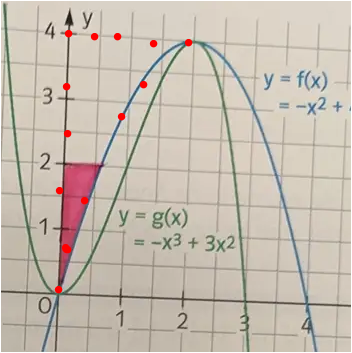
Fläche !
Zur Aufgabe :
zuerst 2 = -x² + 4x , den Schnittpunkt
0 = x² - 4x + 2
x1 2 = 2 + - wurz(4 - 2)
gebraucht wird 2-w(2) = S
.
Variante 1 :
Hier muss man vom Rechteck 2*S
die Fläche unter f(x) von 0 bis S abziehen
Int 0 to 2-2^0.5 f(x) = -x² + 4x = 0.61929
(2-2^0.5)*2 = 1.172
zusammen 0.5522 FE
.
Variante 2
Oder ein Abwasch
Int 0 to 2-2^0.5 f(x) = 2 - ( -x² + 4x ) =
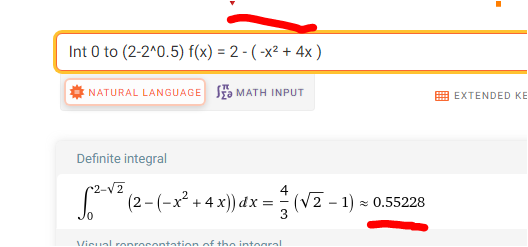
.
.
.
.
.
und so kann man sich versehen , wenn man die Schnittstelle für 0.5 hält :((
sah erst krass aus , aber hier kann man vom Rechteck 2*0.5 = 1 FE
die Fläche unter f(x) von 0 bis 0.5 abziehen
.
Int 0 to 0.5 -x² + 4x = 0.458333
macht insgesamt 0.5416666
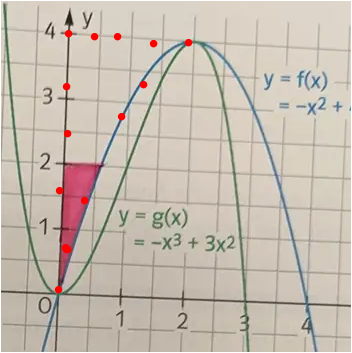
Die angegebene Lösung beschreibt das Integral bis zur Geraden y = 4. Das entspricht nicht der pink gekennzeichneten Fläche.
Nein, die Schnittstelle der Geraden mit der Funktion muss zunächst ermittelt werden als obere Schranke.
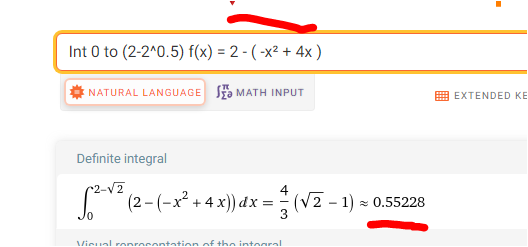
∫ (2 - (-x² + 4x) dx from 0 to 2 - √2 = 0,552285...
siehe Berechnung kaceye3003
Ergebnis stimmt überein.
Merke Dir einfach, dass die Schranken ermittelt werden müssen, wenn sie nicht gegeben sind. Das gilt auch für Nullstellen, wenn diese im Intervall liegen. Gute Nacht und viel Erfolg!
Heißt das für die Richtige Lösung müsste ich diese 4 durch eine 2 ersetzen?