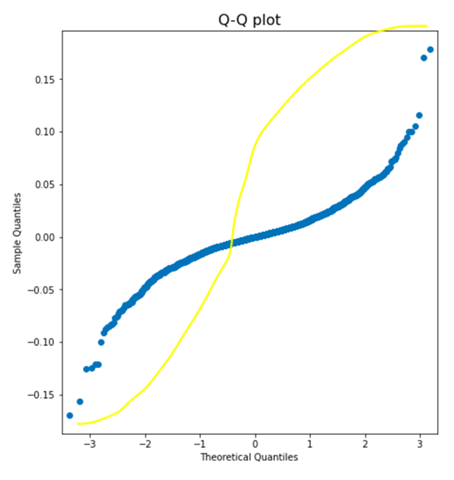
Shapiro Wilk oder kolmogorov-smrinov test?
um rauszufinden ob normalverteilung vorliegt
ich habe 2 stichproben, eine davon ist metrisch und eine ordinal und ich möchte kucken, ob es einen zusammenhang zwischen der ordinalen und metrsichen gibt, also ob die mittelwerte sich zwischen den ordinalen klassen unterscheiden oder nicht
wenn ich jedoch davor den test auf normalverteilung mache, macht man das ja für jede gruppe getrennt bezogen auf die metrischen stichprobe und bei dem kolmogorov smirnov test komme ich über all bei dem p Wert auf über 0,05 was bedeutete ich verwerfe nicht die nullhypothese und nehme eine normalverteilung an, jedoch ist bei dem shapirowilk test bei einer gruppe der p wert kleiner als 0,05, was mache ich da ?
ich habe eine stichprobengröße von 20 in der gruppe wo das nicht hinhaut insgesamt 55