A Teilmenge von B impliziert Komplement von B ist Teilmenge von Komplement von A?

Hey, stimmt die Implikationen oben? Wenn ja, dann bräuchte ich die für einen Beweis, also wäre super, wenn ihr mir sagen könntet, wieso die Implikationen stimmt oder woraus ihr das ableitet.

Dankeeeeeeee:D

Answer 1

[mihisu]

Sei Ω die Obermenge bzgl. der die Komplemente gebildet werden sollen.

Ja, für alle A, B ⊆ Ω gilt dann die Implikation...

$A\subseteq B \quad \Rightarrow\quad \Omega\setminus B\subseteq \Omega \setminus A$

Offensichtlich gilt (aufgrund einer gewissen Symmetrie, da das Komplement vom Komplement wieder die vorige Menge ist) sogar eine Äquivalenz...

$A\subseteq B\quad \Leftrightarrow\quad \Omega\setminus B\subseteq \Omega \setminus A$

Ein möglicher Beweis, bei dem einfach (nach Nutzung der Definition einer Teilmenge) ein wenig aussagenlogisch umgeformt wird...

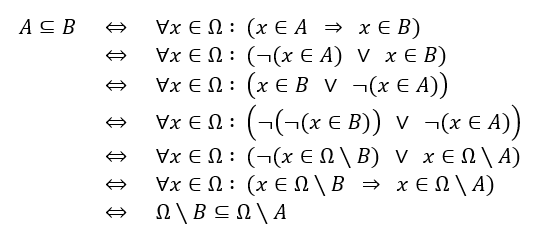
Bzw. entspricht diese mengentheoretische Äquivalenz quasi der aussagenlogischen Äquivalenz...

$\left(a\Rightarrow b\right)\quad \Leftrightarrow\quad \left(\neg b\Rightarrow \neg a\right)$

Comments

[Megalodon2002]

Wooow danke dir!!!!!!

Answer 2

[Maxi170703]

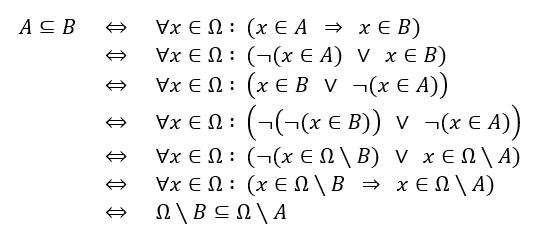
Ja ist wahr denke ich. Kannst du dir gut anhand der grafischen Darstellung von Mengen und Teilmengen und so herleiten. Zeichne dir das einfach mal auf, dann wird es offensichtlich.

Ein mathematischer Beweisversuch:

R steht für die Menge mit dem ,,Rest“

A = {a1,a2, …}
B = A U {b1, b2, …}
A^C = R\A

B^C = R\B = R\(A U {b1, b2, …}

Also B^C ,,Teilmenge von“ A^C, da alle Elemente von B^C in A^C

Woher ich das weiß: Studium / Ausbildung – Maschinenbaustudent, RWTH Aachen

Comments

[Megalodon2002]

DANKESEEE