Wie kann ich mit meinem Rechner (TI-30X Plus Multiview) Rechnungen folgenden Typs lösen? Ein Mann trinkt an einer Korbflasche Mineralwasser 21 Tage. Wenn jedoch seine Frau auch davon trinkt, reicht der Inhalt der Flasche für 14 Tage. Wie lange würde die Frau brauchen, um das Mineralwasser alleine zu trinken?

Und wie gehen die weiteren Aufgaben?

Also in einer Urne sind 2⚪️5🔵3🔴 kugeln also insgesamt 10  draus werden gleichzeitig 2  kugeln gezogen

Jetzt gibt es verschiedene fragen Beispiel
2 gleichfarbige kugeln
Jetzt hab ich  38/100 raus stimmt das oder nicht

Hallo ich habe heute meinen MSA in Mathe und bin immer noch nicht gut vorbereitet. Sollte ich heute krank machen, damit ich dann noch etwas Zeit zum lernen bis zur Nachprüfung habe ?

Wenn ich einen Punkt habe C(6/-3/6) und die Frage lautet ob dieser zwischen den Punkten A(2/-1/4) und B(-4/2/1) liegt, wie finde ich das raus?

Durch ein Sturm knickte eine Fichte 3.5 Meter über dem Erdboden ab. Die Baumspitze ist 8,5 m entfernt vom stehen gebliebenen Stammende aufgeschlagen. Wie hoch was die Fichte?

Hey, Ich habe glaube Ich hab schon eine halbe Ewigkeit damit verbracht diese Aufgabe zu lösen, und bin mir immer noch nicht sicher: Ein See ist 1,77km^2 groß. Seine Oberfläche wächst immer weiter mit einer schnellwachsenden Wasserhyazinthe zu. Die von ihr bedeckte Fläche verdoppelt sich alle 12 Tage. Im Moment sind 1/8 des Sees bedeckt. a) Wann ist die Hälfte des Sees bedeckt? b) Wann wird der ganze See bedeckt sein? Drücke deine Rechnung mithilfe einer Potenz aus.

a) 0T --> 1/8 12T --> 1/4
24T --> 1/2 --> Hälfte 36T --> 1/1 b) Ich hab hier ganz viel rumprobiert, bin aber auf nichts gutes gestoßen bsp: 1/812^2 1/82^2 1/8+2^12 1/8+12^2 1/82^12 1/812^2 Ich hab keine Ahnung, wie man Aufgabe b als Potenz angeben kann. Ich würde mich über eine verständliche Antwort freuen! LG Oskar

Hallo, ich habe hier Probleme bei diesen Sonderfällen beim herausfinden der Lösungsmenge. Es wäre nett, wenn .ur jemand weiter helfen könnte.

Jan ist 17 Jahre älter als Tarik UND 15 Jahre älter als Nadja. Zusammen sind alle drei 73 Jahre alt. Wie alt ist jeder?

Ich wollte fragen ob meine quadratische ergänzung stimmt und ob ich die klammern richtig gesetzt habe oder es fehler gibt

Ich muss die Funktionsgleichung der Gateway Arch bestimmen. Als info habe ich die höhe: 192 und breite 192 In der aufgabe steht dass ich auf dem 0 punkt stehe und sekrecht nach oben gucke.

Also,wenn man keine oder wenige richtige Ergebnisse hat aber jedoch die Rechenwege kann die Arbeit dann noch teilweise gut werden? Lg

Ein freundliches Hallo an alle Physik Experten da draußen,

als Hausaufgabe musste ich mal die Feldlinien einer Spule zeichnen. Nur leider hat die Lehrerin das ganze mit uns dann nicht mehr besprochen. Jetzt schreiben wir bald eine Arbeit und ich bin mir unsicher, ob meine Zeichnung richtig ist..

Könnte jemand vielleicht drüberschauen?

Meine Zeichnung findet ihr im Anhang.

Die kleinen Kreise sind die jeweiligen Magnetfeldlinienrichtung an der jeweiligen Stelle, die man mit der linken Hand bestimmen kann. Der Strom fließt von links nach recht. Links: Minus Pol, Rechts Pluspol

Ich bedanke mich im Voraus :)

Hey Community. :-) Ich bin vorherige Woche zufällig auf eine ganz interessante Matheaufgabe gestoßen. Ja - so weit so gut, leider fehlt mir jeder Lösungsansatz, da ich exponentielles Wachstum leider irgendwie komplett verdrängt hab.

Die Textaufgabe:

15 Ratten finden eine unbesiedelte Müllhalde, in der sie ideale Lebensbedingungen zum Fortpflanzen vorfinden. Der Zuwachs beträgt 4% vom Bestand. Gleichzeitig sinkt die Zahl der Ratten durch den Sterbefaktor mit 0,25% vom Bestand pro Tag.

Aufgabe 1: Wie viele Ratten leben nach einem Monat (30 Tage) auf der Müllhalde?

Aufgabe 2: Jeden Tag findet eine neue Ratte zufällig diese Müllhalde. Wie viele Ratten leben nach einem Jahr (356 Tage) auf der Müllhalde?

Aufgabe 3: Ein wildes Tier findet nach einem Monat (Aufgabe 1) die Müllhalde der Ratten & frisst jeden Tag 5 der Ratten. Wie viele Ratten sind nach einem Jahr (356 Tage) noch auf der Müllhalde?

Würde mich über hilfreiche Antworten/Lösungen freuen, denn mir fehlt ehrlich gesagt - jeder Lösungsansatz. :D

LG - Hanna

Formel X +X +Y : 2 -X ______ = X

Also, ich denke mir eine Zahl von 1-10 aus multipliziere diese ×2, rechne eine vom Trickvorführer genannte Zahl von 1-10 dazu, rechne das Ergebnis durch 2 und ziehe dann die von mir ausgedachte Zahl ab. Das Ergebnis kann der Trickvorführer dann nennen.

Wie funktioniert das, bzw nach welchem Prinzip muss man vorgehen?

Ich habe 5 Liter Tankvolumen ,muss Täglich 3.4km zur Arbeit hin und zurück (6.8 km am Tag ) Meine Frage wäre nun wie viele Tage reicht eine Mofatankfüllung etwa ? Ich kaufe mir bald eines und möchte das vorab herausfinden .Vielen dank :)

Ich konnte auf den ersten blick keinen finden.

Die Frage klingt ein bisschen blöd😂😅ABER
Habt ihr Ideen für Wörter die sehr schlau klingen.( Für einen TgA in deutsch )
Vielleicht eine besondere Form von einem Wort, welches man sehr häufig benutzt🙈
Bitte keine unnötigen Antworten geben🤦🏽‍♀️
Danke🙈❤

Ich zerbreche mir seit der Mathearbeit heute morgen nur noch den Kopf darüber..... Es war einfach nichts.. Es wurden nur vereinzelte Dinge vom Thema abgefragt die ich nicht wirklich konnte. Naja: Ich habe jetzt ein verdammt schlechtes Gefühl, vor allem nach dem ich mich mit meinen Kollegen auch noch über das Unterhalten haben, was sie als Lösung haben. Ich habe bisher eine 1- und 2- geschrieben und bei dieser Arbeit vermutlich steht ein Gegenteil bevor. Ich habe seit heute morgen schlechte Laune... Was tun? :/

Ich schreibe demnächst eine Mathe Arbeit über Potenzen und habe eine Aufgabe die ich rechnen können muss nicht verstanden. Die Aufgabe lautet: Gib 6,2 x 10^-4 cm in nm an. Und ich habe keine Ahnung wie ich das umrechnen soll bzw. wie das umrechnen der verschiedene Einheiten generell funktioniert.

H_a (untergestellt) ist 12 cm lang.
Und a ist 18 cm lang.
Meine Lösung für h= 15 cm
Und für s= 23,43 cm.

Danke,

Lg

Meine Frage lautet: " Berechne, wie viele cm2 Papier für die Banderole der Konservendose benötigt werden, wobei der klebefalz 1cm breit sein soll. Also die Mantelfläche M hab ich ausgerechnet und es kommen 400cm2 raus, aber wie rechne ich den Klebefalz mit?

"Die Wahrscheinlichkeit, dass sich beibringen neuen Auto innerhalb der ersten drei Monate ein Mangel herausstellt, liegt bei etwa 0,8%
A) in einer Woche werden 3210 Fahrzeuge fertiggestellt. Bei wie vielen dieser Fahrzeuge wird sich voraussichtlich ein Mangel herausstellen?
B) bei den Autos die montags das Band verlassen, ist die Wahrscheinlichkeit einer verarbeitungsfehlers doppelt so hoch wie an jedem anderen Tag. An jedem Arbeitstag (mo-sa) werden gleich viele Autos produziert. Wie viele Autos einer montagsproduktion werden vorraussichtlich einen Mängel aufweisen?

Bitte schnellstmöglich eine Formel. DANKE

Heyho,

gegeben sei folgende Aufgabe:

Für welchen Wert von k schließen die beiden Vektoren a = (k / 0 / -1) und b = (1 / √2 / -1) einen Winkel von 45° ein?

Habe versucht die Gleichung zur Winkelberechnung zu verwenden und nach k aufzulösen, jedoch kriege ich das nicht hin. Kann mir bitte jemand helfen?

Also ich weiß bisher das: 2 = 0.975^t Aber jetzt komme ich nicht bei " vierteljährlich " weiter ^^. DANKE! :)

Heyho,

folgende Aufgabe:

Betrag aus dem Vektor (k / -2k / 3)

Eingesetzt in die Betrags-Formel:

√(k²-2k²+3²) was gekürzt √(-k²+3²) ist. Und nu?

Gibt es einen Online-Taschenrechner, der sehr hohe Zahlen berechnen kann, ohne dass es ein Limit gibt?

Wie kommt es dann auf 40????

Ein Baum wird bei einem Sturm 8 m über dem Boden abgeknickt. Seine Spitze berührt in 15 Metern Entfernung den Boden.
Wie hoch war der Baum vor dem Sturm?
Bei mir kommt 12,7 m heraus, was laut den Lösungen aber nicht stimmt; was dann?

Danke!:)

Theoretisch könnte man ja einen Algorithmus programmieren, der alle Bilder, die ein Bildschirm darstellen kann, speichert o.ä. Wie viele Bilder wären das bei einer Auflösung von 1920x1080p und wie rechnet man so etwas aus? Und wie viel Speicherplatz bräuchte man dafür?

Wie weit kann man von einem 45m hohen Leuchtturm aus sehen, wenn man hinaus aufs Meer blickt? Die Erdkrümmung verhindert das man unendlich weit sehen kann. Stell dir die Erde als Kugel vor und nimm als Erdradius 6378km.

Ich habe zuerst die 45m zu den 6378km dazugezählt. Das wären ja dann 6378,045km. Dann habe ich den Satz des Pythagoras angewendet: 6378^2 + x^2 = 6378,045^2

Wenn ich das aber nach x auflöse kommt bei mir ein Betrag von 6378km raus, was ja falsch ist. Was hab ich falsch gemacht?

Könnt ihr mir weiterhelfen wie ich geographische Koordinaten(Längen und Breitengrade) in kartesische Koordinaten umrechne? Um genau zu sein habe ich die Koordinaten eines Landes und soll nun die Koordinaten umrechnen auf ein 3Dimensionales Diagramm. Der Radius ist mir ebenso gegeben. Danke im Voraus.

Beide Aufgaben 9. Klasse Gymnasium, Stoff Pyramide Oberflächeninhalt und Volumen

1: Eine gerade quadratische Pyramide der Grundkantenlänge 5,0cm hat ein Volumen von 50 cm³. Berechne den Oberflächeninhalt.

2: Eine 12cm hohe quadratische Pyramide hat das Volumen 1296 cm³. Welchen Summenwert haben die Längen aller Pyramidenkanten?

Ich hoffe mir kann jemanden weiterhelfen, da ich es auf Folie machen muss. Vielen Dank!!!

Die Anzahl der Besucher eines Schulfestes im Zeitraum von 7:30Uhr bis 16:30 durch die Funktion f mit f(t)=-t^3+24t^2-117t+182 beschrieben werden (t in std, t=7,5 entspricht der Uhrzeit 7:30 Uhr) a) Berechnen Sie, wann die meisten Besucher auf den Schulfest sind. b) Berechnen Sie, wann die Anzahl der Zuschauer am meisten zunimmt.

Hallo, in meiner Matheaufgabe steht, ich soll die Zeit Bereichen wie lange müsste ich fahren um die Route 66 an einem Stück ohne Pause durchzufahren.
Meine Angaben sind:

Strecke: 3944 km
Geschwindigkeit: 88 km/h

Ich weiß nicht wie ich es lösen soll, gibt es dafür eine Formel.

Hey
Ich bin schon eine weile an dieser Aufgabe (unten auf dem Bild zu sehen) und komme einfach nicht weiter. Wisst ihr wie man auf die Lösung kommt? Die Mittellinie kann ich problemlos berechnen aber wie erhält man die Höhe?
Lg

Ja oder nein Begründung bitte

Hey. mein Steam Account wurde vor paar Wochen gehackt, die E-Mail wurde geändert, aber zum Glück habe ich meinen Account wieder bekommen. Heute wurde mein Account wieder gehackt... Kann mir jemand eine Wahrscheinlichkeit angeben? Wird schwer aber unter euch gibt es bestimmt ein paar masterminds.

Hallo, also ich habe gerade Statistik und muss den Median mit mehr als 100 Zahlen berechnen und zwar schriftlich. Wie kann ich das machen ohne dass alles aufzuschreiben?

Danke im Voraus!

Hey ich hab eine Frage und zwar wie viele kanten, Flächen und ecken hat jeweils ein prisma mit der grundfläche zwanzigeck, 100-eck und 1000-eck. Ich komm mit diesen großen zahlen irgendwie so gar nicht klar bei der Grundfläche Dreieck, Viereck und Sechseck ging es noch voll. Ich bedanke mich schon mal für eure antworten.

Hallo.
Ich habe übernächste Woche mündliche Prüfungen und gehe in die 9. Klasse einer Hauptschule. Ist hier ein Hauptschulabsolvent, der mir den genauen Ablauf einer mündlichen Prüfung beschreiben kann? (In Mathe und in Deutsch, bei den anderen Fächern haben die Lehrer es uns erklärt.) Gerne mit jedem Detail, möchte mich wirklich gut vorbereiten.
Vielen Dank im Voraus

also ich soll die Rotationsmatrix in Bild 1 bestimmen und das habe ich in Bild 2 gemacht...

die Lösung mit genau diesen Vorzeichen finde ich in allen Internetquellen für den Fall, dass gegen den Uhrzeigersinn gedreht wird und das ist ja hier auch der Fall...

wenn ich aber nun z.B. für Phi 90° einsetze, kommt z.B. für xR= -yW raus und das ist ja nach der Abbildung ganz offensichtlich das falsche Vorzeichen, denn xR tritt ja dann an die Stelle von xW!

Wo ist der Fehler?

Ich soll einen Lückentext ausfüllen und stehe gerade auf dem Schlauch bei diesen Lücken:

Ein Punkt H (xH|yH) auf einem Funktionsgraphen heißt ____________, wenn yH der ____________ Funktionswert in einer Umgebung des Punktes ist.

Von einem ______________ steigt die Funktion, nach diesem fällt sie. Im _____________ selbst hat die Funktion die Steigung _________.

Kann mir jemand bei dieser Aufgabe helfen? Und zwar: Zwei Seilbahnstationen sind auf der Karte (Maßstab 1:50 000) 2,9cm voneinander entfernt. Das Halteseil ist 1500 m lang. Welchen Höhenunterschied überwindet die Seilbahn? Gibt es eine Formel oder so wie ich den Höhenunterschied berechnen kann?

Was ist der unterschied zwischen -5² und (-5)²? Weil wenn ich es in meinen Taschenrechner eingebe kommt das gleiche Ergebnis raus

Hallo :) Ich bin in der 9. Klasse eines Gymnasiums und muss eine Gfs über Quadratische Funktionen halten (das Thema ist für uns Wiederholung). Das Problem ist nur, dass ich generell in Mathe seeeehr schlecht bin und ich das alles auch nicht so ganz raff... Vor allem hab ich keine Ahnung wie ich die Präsentation gliedern soll... Ich hab mit meinem Lehrer gesprochen und er meinte, dass das alles reinmuss: - Besondere Punkte von quadratischen Funktionen - Symmetrieeigenschaften der Parabel - Funktionsterm und Graph einer quadratischen Funktion - Definitionsbereich und Wertebereich einer quadratischen Funktion Dann igwie noch folgende Eigenschaften: - Nullstellen und Linearfaktoren - Scheitelpunktsberechnung - Diskriminante, Lösungsmenge - und dann hat er noch gesagt, dass die Verschiebung wichtig ist (also dass ich dazu auch was sagen soll...) Ich wäre mega dankbar, wenn jmd ne Idee hat wie man das sinnvoll gliedern könnte, mit was ich anfangen kann damit alles sinnvoll ist und auch zu was ich vielleicht Übungsaufgaben in die Gfs machen könnte... Ich freue mich über ALLE ernsthaften Antworten :) Danke im voraus

Hallo. Ich habe nächsten Freitag Matheschularbeit und habe da eine wichtige Frage dazu. Und zwar weiß ich dass die Formel für die Funktionsgleichung y=kx+d ist aber wie komme ich auf k oder d wenn ich eine Gerade habe und das Steigungsdreieck einzeichne?

LG und danke für eure Hilfe Lisile

Ich halte meine Gfs in Mathe über Wahrscheinlichkeit und ich weiß nicht wie ich anfangen kann, also ich möchte nicht sagen: "hallo, ich halte meine Gfs heute in xy über das Thema xy".

Ich muss wine präsentation machen über das zylinder aber nur hauptsächlich volumen das ist mein unterthema . Könnt ihr mir mal alles aufschreiben was ich der klasse erzählen könnte . Ideen?

Ich programmiere gerade mit Java ein Plugin für einen Sponge Minecraft Server, und möchte es dem Assassinen ermöglichen, anderen in den Rücken zu stechen. Dazu mus ich feststellen, ob beim Damage Event der Schadensverursacher hinter der anderen Person steht. Wie mache ich das am besten? Ich habe die beiden Richtungen der Spieler als vector3d Variable, weiß aber nicht wie ich das machen soll, da ich nicht weiß wie man mit 3D Vektoren rechnet.

Code bist jetzt:

Player atk = p; Entity victim = p2; Vector3d position = atk.getRotation(); Vector3d location = victim.getRotation();

Ich entwickle aktuell mein erstes Spiel und benötige mathematische Unterstützung bei der Winkelberechnung. Dabei ist das Bild, was ich auf die schnelle in Paint gezeichnet habe, wichtig. Auf dem zweiten seht ihr das Spiel, man muss Coins einsammeln, dann kommt man in den nächsten level, hat 5 leben, 15 sekunden zeit pro level...ist halt mein erstes spiel :) die texturen/sprites sind auch erst einmal testweise drin und teilweise noch nicht selber gemacht, um erst einmal die Möglichkeiten zu testen, also nicht wundern ^^

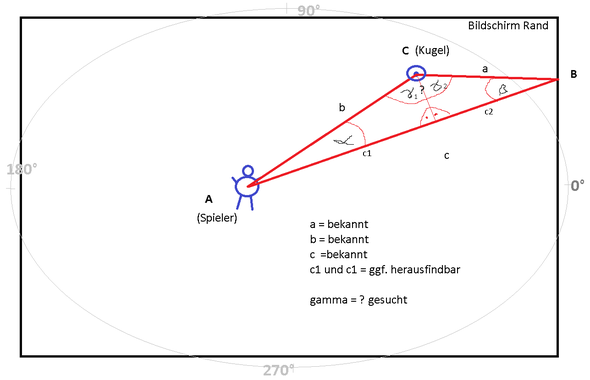
Wir haben eine Kugel bei C, die auf Spieler bei A abgeschossen wird. Nun ist es keine Kugel, sondern eine Patrone. Somit muss das Image gedreht werden, damit die Spitze der Patrone in schussrichtung zeigt (eine Patrone die Quer geschossen wird, sieht uncool aus ;)).

Das Image kann ich nach Grad drehen. Rechts ist 0°, oben 90°, links 180° usw., wie auf dem Bild zu sehen und durch den grauen Kreis dargestellt. Wenn die Kugel horizontal von rechts nach links geschossen wird, benötigt sie die Angabe 180°, um in Schussrichtung ausgerichtet zu sein.

Alles was ich benötige, ist der Winkel gamma (außer ich mache einen Denkfehler? müsste aber funktionieren, auch wenn ich ab einem bestimmten Wert die andere Seite des Winkels benötige). Dadurch dass ich die Position der Kugel und des Spielers im Raum weiß, kann ich die Seitenlängen a, b, c berechnen. Wahrscheinlich kann ich auch c1 und c2 berechnen, falls es mich weiterbringen sollte, bin mir da aber noch nicht sicher.

Ich habe eine hilfslinie eingezeichnet, um rechte Winkel zu bekommen. Dadurch könnte ich gamma1 und gamma2 berechnen, diese addieren und dadurch hätte ich das, was ich benötige. Aber ich weiß nicht wie und sitze schon ein paar stunden daran.

Soweit meine recherchen ergaben, kann ich mit den aktuellen Informationen diese Aufgabe nicht lösen.Welche Werte benötige ich, um gamma herausfinden zu können? Eventuell kann ich diese Werte programmiertechnisch herausfinden. Allerdings beschränkt es sich eher auf entfernungen (längen), außer ich übersehe etwas.

Kann mir jemand helfen? :)

Beim schreiben ist mir aufgefallen, dass wenn ich c1 und c2 habe, ich tatsächlich gamma1 und gamma2 berechnen und addieren kann. Das müsste soweit laufen. Dann muss ich jetzt herausfinden, wie ich an c1 und c2 komme. Gibt es eventuell einen einfacheren Weg? Die Berechnung wird sonst immer komplexer und somit ressourcenfressender

Hallo! Ich schreibe bald eine Mathearbeit und das Thema sind Wahrscheinlichkeitsrechnungen. Ich war hier grade am üben und habe folgende Frage vor mir:

In einem Strumpf befinden sich 5 farbige Kugeln, darunter eine gelbe. Wie hoch ist die Wahrscheinlichkeit, dass die gelbe Kugel beim vierten Zug gezogen wird?

Ich weiss zwar wie hoch die Wahrscheinlichkeit ist, dass die gelbe gezogen wird ich weiss aber nicht wie man die Wahrscheinlichkeit ausrechnete, dass sie beim vierten Zug gezogen wird.

Kann mir jemand erklären wie das geht?

Welches Einfluss hat jeder einzelne Parameter auf die Funktion?

f(x)=a*ln(bx^2+c)+d

Hi

Ich möchte eine beliebig hohe Zahl von Nachkommastellen berechnen, speichern und ausgeben können, allerdings rundedt Python immer von allein auf 16 Stück ab. Wie kann ich dieses Runden umgehen, sodass mind 50 Nachkommastellen angezeigt werden?

VG

Von einem rechtwinkligen Dreieck kennt man die Eckpunkte A(-4I-2) B(5I1) und C(1I?) Gesucht ist die fehlende4 Koordinate C der rechte winkel befindet sich beim Eckpunkt A weiters sind die anderen beiden Winkel gesucht diese sollen mithilfe der Vektorrechnung berechnet werden. Danke im voraus! :)

Kann man als Maschinenbaulehrer Mathematik unterrichten?

Ich muss da etwas in Abhängigkeit von a ausrechnen und da kommt bei mir das hier raus:

s = √{(1/2 * √{a² + a²})² + (2a)²}

Diese Klammer {...} soll die Wurzel darstellen, da ich nicht weiß, wie ich das auf dem Computer schreiben soll. Ihr seht hier also eine große Wurzel, in der sich eine weitere Wurzel befindet √{...√{...}...}

Im Ergebnis steht aber folgendes: s = 3/2*√{2a}

Es ist so, dass es schon länger her ist, dass wir das hatten und kommende Woche schreibe ich meine Abschlussprüfungen. Ich bin mir ziemlich, dass wir es nicht exakt genauso wie im Ergebnis darstellen müssen, aber ich bräuchte Hilfe dabei, wie man das etwas genauer zusammenfassen kann.

Wie ist das mit den Wurzeln und dem Quadrat? Wann heben die sich gegenseitig auf (schließlich habe ich ja mehrere Quadrate in der Wurzel)? Was würdet ihr als nächstes tun, um mein Ergebnis näher zusammenzufassen?

Hier ist die Aufgabenstellung:

31.0 Das Quadrat ABCD (Seitenlänge a) ist Grundfläche einer Pyramide mit der Höhe h = 2a, deren Spitze S senkrecht über dem Diagonalenschnittpunkt M des Quadrates ABCD liegt.

(31.1 Zeichen Sie ein Schrägbild der Pyramide für a = 6 cm; ω = 30°; q = 1/2; [AB] liegt auf der Schrägbildachse.)

31.2 Bestimmen Sie die Länge s(a) der Seitenkante sowie den Flächeninhalt S(a) einer Seitenfläche in Abhängigkeit von a.

[Ergebnis: s(a) = 3/2*√{2a}, S(a) = √{17}/4*a²]

Hallo zusammen, bin derzeit in der Q1 in NRW und hatte vor Physik zu studieren. Stehe im Mathe LK zwischen 2 und 3 und im Physik LK zwischen 1 und 2 obwohl ich nicht viel lerne (vlt. halbe Stunde die Woche). Ist für mich ein Physikstudium machbar ? Ich liebe Physik echt total , Mathe hingegen ist ok, es stört mich jetzt nicht aber macht mir auch nicht besonders viel Spaß. Vor allem wie hoch ist der Lernaufwand, grade in den ersten Semestern? Wäre nett wenn ihr mir eure Erfahrungen berichten könntet.

Danke im Voraus.

Gegeben sei D(4I9) sowie B(8I5) und e=AC(Vektorstrich drüber)=6*Wurzel 2 bestimme die fehlenden 2 Punkte Vielen Dank im voraus!

Hi, hätte eine kurze Frage zum o.g. Thema. Ich übe für meine Klausur und eine Frage ist:

Geben sie eine Zahl aus dem Intervall [0,1] an, die sich nicht Mit dem IEEE Standart als 32 Bit Gleitkommazahl darstellen lässt begründen Sie Ihre Antwort.

Komme da einfach nicht weiter, Hilfe wäre super!

Kann man Aussagen darüber machen wie viel Prozent von einem Stoff nach der hälfte der Halbwertszeit zerfallen sind ?

Ich soll die Länge des Schlauches berechnen wenn ich 20 ml Chloroform destillieren möchte , der Schlau ist 2 mm breit.

Hiernach soll ich auflösen/πr²•h=20 cm³

H ist gesucht.

Bitte so einfach erklären wie es geht .

Danke

Ich muss als Hausaufgabe ein Rezept mit der Schlüsselzahl umrechnen, doch ich verstehe das nicht. Das Rezept ist für 12 Portionen und soll auf 10 Portionen umgerechnet werden.

Rezept:

Für dem Teig: 200g Mehl 80g Zucker 90g Butter 1 Ei

Für die Füllung: 50g Zucker 2 Eier 40g Speißestärke 1/2L Milch 1 Vanilleschote

Danke schon mal im Voraus

Eine Ware wiegt verpackt 34.6kg. Tara: 1.45kg. Bruttopreis der Ware: Fr. 15.50/kg. a) Gesamtpreis der Ware? b) Nettogewicht in kg? c) Nettopreis pro kg?

BItte mit Lösungsweg und keine Antworten wie; Gehe googeln oder so was!!! danke :=)

danke!

Also im Buch steht: Multipliziert man eine natürliche Zahl mit der um 10 größeren Zahl, so erhält man 704. Wie lautet die Zahl?

Naja, eigendlich bin ich gar nicht so schlecht in Mathe, aber die hier verstehe ich nicht. Kann mir das jemand erklären?

Bei einer Schnitzeljagd starten drei Gruppen an den Gekennzeichneten Punkten A(0,0) B(7,17) C(7,-17)

Bestimmen Sie die Koordinaten des Ziels Z, wenn alle drei Gruppen durch gleichgroße Entfernung von Start und Zielpunkt gleiche Siegchancen haben sollen.

Hallo, ich stehe nun vor der Wahl meines Studiums und gleichzeitig ein Schritt in die Zukunft und des Erwachsenwerdens .

Ich interessiere mich für diesen Studiengang, neben ein paar anderen und würde auf eure Meinung mal gerne freuen zu lesen .

Was kann man danach interessantes machen ? Welche attraktiven Masterstudiengänge bieten sich an ?

Ist der Studiengang denn auch ausreichend um danach einen guten Job zu bekommen ?

Wie fandet / findet ihr das Studium ?!

Für wen ist dieses Studium gar nicht gemacht ?

( in Mathe bin ich eher mittelmäßig wollte ich hinzufügen , kreatives denken und präsentieren und Kontakt mit Menschen sind eher meine Stärken )

Eventuell Studierende  aus dem Rhein Main Gebiet hier ?

Hallo zusammen,

ich habe ein ziemliches Problem. Es geht um Mathe. Ich habe zwei Funktionenscharen, nämlich ft(x) und gt(x). ft(x) = 1+tsin(x) gt(x) = (1/πt)x^2-(1/t)*x+1 Ich muss jetzt die Schnittpunkte der beiden Graphen finden, besser gesagt eine Formel für die Schnittpunkte. Ich weiß, dass ich ft(x) und gt(x) gleichsetzen muss, aber wie komme ich von dort aus auf die Schnittpunkte? Es erscheint mir extrem schwer, bei so einer Gleichung nach x aufzulösen, und was muss ich mit dem t machen?

Hey könnt ihr mir helfen?

Drei Freunde, Viviana, Laura und Lennert, gewinnen bei einer Lotterie 2400€. Lennart bekommt 300€ mehr als Laura und Viviana bekommt halb soviel wie Laura und Lennert zusammen. Nun soll man für alle drei Terme aufstellen und in einer Gleichung lösen. Aber ich weiß nicht wie ich vorgehen soll.

Wenn ich sage das Lennert = x ist Laura = y und Viviana = z ist, dann müssten ihre Terme so aussehen :

x = 2400 - (y+300) y = 2400 - (x-300) z = 2400 - (x+y)/2

Aber wie gehe ich weiter vor?

Danke für eure Hilfe

Hallo,

ich habe folgende Aufgabe erhalten und leider keine Lösungen.

Ich habe folgendes bei a gemacht.

a) 12.000+4000+1200+800=18.000/1100=16,36

b) 200*16,36 Euro = 3.272 Euro.

Stimmt sowas?

Ich würde gerne euch im Hilfe fragen. Vielen Dank.

Marc

Hallo,

ich habe die untenstehende Aufgabe und keine Lösungen hierzu.

Könnte mir jemand helfen und diese Aufgabe erklären?

a) Gewinn 60.000 Euro habe ich berechnet. Also Deckungsbeiträge (Summe) - Fixkosten d. h. 880.000 Euro - 820.000 Euro = 60.000 Euro.

Aber wie berechne ich den durchschnittlichen Break-Even-Umsatz?

Danke

Würde mich freuen, wenn mir jemand helfen könnte. vielen dank und schönen feiertag. Marc

Ein radioaktives Präparat zerfällt so, dass seine Menge stündlich 8,3% abnimmt. Nach wie vielen ganzen Stunden ist erstmals weniger als 1 Zehntel der Anfangsmenge vorhanden?

Ich würde gerne wissen wie ich das rechnen muss, aber eine Lösung würde auch reichen

München liegt am Breitengrad 48,1 wie berechne ich den radius von münchen den ich brauch um die bahngeschwindigkeit zu berechnen?

Die Steigung eines geradlinigen Straßenstücks beträgt 7%. Bestimme den zugehörigen Steigungswinkel.

Also, die Antwort kenne ich ja schon. Sie beträgt 4°. Nur ich brauche einen Rechenweg, wie man den Steigungswinkel bestimmen kann.

Könnt ihr mir helfen bitte. 

Hallo,

ich habe folgende Aufgabe gerechnet, siehe unten Bild.

Ich habe folgende Ergebnisse;

a) Gewinnschwelle: 400 Stück.

b) Kosten und Erlöse gleich hoch.

c) ca. 428 Stück (Gerundet)

d) 307 Stück gerundet.

Ich wollte euch fragen, ob ich hier richtig gerechnet hab, hab leider krumme zahlen raus, deshalb frage ich um Unterstützung.

vielen Dank.

marc

hey, dieser Körper besteht ja aus 2 Kugeln. Das Volumen habe ich so berechnet: Volumen der einen Kugel durch 2 minus das Volumen der anderen halbkugel. und wie mache ich es bei der oberfläche? Die oberfläche der grösseren halbkugel minus die der kleineren? ich denke das ist nicht richtig.... habt ihr ideen?

Hi Leute, ich hab Probleme die folgenden Bedingungen abzufragen. Kann mir jemand zumindest eine Aufgabe lösen, damit ich einen Ansatz habe und es eventuell verstehen kann.

Getestet werden soll (mit if-Abfrage), ob - eine Variable i ein ganzzahliges Vielfaches von 5 ist - eine Variable x im Bereich [10, 20] liegt (einschließlich der Grenzen)

Wenn man zB die funktion f(x) =1/3^3 -2,75x^2+6x+2 hat und einen näherungswert für die steigubg an der stelle x=4,5 nenen muss wie löst man so eine aufgabe? Was bedeutet win näherungswert?

Hat jemand die Lösung?

Versteht das jemand

Ich habe mich vor gut einem Jahr viel mit Ellipsen beschäftigt. Da es zur Berechnung des Umfangs einer Ellipse noch keine exakte Formel gibt, lediglich Annäherungsformeln, war es mein Ziel eine eigene Annäherungsformel zu finden. Nach einigen Versuchen habe ich dann etwas herausgefunden, was logisch scheint. Die formel lautet für a und b jeweils die geraden die durch den ellipsen mittelpunkt gehen (und zusammen einen 90 grad winkel ergeben): u=pi*b-(b-a)/2 grund: ich habe durch probieren herausgefunden dass man mit der formel b-(b-a)/2 die mitte zwischen zwei zahlen erhält. jetzt stellt es euch mal vor: a, die kleinstmögliche gerade in der ellipse und b die größtmögliche treffen sich in der mitte: heraus kommt der durchmesser eines kreises der den gleichen umfang wie die elipse haben müsste. wenn b sich um die menge verkleinert in der sich a vergrößert dürfte das auf den umfang keinen einfluss haben. ich habe diese formel sonst nirgendwo gefunden also bin ich vermutlich der erste der sie entdeckt hat. außerdem habe ich sie mit einer anderen annäherungsformel verglichen (die ich mit meinem geringen mathematischen wissen als 10klässler, damals 9klässler allerdings nicht verstehe) und der unterschied im ergebnis betrug gerundet nur etwa eine differenz von 1. die frage ist, was mache ich mit dieser formel? jkann ich patent für sie setzen oder gibt es eine bestimmte person an die ich sie schicken kann oder ähnliches? danke schon mal im vorraus

Hey, ich bringe mir gerade das Lösen von LGS mittels Gauß Verfahren bei. Das kann man ja auch in Gleichungen aufschreiben und dann ganz normal lösen durch Umformungen.

2x - 5y + z = 9 

.

x + 6y - z = - 7 

.

- 3x + 1y - 2z = - 8

.

Die Lösung müsste sein

x = 1 y = - 1 z = 2

Ich versuche seit 4 h auf dieses Ergebnis zu kommen. Formal sind mir alle Umformungsregeln bekannt. Aber an irgendwas hapert es dennoch, ich komme einfach nicht auf die Lösung und werde langsam wahnsinnig.

Kann mir bitte jemand den Lösungsweg darstellen bzw. erklären worauf man achten muss... bei der Lösung stoßt ihr evtl. auf 19 y und 17 y innerhalb des LGS,... an dieser Stelle jedenfalls komme ich jedenfalls nicht mehr weiter...

Ich bin sehr dankbar für Rat!

Hallo Liebe Menschen da draußen. Wer hat Lust zu rechnen? :))Leider kann ich den Bruch nicht hereinkopieren... Kann mir hierbei Jemand mit dem genauen Rechenschritt behilflich sein? Es wird nach der Definitionsmenge und der Probe gefragt.

(17x-5/15x+5)+(13x-1/6x+2)=(7x-3/3x+1)+1

Bei einer Stehleiter mit 3m langen Holmen ist die Sperrkette ausgehängt. Der anfängliche Öffnungswinkel gamma der Leiter beträgt 30 Grad .Wie hoch befindet sich anfangs das Gelenk g der Leiter über dem Boden? G ist ganz oben auf der Leiter also ist nach der Höhe gefragt! Ich komme aber trotzdem nicht weiter.