Berechnung der Trapezfläche dank Strahlensätze?
Hey
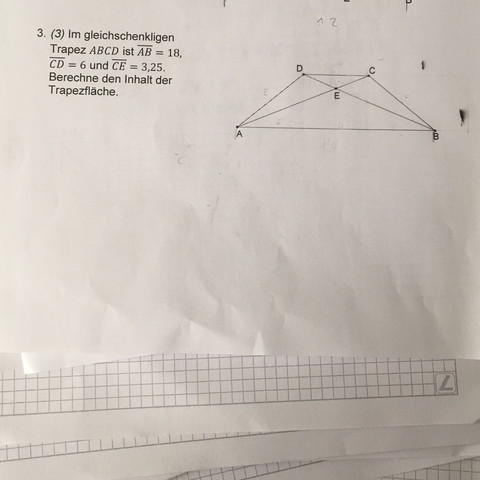
Ich bin schon eine weile an dieser Aufgabe (unten auf dem Bild zu sehen) und komme einfach nicht weiter. Wisst ihr wie man auf die Lösung kommt? Die Mittellinie kann ich problemlos berechnen aber wie erhält man die Höhe?
Lg
4 Antworten
DC/ AB = CE / AB
6 / 18 = 3,35 / x
x = 18 * 3,25 / 6 = 9,75
AC = AE + CE = 9,75 + 3,25 = 13
Wenn CC' die Höhe ist dann haben wir :
BC' = (18 - 6) /2 = 12/2 = 6 =>
=> AC' = 18 - 6 = 12
CC' ² = AC² - AC'²
CC'² = 13² - 12² = 169 - 144 = 25
CC' = √25 = 5
A = (18 + 6) /2 * 5 = 12*5 = 60 Einheiten²
AB = a, CD = c
Die beiden Diagonalen bilden den Schnittpunkt E.
Für den Abstand E zur Linie c (absE) gilt
(A) absE = h * (c + 2a) / ( 3 * (a+c) )
(A) h = absE * ( 3 * (a+c) ) / (c + 2a)
Ausserdem gilt
(B) absE² + (c/2)² = CE²
(B) absE = wurzel ( CE² - (c/2)² )
Aus (A) und (B) kann man h berechnen
Mittels Strahlensatz kannst Du AE berechnen. Zeichne jetzt noch die Höhe durch E ein. Die halbiert die Seiten AB und CD, weil das Trapez gleichschenklig ist. Es entstehen daher vier rechtwinklige Dreiecke, von denen Du jeweils zwei Seiten kennst - die fehlende Höhe ergibt sich mittels Pythagoras. Damit kannst Du die Gesamthöhe des Trapezes ermitteln.
Hallo,
hier noch ein Lösungsvorschlag (mit Zeichnung) zur Berechnung von h.
h = h₁+h₂+h₃
1) h₂ mit Pythagoras:
h₂² + 3² = 3,25² => h₂ = 1,25
2a) EB mit Strahlensatz:
EB/3,25 = 18/6 => EB = 9,75
2b) h₃ mit Pythagoras
h₃ = = EB² - 9² => h3 = 3,75
3) h₁ mit Strahlensatz:
h₁ / (h₁+h₂+h₃) = 3/9 = 1/3 <=> 3h₁ = h₁+h₂+h₃ <=>
2h₁ = h₂+h₃ = 1,25 + 3,75 = 5 => h₁ = 2,5
Daraus folgt
h = h₁+h₂+h₃ = 2,5+1,25+3,75 = 7,5
Gruß

Ich Esel: h₁ braucht man ja garnicht!
h = h₂+h₃ , also 3) kann man sich sparen.
Wenn ich einmal in Schwung bin, berechne ich alles, was nicht bei drei auf den Bäumen ist. *lol* :-)
Gruß