Hi,
verwende einfach die 3. binomische Formel:
a² - b² = (a - b) (a + b), wobei:
a =der erste Ausdruck mit den Variablen xyz und b = der zweite Ausdruck.
Verstehst Du wie ich meine, dass Du die Aufgabe aangehen sollst?
LG,
Heni
Hi,
verwende einfach die 3. binomische Formel:
a² - b² = (a - b) (a + b), wobei:
a =der erste Ausdruck mit den Variablen xyz und b = der zweite Ausdruck.
Verstehst Du wie ich meine, dass Du die Aufgabe aangehen sollst?
LG,
Heni
... obwohl es 47 Jahre her sind, dass ich die Schule beendet habe. :-)
Hi,
da kann ich weder für Bukarest noch für Kiel abstimmen.
Ich stamme aus Rumänien und bin jetzt auch in Rumänien, allerdings ganz im Westen (Timisoara) und 500 km von Bukarest. Jetzt um 17:45 (Ortszeit) sind hier 40°C, auf Dauer macht das kein Spaß, ist also nicht auszuhalten. Das Wetter ist so hier seit circa 2 Wochen.
Also weder Kiel noch Bukarest!
LG,
Heni
Hi Marlene,
(siehe Bild):

LG,
Heni
Hi,
der Text der Aufgabe ist falsch (die Funktion) und das ist in der Lösung nicht der Fall.
Die Funktion lautet: 1/2 * x² (x + 5), denn x + 5x macht da keinen Sinn, klar wäre es 6 x so wie auch Du es gerechnet hast.
LG,
Heni
Ab der 1. Klasse. Schon dann war ich "überzeugt", dass ich Mathelehrer werden will.
Hi,
das kannst Du egal mit welcher Funktion machen, klar ist die gekürtzte dann vorteilhafter.
LG,
Heni
Das ist die Zeit in der ein Formel I Fahrer mit 360 km/h genau 1 cm zurücklegt!
Das Licht legt in derselben Zeit circa 30 km zurück!
Hi,
das stellt man am besten mit einer Tabelle dar:
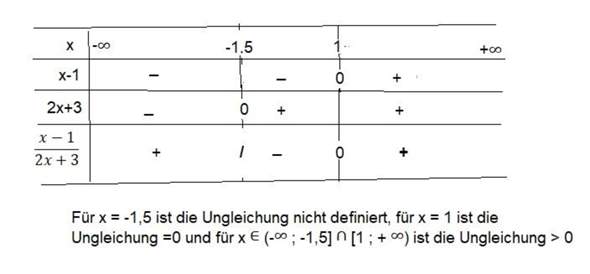
LG,
Heni
Hi,
wenn das = Zeichen dabei ist, dann muss es auch nach Umkehrung der Ungleichung dabei bleiben:
LG,
Heni
..... die Amis zum Besipiel schreiben zuerst den Monat dann den Tag im Datum!
LG,
Heni
Hi,
100% - 3% = 97% = 0,97
Endbestand (nach 20 Minuten)= 80 * 0,97^20 = 43,5 g!
LG,
Heni
Hi,
ungerecht ist es nicht, aber es könnte besser sein!
LG,
Heni
Hi Hanni,
um welche Klasse geht es da? Das Dokument sieht so aus, als würde es um ein Studium auf der Uni gehen, was Mengenlehre betrifft.
Es sieht aber eher aus nach Einführung in Mengenlehre.
habe hier die Aufgaben gelöst (hoffe ich verstehe nichts falsch?)

LG,
Heni
Hi,
glaube nicht dass es zu einem Weltkreig kommt; die Gefahr ist aber da und laut Militärexperten ist diese höher als sie im kalten Krieg war.
LG,
Heni
Hi,
Länge ist 2x + 1, wenn Du für x = 5 seinsetzte ergibt das:
2 * 5 + 1 = 10 + 1 = 11
Breite ist x = 5
F = L * B = 11 * 5
LG,
Heni
Hi,
der satz von Vieta gilt in allen Zahlenmengen, ganze Zahlen, rationale Zahlen, irrationale Zahlen und auch außerhalb der Menge der reellen Zahlen, also in der Menge der komplexen Zahlen!
LG,
Heni
Hi,
das sind 5 h + 45 min = 5 * 60 + 45 min = 300 min + 45 min = 345 Minuten
LG,
Heni
Hi Selina,
sagen wir mal
8² = 64
64 kann man zum Beispiel schreiben:
64 = 36 + 28
√36 = 6
√28 = 5,3 (ungefähr).
Also Hypotenuse ist 8, Kathete 1 = 6, Kathete 2 = 5,3
LG,
Heni
Hi,
ich schätze mal, wenn die Leute sich die Hände reichen, haben sie alle eine Spanne von circa 1,30 Meter. Also 40.000.000 : 1,3 = 30, 7 Millionen Menschen.
LG,
Heni