Baumdiagramm – die neusten Beiträge

Zwei Würfel werden gleichzeitig geworfen. Ich soll die Wahrscheinlichkeit berechnen, dass die Augensumme kleiner als 9 oder größer als 6 ist.

Für kleiner 9 habe ich insgesamt 26 Möglichkeiten erhalten, also ist die Wahrscheinlichkeit 26/36 und für größer 6 habe ich 21 Möglichkeiten erhalten, also ist die Wahrscheinlichkeit 21/36.

Hier überschneiden sich doch die Wahrscheinlichkeit, oder etwa nicht? Ich habe also eine Schnittmenge, die nicht nur die leere Menge enthält.

Wie berechne ich das also? Ich kann die Wahrscheinlichkeit ja nicht einfach addieren da komme ich auf >1.

Wenn auf Wikipedia folgendes steht:

Ist mit paarweise disjunkt dann gemeint, dass die Ereignisse stochastisch unabhängig voneinander sind oder hab ich was falsch verstanden?

Lg

Die gegebene Aufgabe ist: Eine Urne ist mit q schwarzen und r roten Kugeln befüllt. Es wird mit Zurücklegen und ohne Berücksichtigung der Reihenfolge gezogen.

Wie hoch ist die Wahrscheinlichkeit, beim Ziehen von l+m Kugeln genau l schwarze und m rote Kugeln zu ziehen?

Mein 1. Ansatz:

Einführen einer Zufallsgröße X, die die schwarzen gezogenen Kugeln zählt und binomialverteilt ist mit n = q+r und p = l/(q+r). Die gesuchte Wahrscheinlichkeit ist nun P(X=l). Ist dieser Ansatz so korrekt?

Mein 2. Ansatz:

Prinzipiell kann man ja auch damit arbeiten, dass bei Laplace Experimenten die Wahrscheinlichkeit berechnet werden kann, indem man die Anzahl an günstigen Ergebnissen durch die Anzahl an insgesamt möglichen Ergebnissen teilt.

Es gibt insgesamt (q+r)^(l+m) / (l+m)! Möglichkeiten, aus q+r Kugeln genau l+m Kugeln auszuwählen (mit Zurücklegen und ohne Berücksichtigung der Reihenfolge).

Es gibt (q)^(l) / l! Möglichkeiten, aus q Kugeln genau l Kugeln auszuwählen. Und es gibt (r)^(m) / m! Möglichkeiten, aus r Kugeln genau m Kugeln auszuwählen. Folglich gibt es ((q)^(l) / l!) * ((r)^(m) / m!) Möglichkeiten, aus q schwarzen Kugeln genau l schwarze Kugeln und gleichzeitig aus r roten Kugeln genau m rote Kugeln auszuwählen (mit Zurücklegen und ohne Berücksichtigung der Reihenfolge. Die Terme sind analog zum Fall ohne Zurücklegen und ohne Berücksichtigung der Reihenfolge aufgestellt).

D.h. die gesuchte Wahrscheinlichkeit lässt sich auch als

(Möglichkeiten, aus q+r Kugeln genau l+m Kugeln auszuwählen)/(Möglichkeiten, aus q schwarzen Kugeln genau l schwarze Kugeln und gleichzeitig aus r roten Kugeln genau m rote Kugeln auszuwählen)

= ( (q+r)^(l+m) / (l+m)!) /
((q)^(l) / l!) * ((r)^(m) / m!) ) ausdrücken, oder?

Ist das so korrekt, oder sind mir irgendwo Fehler unterlaufen? Sind beide Ansätze zulässig?

Hi,

ich weiß nicht, wie wahrscheinlich das ist, aber damals mit 12-13 war ich in meinem Klassenzimmer und hatte einen Würfel in der Hand. Ich hab ungefähr 25 mal eine 6 hintereinander gewürfelt. Ich find es - wenn ich zurückdenke - schon ziemlich krass. Wie selten ist sowas ? Und wie wahrscheinlich ist das ?(das denke ich mir nicht aus, es ist wirklich passiert)

Guten Abend,

ich würde mich sehr über eure Hilfe zur Aufgabe b) freuen. Ich komme leider auf das Ergebnis, dass 25 % der Urlauber bis 60 Jahren eine Reise über das Internet buchen. In der Musterlösung stehen jedoch 29,76 %.

• Habe ich hier einen Fehler bei meiner Vierfeldertafel gemacht?
• Ist hier die Vierfeldertafel überhaupt möglich?

Ich freue mich sehr auf eure hilfreichen Antworten.

Hallo, ich habe folgende Aufgabe:

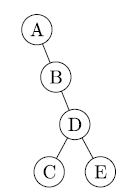
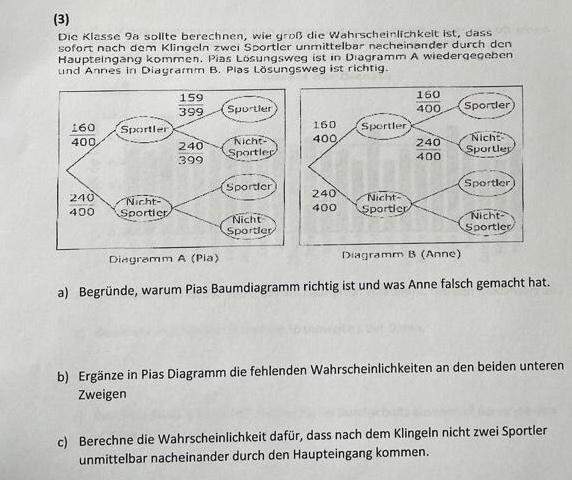
Gegeben sei der folgende Suchbaum, in dem die Elemente A;B;C;D;E

lexikographisch geordnet sind. Beweisen oder widerlegen Sie:

Der Baum kann ein optimaler Suchbaum mit 2,1 erwarteten Vergleichen sein.

Da kommen ich und viele andere nicht weiter, die meisten neigen zur Meinung, dass die Aussage falsch ist. Wir haben dazu sehr viele Gleichungen aufgestellt, die aber kompliziert zu lösen scheinen: (a bis e sind die jew. Zugriffswahrscheinlichkeiten)

a+b+c+d+e=1

a+2b+4c+3d+4e=2,1

Durch die e_ij Tabellen (erwartete Anzahl Vergleiche im Unterbaum von i bis j):

b<=a, e<=d<=c

Aber ich stecke jetzt fest wie ich hier wirklich weiterkomme. Muss ich etwa noch mehr Ungleichungen/Gleichungen aufstellen?

Vielen Dank im Voraus!

Aus einer Urne mit 3 roten und 4 schwarzen Kugeln werden nacheinander 3 Kugeln entnommen, wobei jede mögliche Auswahl von 3 Kugeln die gleiche Wahrscheinlichkeit besitzen soll. An bezeichne das Ereignis, dass sich unter diesen 3 Kugeln genau k rote Kugeln

befinden (k = 0,1,2,3). Berechnen Sie die Wahrscheinlichkeit dieser Ereignisse, wenn

die jeweils entnommene Kugel wieder zurückgelegt wird,

die entnommenen Kugeln nicht zurückgelegt werden.

Ich Brauche Hilfe bei dieser Aufgabe. Die Aufgabe a) habe ich noch hinbekommen danach kam ich nicht mehr weiter. Vorallem die d) bereitet mir Schwierigkeiten.

Kann mir da jemand helfen?

Hallo, ich habe hier eine Aufgabe und die heißt die vier Felder Tafel zeigt die Ergebnisse einer Untersuchung zu Handynutzung und Intelligenzquotienten.
Prüfen Sie ob die Ereignisse A „eine zufällige, ausgewählte Person hat einen IQ >130“ ist und B „eine zufällig ausgewählte Person nutzt das Handy intensiv“ , Stochastik unabhängig sind ,in dem sie A Wahrscheinlichkeiten PA(B) und P(B) berechnen.

ich füge die Aufgabe noch mal im Bild hinzu, die vier Felder Tafel wurde schon angegeben. Wie muss ich denn jetzt die Aufgabe lösen? Ich brauche da wirklich Hilfe weil ich schreibe in zwei Tagen Klausur

In einer Tüte sind 5 rote und 7 grüne Gummibärchen. Du nimmst nacheinander zwei Gummibärchen heraus. Jedes Gummibärchen, das du herausnimmst, futterst du sofort auf.

a) Erstelle ein zugehöriges Baumdiagramm.

b) Mit welcher Wahrscheinlichkeit hast du jeweils eines von jeder Farbe gegessen?

c) Mit welcher Wahrscheinlichkeit hast du erst ein rotes dann ein grünes

Gummibärchen verputzt?

d) Wie groß ist die Wahrscheinlichkeit, dass alle von dir verspeisten Gummibärchen die gleiche Farbe hatten?

Ich habe einen Würfel mit 8 Seiten, die Zahlen gehen von 1 bis 8. Ich würfel 3 mal. Wie viele Varianten gibt es höchstens 13 zu erhalten?

Kann mir jemand bei der Aufgabe helfen ich komm da nicht weiter das ist ne Übung für die Klassenarbeit und ich bin wirklich am verzweifeln ich verstehe das nicht. Ich danke im Voraus

Aufgabe:

Eine Münze wird dreimal nacheinander geworfen. Stelle das Zufallsexperiment in einem Baumdiagramm dar. Bestimme für das angegebene Ereignis die Wahrscheinlichkeit seines Eintretens.

(1) zuerst Wappen, dann zweimal Zahl

(2)nicht dreimal Wappen

(3)der letzte Wurf ist Zahl

(4)mindestens einmal Wappen

(5)mehr Wappen als Zahl

(6) gleich oft Wappen und Zahl

(7) Pasch (d.h. drei gleiche Ergebnisse)

(8) höchstens zweimal Zahl

(9) der erste Wurf ist Wappen

(10) der zweite Wurf ist Zahl

Hallo,

es gibt ja totale Wahrscheinlichkeiten in der ersten Stufe eines Baumdiagramms, bedingte Wahrscheinlichkeiten in der zweiten Stufe eines Baumdiagramms und UND-Wahrscheinlichkeiten in der dritten Stufe eines Baumdiagramms:

Gibt es auch vierstufige Baumdiagramme mit bedingten Wahrscheinlichkeiten in der zweiten und dritten Stufe? Wie sieht dann das Formelzeichen für die bedingte Wahrscheinlichkeit in der dritten Stufe aus? Und wie berechnet man die Wahrscheinlichkeiten in der dritten und vierten Stufe dann?

Danke für Hilfe!

Aufgabe 1

b) Wie viele dreistellige Zahlen gibt es?

Eine Reißzwecke wird dreimal geworfen. Die Wahrscheinlichkeit dafür, dass sie auf dem Kopf liegen bleibt, beträgt 0,55. Berechne die Wahrscheinlichkeit für die Ereignisse:

a) Genau zweimal auf dem Kopf landen".

b) Genau einmal auf dem Kopf landen.

c) höchstens dreimal auf dem Kopf landen"

d) Reißzwecke landet dreimal auf dem Kopf.

e) „Mindestens zweimal auf dem Kopf landen".

Abbildung 1 zeigt einen Teil eines Baumdiagramms zu einem 4-stufigen Experiment mit einer Urne. In der Urne liegen 4 rote und 6 grüne Kugeln. Das Ziehen einer roten Kugel wird als Erfolg gewertet.

1. Ergänzen Sie das Baumdiagramm so weit wie möglich.
2. Berechnen Sie die Wahrscheinlichkeit dafür, dass bei einer Kette zunächst zweimal eine rote und dann zweimal eine grüne Kugel gezogen wird, also (r,r, g, g).

Ich komme bei dieser Aufgabe nicht weiter und würde mich sehr über Hilfe freuen, weil ich die Lösungsschritte gerne nachvollziehen wollen würde

Ich sitze nun schon seit über einer halben Stunde an dieser Aufgabe und komme nicht weiter. Laut Lösungsbuch sollte eine 0.47%-ige Wahrscheinlichkeit herauskommen allerdings verstehe ich nicht wie man darauf kommt.

Danke im Voraus für eure Hilfe!

In einer Urne liegen 2 Rote und 3 blaue Kugeln. Es werden zwei Kugeln ohne zurücklegen gezogen. E: Zu 60% wird genau eine rote Kugel gezogen. Was ist davon die Gegenwahrscheinlichkeit?

Ich bin über jeden Tipp dankbar, viele Grüße.

Hallo alle zusammen, ich war die letzten Tage krank und habe dieses Arbeitsblatt zu Wahrscheinlichkeiten gemacht und bin mir bei einigen Sachen nicht sicher und wollte fragen ob jemand es bitte sich ein mal anschauen könnte ob es stimmt. Schönen Tag noch und danke im voraus.

60% der 25 Schülerinnen und Schüler einer Klasse sind Mädchen. Neun

besitzt.

Schülerinnen haben ein Haustier, während bei den Jungen jeder fünfte ein Haustier

1. Erstelle eine Vierfeldertafel mit absoluten Werten
2. Wie viele Jungen haben ein Haustier?
3. Wie viel Prozent der Kinder der Klasse besitzen ein Haustier?
4. Ein Kind ohne Haustier wird zufallig ausgewählt. Wie groß ist die Wahrscheinlichkeit, dass es ein Junge ist?
5. Erstelle zu d) ein Baumdiagramm mit relativen Haufigkeiten und markiere die gesuchte Häufigkeit im Baumdiagramm.

Wie hoch ist die Wahrscheinlichkeit bei 3 Würfen 2 Zahlen außer 6 doppelt zu haben.

Ich habe als Ergebnis 13,9% aber glaube es ist Falsch

Also akzeptable Ergebnisse sind zum Beispiel:

6,5,5

1,3,3

5,4,5

Und wie hoch ist die Wahrscheinlichkeit, dass keine Zahl doppelt vorkommt. (Mein Ergenis = 55,6%)

Diese Frage wurde bereits beantwortet, vielen Dank an die die mir geholfen haben!

Die Anzeige eines Glücksspielautomaten besteht aus neun Leuchtfeldern, die mit den Ziffern 1 bis 9 beschriftet sind.

Nach Einwerfen des Spieleinsatzes leuchten zufällig genau vier Felder auf.

Alle Kombinationen sind gleich wahrscheinlich. Die leuchtenden Ziffern ergeben von links nach rechts gelesen eine vierstellige Zahl.Der Automat wirft am Ende eines jeden Spiels so viele Euro aus, wie die Endziffer der leuchtenden Zahl angibt.Wie viele Euro muss der Spieleinsatz betragen, damit das Spiel fair ist?

Ich weiß, dass der Gewinn mindestens 4€ - Einsatz beträgt, und dass der Erwartungswert 0 sein muss. Ich weiß aber nicht, wie wahrscheinlich die einzelnen Ereignisse sind, da die Zahlen nicht nebeneinander aufleuchten müssen.

wenn man zum Beispiel eine bin Verteilung hat die die Wahrscheinlichkeit für die Anzanl von richtigen Antworten angibt, also laut unserer Lösung muss man wenn man wissen will wie hoch die Wahrscheinlichkeit ist, dass der Schüler 5 und mehr antworten richtig hat die Wahrscheinlihckeiten mit dieser formel von bernoulli oder so ausrechnen, aber das ist doch doppelt gemoppelt, wenn ich 5 antworten richtig habe, dann ist das ja in 6 antworten schon drinne, und die 6 ist in der 7 drinne

also wieso summiert man das trotzdem

bei a.) (80,5%) komme ich aufs richtige Ergebnis, aber bei b.) nicht

1. Wäre es falsch, die Äste w und s (rot eingezeichnet) an den Ast r anzuhängen? Es heißt ja, dass die rote unter beiden Zügen erscheinen soll? Deswegen sind doch meine rot eingezeichneten Pfade doch noch notwendig?
2. Und warum addiert man zu P (X = -0,8€ also „rote Kugel unter den beiden gezogenen Kugeln“) die WSK 1/8 dazu (dort ist ja die rote Kugel NUR in einem Zug enthalten)? Das ist doch falsch?

Bitte um Hilfe! Danke!

Könnt ihr bei Aufgabe 3 helfen

Hallo, Ich habe ein Problem in Mathe(A2) und finde nichts zu einer Lösung.

Wie kann man hier vorgehen, mein Baumdiagramm wird nur unendlich lang.

Vielen Dank

Könntet ihr mir bei c) und d) weiterhelfen?

Hallo, kann mir jemand sagen, ob mein Resultat richtig ist? Ich habe leider keine Lösungen dazu, daher kann ich es nirgends nachschauen...

danke im Vorraus

Aufgabenstellung: In einer Schachtel befinden sich 2 grüne Kugeln sowie je 1 schwarze, 1 rote und 1 blaue Kugel.

Nun zieht man 3 Kugeln aus der Schachtel, ohne dass eine gezogene Kugel wieder zurückgelegt wird. Berechnen Sie die Wahrscheinlichkeit, dass mindestens 1 grüne Kugel dabei ist

Mein Resultat ist 0.1, im angehängten Bild sieht man den Lösungsweg.

Angenommen man schießt 5 mal mit einer Waffe, jeder schuss hat die wahrscheinlichkeit von 10% ein fehlschuss zu sein.

Wie würde die formel lauten um die wahrscheinlichkeit auszurechnen für genau einen fehlschuss, egal der wie vielte schuss es war?

und dann wie würde die formel aussehen dafür dass der fehlschuss an einer bestimmen stelle sein soll, also zum beispiel der 2. oder 4. oder was auch immer?

(bitte ohne binomialverteilung falls möglich)

Woher weiß ich wie viele Kombinationen es gibt mit 3 Würfeln maximal eine 9 zu Würfeln? Ich weiß, dass es 81 sind aber ich weiß nicht wie man darauf kommt.

Vielen Dank im Voraus

Der Anteil der 18-24-Jährigen an allen Personen mit einer Fahrerlaubnis lilegt in Deutschland bei etwa 9,7 %. Die Wahrscheinlichkeit für einen Unfall mit Personenschaden liegt bei etwa 0,9% pro Jahr, Die Gruppe der mindestens 25-Jährigen stellt pro Jahr 89,58 % aller Personen, die kelnen Unfall mit Personenschaden haben,

a) Erstellen Sle eine Vierfeldertafel mit den relativen Häufigkeiten

b) Zeichnen Sie ein Baumdiagramm, in dem zunächst nach Alter verzweigt wird.

c) Entschelden Sie, welche Personengruppe lm Straßenverkehr gefährdeter ist.

Wie erstelle ich dazu eine vierfelder Tafel? Mein Ansatz wäre links das Alter und oben unfall oder kein unfall mit Personenschäden aber dafür fehlen mir Infos und wie bringe ich die 9,8% ein?

Hi,

ich habe zurzeit das Thema Wahrscheinlichkeit in der 10. Klasse in Mathe und weiß nicht genau, wie ich folgende Aufgabe lösen soll:

Die Wahrscheinlichkeit, dass eine junge Frau an Brustkrebs erkrankt ist, liegt bei 0,8%. Ein Brustkrebsindikator stellt bereits vorhandenen Brustkrebs zu 99,9% fest, dagegen stellt er keinen Brustkrebs zu 96,8% fest.

Ich soll zu dieser Aufgabe zuerst eine Vierfeldertafel erstellen. Also mit den Kategorien Krebs, nicht Krebs, Brustindikator positiv und Brustindikator negativ.
Aber wie erstelle ich nun so eine Vierfeldertafel aus den Werten. Kann mir jemand weiterhelfen?

Vielen Dank im Voraus!

LG

Irgendwas stimmt nicht, Hilfe

Ein fairer roter und ein schwarzer Würfel werden auf einmal geworfen. Bestimme die Wahrscheinlichkeit

1. mit einem Würfel Sechs und mit dem anderen Würfel Eins zu werfen;

Stimm es wenn ich sag, die Sechs kann beim roten ODER schwarzen Würfel vorkommen, das heißt 1/6 +1/6 und für die Eins bleibt dann nur mehr ein Würfel übrig also (1/6 + 1/6) * 1/6

Welche Formel muss ich hierfür verwenden?

Welche Formel wird für diese Aufgabe verwendet?

Hallo Ihr Lieben, ich brauche bitte Hilfe bei dieser Rechnung. Es geht um Binomialverteilung🫣die Aufgaben B und C ganz unten auf dem Zettel finde ich am schwierigsten, also die kleinen Buchstaben …. Vielleicht könnt ihr mir Ansätze geben, wie ich das einfach lösen kann, da ich das bis morgen haben muss. Das wär sehr nett..

danke

Beim Spielbeginn braucht man eine Sechs, um eine Figur auf das Startfeld stellen zu können. Hat man keine Figur im Feld, so hat man drei Versuche, um eine sechs zu würfeln; glückt hier keine sechs muss man bis zur nächsten Runde warten.

Miriam behauptet:,,Schau wir sind vier Spieler, und da muss man davon ausgehen, dass einer von uns im ersten Durchgang nicht raus kommt.“

Berechne die Wahrscheinlichkeit, dass alle vier in der ersten Runde nicht ,,rauskommen“.

Wenn eine Münze von 3 Würfen 2x davon auf der selben seite landet. Wieso ist dann die wahrscheinlichkeit dafür 3/4.

Ich hätte gesagt: Beim ersten werfen ist die WS 1/2 beim 2. Wurf wieder da sich die WS ja nicht verändert und beim letzten Wurf auch wieder 1/2...

Bin bei Wahrscheinlichkeit bei den Bernoulli Ketten und weiß nicht mehr wie man das eintippt kann mir bitte jemand helfen

Guten Tag,

kann mir jemand hier bei dieser Aufgabe weiterhelfen, wie man hier am besten vorgeht?

Hallo allerseits!

Ich bin grade dabei Mathe für eine Arbeit zu lernen zum Thema Wahrscheinlichkeitsrechnung. Eigentlich kann ich das ganz gut nur habe ich durch die Ferien länger nichts mehr dazu gemacht. Es würde mich freuen wenn ihr mir zu der Aufgabe helfen könntet:

Konstantin und Rosanna treten gegeneinander im Torwandschießen an. Jeder hat 5 Schuss. Konstantin weiß das seine Trefferquote bei 25% liegt. Rosanna trifft im Normalfall 3 von 10 Schüssen. Bestimme die Wahrscheinlichkeit dass...

A) Rosanna beim vierten Schuss zum ersten mal trifft.

Aufgabe B und C würde ich gerne selber machen da ich glaube, dass diese mir klar werden, sobald jemand A löst. Die Aufgaben müssen im Baumdiagramm aufgezeichnet werden es wäre als hilfreich (nicht nötig) wenn ihr das auch so machen könntet.

Vielen Dank im Voraus!

Wenn ein Flug 100 gebuchte Passagiere hat und im durschnittliche 2 Leute nicht erscheinen. Mit welcher Wahrscheinlichkeit kommen alle 100, bzw. Was ist überhaupt die Wahrscheinlichkeit für das Fehlen von 2 passagieren

In 10 Muffins werden 50 Himbeeren verteilt. Wie groß ist...

A die Wahrscheinlichkeit, dass in einem Muffin gar keine Himbeeren sind.

B die Wahrscheinlichkeit, dass in einem der Muffins mindestens 10 Himbeeren enthalten sind.

Möchte den Lösungsweg zu dieser Aufgabe verstehen, also bitte erklären, vielen Dank

Danke im Voraus :)

Hallo Zusammen,

kann mit bitte Jemand bei folgender Kombinatorik Aufgabe helfen, wie man auf die Lösung 56 kommt?

"Drei nicht unterscheidbare Würfel werden geworfen. Wie viele verschiedene Augenkombinationen gibt es?"

Meiner Meinung nach können bei einem Wurf sechs verschiedene Seiten/Zahlen geworfen werden. Das würde aber bei drei Würfen 6^3 machen?

Ein Verkehrsunternehmen gibt an, dass 85% seiner Fahrgäste zufrieden sind.

a) Bestimmen Sie die Wahrscheinlichkeit, dass von 50 Fahrgästen höchstens drei mit dem Verkehrsunternehmen unzufrieden sind.

b) Berechnen Sie, wie viele Fahrgäste mindestens befragt werden müssen, damit mit einer Wahrscheinlichkeit von mindestens 90% mindestens zehn davon unzufrieden sind.

Beim Cross Bowl wirft man stoff bälle möglichst nahe an eine rote Ziel Kugel. ida trifft die Kugel durchschnittlich in zwei von zehn fällen.

A) ida wirft einen Ball. Mit welcher Wahrscheinlichkeit trifft sie die Zielkugel nicht?

B) Ida wirft nacheinander zwei Bälle. Mit welcher Wahrscheinlichkeit trifft sie die Kugel genau einmal?

In einer Urne befinden sich 10 blaue, 4 rote und 6 grüne Kugeln. Es werden 2 Kugeln gezogen mit zurücklegen.

1. Zeichnen Sie das Baumdiagramm.
2. Berechnen Sie die Elementarereignisse. Runden Sie dabei auf 3 Stellen nach dem Komma.
3. Wie groß ist die Wahrscheinlichkeit, dass 2 grüne Kugeln gezogen werden?
4. Wie groß ist die Wahrscheinlichkeit, dass keine grüne Kugel gezogen wird?
5. Wie groß ist die Wahrscheinlichkeit, dass rote und grüne gezogen werden?
6. Bearbeiten Sie die Aufgabenteile a)- e) für den Fall, dass die Kugeln nicht wieder zurücklegt werden.

kann mir vielleicht jemand bei der Aufgabe behilflich sein?
vielen Dank im Voraus

Bei der langjährigen Überprüfung von Fahrgästen der städtischen Verkehrsbetriebe wurde ermittelt, dass etwa 2% Schwarzfahrer unterwegs sind, davon 75 % männliche. Allerdings wurden insgesamt auch 55% männliche Fahrgäste gezählt. Ein Fahrgast wird überprüft.

a) Mit welcher Wahrscheinlichkeit wird eine Frau mit Fahrschein kontrolliert?

b) Mit welcher Wahrscheinlichkeit wird eine männliche oder eine Person mit Fahrschein kontrolliert

Wie berechne ich das? Ich komme nicht weiter..

Hallo, ich habe hier ein Baumdiagramm vorgegeben (siehe Bild). Ich muss das Baumdiagramm auch ergänzen. Aber wie komme ich auf die Ergebnisse im Baumdiagram bei der gelben, dunkelblauen und schwarzen Kugel?

Kann mir jemand erklären, was ich auf dem Bild falsch gemacht habe?

Ein im Jahr 07 zugelassener Pkw wird zufällig ausgewählt. () Geben Sie die Wahrscheinlichkeit der folgenden Ereignisse an: A: Der Pkw ist ein Elektroauto. B: Der Pkw wurde privat zugelassen und ist kein Elektroauto. (3) Bestimmen Sie die Wahrscheinlichkeit dafür, dass der Pkw ein Elektroauto ist, wenn er gewerblich zugelassen wurde. (6 + 3 + 3 Punkte) Im Folgenden werden die Verkaufszahlen eines großen Autohauses betrachtet, das sich auf den Verkauf von Elektrofahrzeugen spezialisiert hat. Im Vergleich zum Bundesdurchschnitt verkauft dieses Autohaus überdurchschnittlich viele Elektroautos. So ergab die Analyse der Vorjahresverkaufszahlen, dass 7,5 % der verkauften Autos Elektroautos waren. Diese empirisch ermittelte relative Häufigkeit soll im Folgenden als Wahrscheinlichkeit dafür angesehen werden, dass ein verkauftes Auto ein Elektroauto ist. Die Anzahl verkaufter Elektroautos wird im Folgenden als binomialverteilt angenommen. b) () Das Autohaus stellt eine Prognose für die nächsten 000 Autoverkäufe auf. Bestimmen Sie die Wahrscheinlichkeit folgender Ereignisse: E : Es werden genau 80 Elektroautos verkauft. E : Es werden mindestens 70, aber höchstens 80 Elektroautos verkauft. E 3 : Die Anzahl der verkauften Elektroautos entspricht genau dem Erwartungswert. () Ermitteln Sie, wie viele Autos mindestens verkauft werden müssen, damit darunter mit einer Wahrscheinlichkeit von mindestens 90 % mindestens ein Elektroauto ist. 

Bei einem Spiel mit Buchstaben Karten werden die Buchstaben des Wortes SOLO

ungedreht und vermischt.

Es werden 3 Karten hintereinander aufgedeckt und deren Buchstabe jeweils notiert.Nachdem eine Karte gezogen wurde, wird diese zurückgelegt, umgedreht und die Karten vermischt.

1. zeichne das dazugehörige Baumdiagramm
2. wir groß ist die Wahrscheinlichkeit, dass der Reihe nach das Wort LOS entsteht

Guten Mittag,

meine Frage bezieht sich auf die Aufgabe 4 c).

4c)

Berechnet werden soll ja die Anzahl der möglichen Ergebnisse, bei denen die Augenzahlen verschieden sind.

Beim ersten Würfel kann noch jede Zahl drankommen, also gibt es 6 Möglichkeiten. Beim zweiten Würfel können noch 5 Zahlen drankommen. Beim dritten Würfel können noch 4 Zahlen drankommen. Beim vierten Würfel können noch 3 Zahlen drankommen. Beim 5. Würfel können noch 2 Zahlen drankommen.

Also berechne ich:

p = 6 * 5 * 4 * 3 * 2 = 6!/1! = 720 Möglichkeiten.

Wieso steht in der Lösung aber:

p = 6! = 6 * 5 * 4 * 3 * 2 * 1 = 720 Möglichkeiten?

Zwar ist das Ergebnis gleich aber es gibt doch nur 5 Würfel und in der Lösung werden 6 Zahlen multipliziert. Ist der Ansatz in der Lösung richtig?

Bei einem Glücksspiel wird das abgebildete Glücksrad einmal gedreht.

Als Einsatz bezahlt man 3 €.

Man erhält den Betrag der ausgezahlt, der auf dem feld zu sehen ist, welches nach der Drehung oben steht.

Bestimme den erwartungswert.

Eine Rubbelkarte enthält 25 mit einer undurchsichtigen Schicht überzogene Felder, von welchen 10 gewinne und 15 Nieten sind. Daniela rubbelt 2 Felder auf. Mit welcher Wahrscheinlichkeit hat sie genau ein Gewinnfeld aufgerubbelt?

Zwei Glücksräder, deren Einzelsektoren alle gleich groß sind, werden gleichzeitig gedreht. Das eine Glücks-ad hat 2 rote und 4 blaue Felder. Das andere Glücksrad hat 2 rote, 2 grüne und 3 blaue Felder.

Guten Abend,

wieso steht bei c) als Antwort, dass bei b) die Wahrscheinlichkeit steigt, wenn am Wochenende weniger Kinder geboren werden?

Bei b) geht es ja um die Wahrscheinlichkeit für die Geburtstage Dienstag, Donnerstag, Samstag. Wenn nun am Wochenende weniger Kinder geboren werden sinkt doch die Wahrscheinlichkeit für geborene Kinder an Samstagen. Klar nimmt dann die Wahrscheinlichkeit für Dienstage und Donnerstage zu aber wieso steigt hier die Wahrscheinlichkeit? Wie berechnet man das?

Bei einem Brettspiel werden 2 Würfel mit einer gelben, zwei blauen und drei roten Seiten benützt.

es werden 2 Würfel geworfen

E1 - kein Würfel zeigt rot

E2 - ein Würfel zeigt rot

E3- beide Würfel haben die gleiche Farbe

Aufgabe:

Ein Wurf mit zwei Würfeln kostet 1€ Einsatz. Ist das Produkt der beiden Augenzahlen größer als 20, werden 3€ ausbezahlt. Ist das Spiel fair? Wie müsste der Einsatz geändert werden, wenn das Spiel fair sein soll?

Kann mir jemand helfen?

Mein Kopf qualmt und ich weiß nicht wie ich an die gelbmarkierten Werte komme. Könnte mir jemand hier bitte Helfen 😊

Hallo ich komme hier bei einer aufgeb nicht weiter , könnte mir jemand bitte helfen ?
die Aufgabe 7 :

Was ich schon versuchte habe

bei a) muss man die Wahrscheinlichkeit von einem funktionierenden Handy unter der Bedingung dass es überhaupt funktioniert finden

Ich habe mir gedacht , vielleicht muss ich irgendwie durch den Mittelwert rausfinden wie viel es nach einem Jahr ist aber das geht ja nicht weil die Wahrscheinlichkeiten ja nicht immer gleich sind :/

bei b ) muss man die wahrscheinlichlichleut nach 4 Jahren unter der Voraussetzung dass es schon 2 Jahre funktioniert hat finden

also schätze ich mal

P2jahre (4jahre ) aber irgendwie weiß ich nicht was ich dann in die Formel der bedingten Wahrscheinlichkeit reintun soll …

Hallo,

Berechne:

Peter und klaus spielen Tennis.Mit einer Wahrscheinlichkeit von 0,6 gewinnt Peter einen Satz und mit 0,4 Paul. Sieger ist der der zuerst 4 mal gewonnen hat, dann endet das Spiel sofort. Wie hoch ist die Wahrscheinlichkeit das Peter 4:1 gewinnt

4:2,4:3,4:0

Paul gewinnt:

4:0,4:1,4:2,4:3

Von den Lehrkräften eines Landes arbeiten 25% an einem Gymnasium. 15%der Lehrkräfte sind weiblich und arbeiten an einem Gymnasium. Insgesamt sind 72% der Lehrkräfte weiblich. 

a) Stelle den Sachzusammenhang in einer vollständig ausgefüllten Vierfeldertafel dar.  (3 BE)

b) Ermittle die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Lehrkraft weiblich ist oder an einem Gymnasium arbeitet. (2 BE)

c) Eine zufällig ausgewählte Lehrkraft ist weiblich. Bestimme die Wahrscheinlichkeit dafür, dass sie an einem Gymnasium arbeitet. (2 BE)

d) 100 Lehrkräfte werden zufällig ausgewählt. Bestimme die Wahrscheinlichkeit dafür, dass unter diesen 100 Lehrkräften die Anzahl derer, die nicht am Gymnasium arbeiten, mindestens viermal so groß ist, wie die Anzahl derer, die am Gymnasium arbeiten. 

Ich brauche hilfe bei e. Wie finde ich heraus, wie viele von den 100 Lehrkräften an einem Gymnasium arbeiten? Ich müsste diese Zahl mit 4 multiplizieren und dann zumindest die Wahrscheinlichkeit berechnen. Das kann ich, aber ich weiß nicht, wie ich die Zahl von 100 Personen herausfinden soll, die in der Turnhalle arbeiten.

Aufgabe 1

Bestimmen sie für eine binomialverteilte Zufallsgröße mit n = 5 den zweiten Parameter p so, dass gilt



Aufgabe 2

Im Dezember erhalten Blutspender ein kleines Weihnachtspäckchen. Besonders begehrt sind die Päckchen, die Mathe-Knobeleien enthalten. Ermitteln Sie, wie groß der Anteil der Präsente mit Mathe-Knobeleien sein muss, damit sie mit mindestens 90 Prozentiger Wahrscheinlichkeit in mindestens einem von zwanzig Päckchen zu finden sind.

danke im Voraus :)

Hab nach 2 versuchen mit 5 würfeln nen 6er kniffel gewürfelt, beim ersten try warens 2 , beim zweiten die restlichen 3

Hallo schreibe morgen ein Mathearbeit würde gerne eine Frage wissen unzwar wie man die Wahrscheinlichkeit berechnet ,dass etwas KEIN MAL trifft also z.b

Simon schätzt die Wahrscheinlichkeit dafür,dass er beim torwandschießen trifft , auf 70% . Er hat vier versuche. berechne auf Grundlage seiner Schätzung die Wahrscheinlichkeit dafür dass Simon

A keinmal trifft .

B viermal trifft

C mindestens einmal trifft

D daneben schießt

Hallo,

ich habe mal nur eine inhaltliche Farbe. Wie sieht man, welche Würfel eine Rote Seiten haben? Denn ich sehe doch gar nicht alle Würfel und vor allem nicht von allen Seiten.

(das Thema ist bedingte Wahrscheinlichkeit)

Kann jemand diese Aufgabe für mich lösen mit Erklärung bitte. Danke im Voraus

Mira bearbeitet einen Single-Choice-Test mit vier Fragen. Bei jeder Frage gibt es drei Ant-

wortmöglichkeiten, von denen genau eine richtig ist. Da Mira die Antworten nicht weiß,

kreuzt sie bei jeder Frage zufällig eine Antwort an.

Ermittle, mit welcher Wahrscheinlichkeit Mira mindestens eine Frage falsch beantwortet

Kann mir jemand bei den beiden Aufgaben helfen? Bei 6 ist mein Ansatz: Also “49 über 6” hat = 13.983.816 Tipps sind möglich. Für “drei richtige” also aus den 6 über 4 hat man 15 Möglichkeiten und bei 6 über 3 sind es 20 Möglichkeiten… jetzt hängt es aber

Hallo leider habe ich letzte Woche im Matheunterricht gefehlt aufgrund einer Exkursion mit einem Kurs. Ich wiederhole gerade die Aufgaben und komme hier überhaupt nicht weiter, da wir nun bei den Thema bedingte Wahrscheinlichkeit sind. Kann mir jemand erklären, wie man die Aufgabe genau löst?

Die Aufgabe:

Lösungsansatz dazu:

Hallo noch einmal,

wir sollen diese Vierfeldertafel so ausfüllen, dass diese stochastisch unabhängig ist, meine Lösung ist nun aber stochastisch abhängig. Wo liegt mein Fehler?

Aufgabe 2a)

Folgende Aufgabe:

Wie vervollständige ich die Tabelle unter der Voraussetzung, dass die Ereignisse A und B stochastik unabhängig sind?

Weiter als so komme ich nicht:

Bitte dringend um Erklärung :(

Ich habe die Frage letztens gestellt bekommen und zerbreche mir seither den Kopf. Wichtig zu beachten bei dem Beispiel ist, dass es sich um einen regulären Würfel (1-6) handelt der 3 mal hintereinander gewürfelt wird. Die offensichtliche Antwort die man bekommt lautet 3/216. Jetzt stelle ich mir die Frage: Dadurch das 3 Kombinationen in frage kommen (6;6;5/6;5;6/5;6;6) ist die wahrscheinlichkeit beim ersten Wurf die Kriterien zu erfüllen 2/6. Sollte beim ersten Wurf eine 6 erzielt worden sein ist es beim zweiten Wurf abermals 2/6 da man noch entweder eine 5 oder eine 6 Würfen kann. Lediglich bei dem letzten Wurf ist die Wahrscheinlichkeit 1/6 wodurch sich eine Gesamtwahrscheinlichkeit von 5/216 ergibt. Zu bemerken ist, dass sollte es sich beim ersten Wurf um eine 5 handeln die wahrscheinlich lediglich bei 4/216 liegt, da man dann ja beim 2 & 3 Wurd jeweils nur eine Möglichkeit hat. Deswegen frage ich wieso die eindeutige Antwort für viele bei 3/216 liegt…Macht mein Gedankengang doch keinen Sinn?

vg max

Danke im Voraus..

Habe morgen eine Mathearbeit. Danke.

Zwei Würfel mit den abgebildeten Netzen werden geworden. Ich habe jetzt diese Tabelle erstellt. Wie erkenne ich in der Tabelle einen Pasch?

Warum umwandelt mann den prozent in ein dezimalzahl beim Baumdiagramm?

Hallo wir haben in Mathe mit diesem Thema neu angefangen aber unser Lehrer war nicht da und hat es uns als Hausaufgaben gegeben uns es selbst beizubringen. Kann mir jemand vielleicht einen Ansatz für Aufgaben a) geben und etwas dazu erklären damit ich wenigstens weiß wie man das macht? Auf den vorherhigen oder folgenden Seiten gibt es keine Erklärung hierzu. Vielen Dank im vorraus

Hallo, ich habe gerade Schwierigkeiten bei meinen Mathe HA, hier wird gefragt, wie hoch die Wahrscheinlichkeit ist, dass zwei mal hintereinander Gelb angezeigt wird. Ich kam zum Ergebniss "2/6" was aber keinen Sinn ergibt.

" durch eine Befragung will man herausbekommen wie viele Menschen ihre Partner betrügen. Dazu wird folgende zufällige Technik genutzt : die befragte Person wird gebeten, verdeckt einen Würfel zu werfen. Kommt 1-4 so soll sie die Frage ehrlich beantworten, bei 5-6 soll die immer Ja antworten "

Aufgabe : wir sollen zuerst ein Baumdiagramm Zeichen. Das habe ich erledigt. Auf dem einen Ast stehen die Würfelzahlen 1-4 und auf dem anderen Ast die Würfelzahlen 5-6.

Bei den Würfelzahlen 1-4 ist die Wahrscheinlichkeit 4/6, bei den Würfelzahlen 5-6 ist die Wahrscheinlichkeit 2/6

Aufgabe : 45% der Befragten gibt die Antwort "ja". Berechne die Betrügensrate unter den Befragten.

Hier weiß ich leider nicht wie ich vorgehen soll. Kann mir bitte jemand helfen

Ich brauche Hilfe bei einer Mathematiksufgabe

"Eine gezinkte Münze wird 120 mal geworfen. Die Wahrscheinlichkeit für das Ergebnis Zahl beträgt P(Z) =0,45.

Wie oft wird das Ergebnis Wappen erwartet?"

Wie kommt man auf 0,45 und wie berechnet man das Ergebnis für Wappen?

Hey!

Ich habe hier eine Aufgabe bei der ich sehr Probleme habe. Die Aufgaben a) bis c) habe ich schon verstanden. Bei der Aufgabe c) habe ich mir gedacht, die Bedingung der Normierung bei Wahrscheinlichkeiten als Antwort zu nehmen. Bei den anderen Antworten scheiterts. Könnt ihr vielleicht Ansätze nennen? Danke 🥰

Hallo, wir mussten als Hausaufgabe folgende Aufgabe lösen:

"In einer Urne liegen 5 Kugeln mit den Beschriftungen 1, 2, 3, 4, 5. Folgendes Experiment wird viermal durchgeführt: Es wird eine Kugel gezogen, die Nummer notiert, die gezogene Kugel wird wieder in die Urne gelegt."

c) Wie groß ist die Warscheinlichkeit, dass sich die Zahlen 1, 2, 3 und 4 unter den gezogenen Kugeln befinden?

Das Problem ist nun dass ich eine Warscheinlichkeit von 99,84% raushabe aber meine Lehrerin meint, dass 96,16% die richtige Lösung ist. Daher würde ich gerne wissen ob meine Lehrerin wirklich Recht hat und wenn ja wie der richtige Rechenansatz ist.

Könnte mir einer bitte helfen.( Gleichung aufstellen)

1. In einer Urne befinden sich 3 grüne und eine unbekannte Anzahl blauer Kugeln. Es werden zwei Kugeln mit Zurücklegen gezogen. Wie viele blaue Kugeln waren vorhanden, wenn die Wahrscheinlichkeit, dass mindestens eine blaue Kugel gezogen wird, 0,91 beträgt?

Wir haben vorhin mit dem Thema Wahrscheinlichkeitsrechnung bzw. Stochastik angefangen

Ich muss folgende Aufgabe bearbeiten:

ein Würfel wird einmal geworfen. Geben Sie zwei weitere denkbare Ergebnismengen und ihre Mächtigkeit an.

Ich verstehe das nicht ganz. Die Ergebnismengen sind 1,2,3,4,5,6 und Anzahl der Ergebnisse ist doch 1 oder nicht?

Also bei der Wahrscheinlichkeit 1:140.000.000

Wie kann ich jemanden diese Zahl und geringe Wahrscheinlichkeit verdeutlichen und zeigen. Weil wenn man die Zahl so hört denkt man sich, joa das ist machbar. Kennt ihr gute Beispiele?

Verzweifeln gerade an einer Mathe Aufgabe für das Studium bei der Klausurvorbereitung kann uns jemand aushelfen?

Es wird ein Würfel 4 mal nacheinander geworfen b.) Wie groß ist die Wahrscheinlichkeit eine Zahl kleiner als 14 zu würfeln unter der Bedingung dass der dritte Würfel eine 3 ist? 

Hilfe bei c bitte (mindestens 2 Fragen richtig).

Ich lerne grade auf meine Statistik Klauser und habe diese Aufgabe und frage mich ob ich doof bin oder ob ich das so machen darf:

Aufgabe: Kartenspiel mit 32 Karten, es wird 2 mal ohne Zurücklegen gezogen.

Gesucht: Wahrscheinlichkeit mit der bei beidem mal Ziehen ein Ass gezogen wird.

Ich hab also einfach gesagt dass Ereignis A das erste Ass mit Wahrscheinlichkeit 4/32 ist und Ereignis B das zweite Ass mit Wahrscheinlichkeit 3/31 ist.

Weil wir nicht zurücklegen und daher eine Karte weniger insgesamt (32-1) und ein Ass weniger (4-1) nach dem ersten Ziehen vorhanden ist.

Dann einfach P(A ∩ B) = P(A) * P(B) = (4/32)*(3/32) = 1,21%

Das ist dieselbe Lösung wie der Professor mit einer ewig langen Rechnung mit Kombinatorik, Fakultät, bla bla bla hat. Daher frage ich mich, darf ich das so machen, oder denke ich zu einfach? Ist das Ergebnis zufällig gleich?

Hallo liebe Community :)

Ich komme bei folgender Aufgabe nicht weiter... könnt ihr mir vielleicht helfen?

Zu einer Ausstellung in A kamen an einem Tag 1600 Zuschauer, davon 460 direkt aus der Stadt, der Rest von Außerhalb. 840 der Zuschauer von Außerhalb waren Frauen und der Rest Männer und Kinder. Insgesamt waren die Frauen mit 70 % deutlich in der Überzahl.

a) Die 10000ste Besucherin wird besonders interviewt. Berechnen Sie die Wahrscheinlichkeit, dass diese zufällig ausgewählte Frau aus A kommt.

b) Der 5000ste Besucher kommt von Außerhalb. Berechnen Sie die Wahrscheinlichkeit, dass es ein Mann oder ein Kind ist.

Vielen Dank und liebe Grüße

Jessi :)