Vektoren – die neusten Beiträge

Hallo miteinander,

Kann mir bitte jemand helfen die folgende Formel herzuleiten?

Ich dachte zunächst, dass ich den freien Vektor AB mit den Ortsvektoren beschreiben muss, also -a + b + BC, wobei BC ja = c - b wäre?

Hallo,

ich habe heute die Hauptschulprüfung in Mathe geschrieben und vergessen den Rechenweg hinzuschreiben.

Ich habe meine Rechnungen entweder auf den Schmierzettel geschrieben oder direkt in den Taschenrechner eingegeben und dann auf das Reinschriftpapier geschrieben.

Ich habe bei jeder Aufgabe nur die Lösung hingeschriebenen, bekomme ich jetzt Punktabzüge oder werden die Aufgaben nicht gewertet.

(eigentlich schreibe ich immer den Rechenweg hin, nur heute habe ich es irgendwie komplett vergessen weil ich Angst hatte das ich das alles nicht in der Zeit schaffe.)

Danke im Voraus

Angenommen ich habe 3 Vektoren v1, v2 und v3 in R^3 die Linear unabhängig sind. Und ich kann mit den Vektoren einen beliebigen Vektor w durch Linearkombination darstellen. Dan bilden die 3 Vektoren v1, v2 und v3 eine Erzeugendensystem? Wenn aber die 3 Vektoren linear abhängig sind und ich dennoch durch Linear Kombination einen beliebigen Vektor w darstellen kann, sind die Vektoren dann auch ein Erzeugendensystem?

Sie geht doch so, Daumen V, Zeigefinger B, Mittelfinger Fl.

Aber wenn ich das bei der Zeichnung mache, zeigt B aus der Ebene raus und nicht rein. mache ich was falsch?

Zu der Grundfläche ABCD der Pyramide wurde paralle eine Zwischenebene EFGH eingezogen, wobei ihr Mittelpunkt der Punkt N ist, welcher durch die Höhe h verläuft. h geht von M (Mittelpunkt von ABCD) bis S (Spitze der Pyramide). Es gilt Strecke AC=8cm und Strecke NG=3cm. In welcher Höhe von der Grundfläche aus befindet sich die Zwischenebene EFGH und wie hoch ist die Höhe der Pyramide(Strecke MS)?

Wäre sehr dankbar über schnelle Hilfe

es geht um die Aufgabe c). Ich bekomme sie einfach nicht gelöst. Weiß jemand von euch weiter ? Vielen Dank schon mal !

Hey, kann mir jemand bitte bei diesen Aufgaben helfen? Ich halte in einer Woche eine Präsentation darüber, und komme, gar nicht mit dem Thema klar. Kennt jemand die Lösungen und will mir helfen?

Vielen Dank.

Kann mir vielleicht jemand erklären, wie ich das begründen kann, weil ich gerade echt verzweifle, weil ich das nicht verstehe.

Folgende Aufgabe:

 Gegeben sind die Punkte A und B mit den Koordinaten A (3|4|2) und B(8|-11|12) sowie die Gerade g mit der Gleichungg:x=(6,5|-6,5|9)+r•(-7|21|-14)

Das soll natürlich die Parameterform sein, war aber leider nicht besser abzutippen.

1. Geben Sie eine Gleichung der Geraden h an, die durch die Punkte A und B verläuft.
2. Weisen Sie nach, dass der Punkt A auf der Geraden g liegt.
3. Untersuchen Sie die Lage der Geraden g und h zueinander.
4. Geben Sie eine Gleichung einer Geraden an, die die Gerade g im Punkt A schneidet.

Mit den ersten Beiden Aufgaben habe ich keine Probleme, aber wie kann man bei c vorgehen? Danke im Voraus!

Hallo, Ich bin gerade dabei für meine mündliche Mathe Abi Prüfung zu lernen und bin auf diese Aufgabe gestoßen (die Lösung steht drunter). Ich habe bis jetzt alles richtig ausgerechnet, nur das bei mir nicht der Winkel 23,87 rauskommt wenn ich den arccos verwende. Ich kriege nämlich 0,41 raus was eigentlich falsch sein sollte, ich weiß aber nicht wo mein Fehler liegt……

Kann mir jemand helfen?

Danke im Vorraus!

Also ich hab da mal nh frage:

Die großkreise der erde sind ja die Meridiane und der Äquator.

Und wenn ich jetzt zwei städte habe und deren Abstand berechne, dann berechne ich theoretisch den Großkreis, weil das ja die kürzeste Entfernung ist.

Aber ich versteh nicht so ganz, warum man den großkreis berechnet wenn der schon angegeben ist.

ZB San Francisco und Frankfurt haben nen Abstand von 9000km. Aber auf welchem Großkreis liegt der?

Die frage is safe voll unlogisch aber naja :D

Folgende Umformung wurde in der Vorlesung gemacht (Geht vor allem um die erste):

Ich bin nicht so fit in Matrizengleichungen also wollte ich das mal nachrechnen und bin auf folgendes gekommen:

Links ist mein weg, rechts das aus der Lösung. Da sind einfach die Summanden transponiert, aber ich versteh nicht wieso man das darf. Ich denk dann müsste auch der 0-Vektor zurück transponiert werden.

Ich hab mir zur Hilfe mal die Vektoren + Matrix gemalt:

Wenn das nicht falsch ist, wären das in der 2. Zeile der Lösung ja 2 Vektoren der Länge m die subtrahiert werden, dann müsste der 0-Vektor aber nicht transponiert sein, oder?

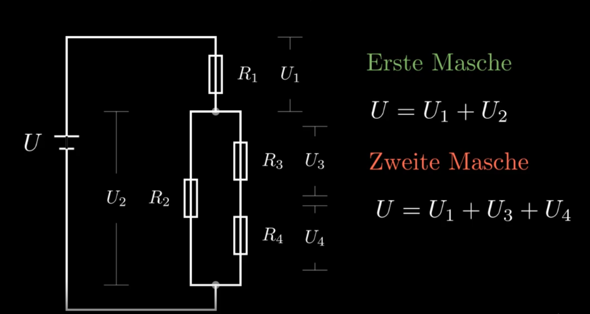
Drei identische Plattenkondensatoren (C1, C2, C3) haben jeweils eine Kapazität von 60 µF. In einen der drei Kondensatoren wird ein Dielektrikum eingesetzt, so dass der Raum zwischen den Platten völlig ausgefullt wird. Hierdurch steigt seine Kapazität auf 95 µF. Jetzt werden die Kondensatoren parallel geschaltet, auf 120 V aufgeladen und dann von der Spannungsquelle getrennt.

a) Wie groß ist die gespeicherte Energie im System?

b) Wie groß sind die Ladungen, welche sich auf den jeweiligen Kondensatoren befinden?

c) Wie groß sind die Ladungen, welche sich auf den jeweiligen Kondensatoren befinden, wenn das Dielektrikum wieder entfernt wird?

d) Wie groß ist die gespeicherte Energie im System nach dem Entfernen des Dielektrikums?

Ansatz

a) E = 1/2 C * U² = 1/2 (60 µF + 60 µF + 95 µF) * 120 ² V = 1,548 J

b) Q1 = Q 2 = C1 * U = 60 µF * 120 V = 7,2 * 10^-3 C.

Q3 = C3 * U = 95 µF * 120 V = 0,0114 C.

c) Hier bin ich mir jetzt nicht sicher. Die Ladung ist wieder gleichverteilt, also ist Q_Ges = Q1 + Q2 * Q3.

Für Q1 und Q2 nimmt man jetzt wieder 7,2 * 10^-3 C. Für Q3 wird in unserem Skript jetzt 0,0114 C vorgeschlagen. Aber ich verstehe das nicht. Das Dieelektrikum wird doch jetzt wieder entfernt. Sollte es dann nicht auch 7,2 * 10^-3 C sein und nicht 0,0114 C?

QGes = Q1 + Q2 + Q3 = 7,2 * 10^-3 C + 7,2 * 10^-3 C + 0,0114 C = 25,8 * 10^-3 C.

QGes = 25,8*10^-3 / 3 = 8,6 * 10^-3

d) E= 1/2 * C * U²

Da Q = C * U => U = Q/C

=> E = 1/2 * C* (Q/C)² = 1/2 * Q²/C

=> El = 1/2 ( (Q1 + Q2 + Q3)/(C1 + C2 + C3))²

= 1/2 ((25,8*10-3 C)/ 60 µF+ 60 µF + 60 µF.)² = 1,849 J.

Ich verstehe es nicht.

Warum wird in der Teilaufgabe c), wo die Ladung nach Entfernen des Diektrikum berechnet werde sollen mit den Wert von 95 µF weitergerechnet und bei der d), wo die Energie im System nach Entfernen das Dieelektrikums berechnet werden soll wieder nur 60 µF?

Also konkret:
Warum rechnet man bei c) QGes = Q1 + Q2 + Q3 = 7,2 * 10^-3 C + 7,2 * 10^-3 C + 0,0114 C = 25,8 * 10^-3 C. und nicht QGes = Q1 + Q2 + Q3 = 3 * 7,2 * 10^-3 C ?

Und wieso rechnet man bei der d) dann plötzlich wieder 1/2 ((25,8*10-3 C)/ 60 µF+ 60 µF + 60 µF.)² statt 1/2 ((25,8*10-3 C)/ 60 µF+ 60 µF + 95 µF.)²

Das erscheint mir doch sehr inkonsistent, dass man bei der c) nochmal die 95 µF hat und bei der d) plötzlich nur noch die 60µF

Liebe Grüße,

euer sehr verwirrter Jensek81

Ich sitze seid 2h an der Aufgabe und verstehe wenig :(

ist jmd in der Lage diese zu bearbeiten ?
danke im Voraus für eure Unterstützung

Berechnen Sie den Flächeninhalt des Dreieckes ABC. Kann ich dies auch ohne das Kreuzprodukt rechnen?

a) A(1,1,1) ; B(7,4,7) ; C(5,6,-1)

hallo, ich muss die aufgäbe unten rechnerisch lösen. ich weiss dass ich ein Kräfteparallelogramm machen muss aber ich weiss nicht wie. vor allem verstehe ich nicht, wie ich den Maßstab machen muss. ich dachte an 6cm für die 12kg, aber was soll ich denn dann mit den Metern machen? Kann mir bitte jemand helfen ich sitze echt ewig daran

Mein Problem ist, dass Ich nicht weiß wie ich vorgehen soll bei dieser Aufgabe und was ich als Lösung rausbekommen soll. Ich habe schon mein Leher gefragt, aber er halt mir nicht weitergeholfen. Gibt es hier einer der es mir gut erklären kann und die Lösungsweg zeigen kann, damit ich es besser verstehen kann?

Die Aufgabe lautet:

In Figur 1 und Figur 2 sind die rot eingezeichneten Punkte jeweils Mittelpunkte einer Seitenfläche bzw. einer Kante. Bestimmen Sie eine Parametergleichung für jede eingezeichnete Gerade

a) im Quader in Fig, b) in der quadratischen Pyramide Fig.2

Da keine Punkte angegeben sind, wodurch meine Gerade verlaufen soll darf ich einfach den Ortsvektor von E übernehmen? Und wie machen ich das danach mit dem Skalarprodukt?

Hallo,

ich lerne aktuell Mathe und habe es mit zwei Formeln zu tun, die ich nicht unterscheiden kann (siehe Foto).

Die eine ist wohl dazu da um den Winkel zwischen zwei Vektoren zu berechnen, die andere um den Schnittwinke zwischen Geraden zu bestimmen.

Wo liegt da nun der Unterschied? Ein Vektor ist doch auch eine Gerade oder nicht?

Kann mir das jemand erklären?

Warum wird hier z.B. negative Winkel nicht ausgeschlossen (oder welche über 360°) ?

Ich meine, ich kann ja auch keine negativen Winkel zeichnen....

Es geht eigentlich nur um das rote, wo für E die Formel eingesetzt wird. Meine Frage, die Formel nimmt man doch normalerweise mal den Einheitsvektor von r, wenn man auch die Richtung des Vektors sucht (Q/(e4pie0*r^2))*(r/|r|).

1. Wieso macht man das hier nicht? Ich meine, es steht da, dass es nicht nur um den Betrag von E geht, sondern um den Vektor E. Genauso bei A.
2. Aber beim 2. Schritt fällt das Flussintegral weg, geht es ab da nicht mehr um die Vektoren, sondern A und E als ganzes?

Hier geht es um einen el. Fluss durch eine Fläche. Das heißt doch, man unterteilt die Fläche A in unendlich kleine unendlich viele Flächenelemente dA. Aber wenn die Länge des Vektors den Betrag der Fläche dA bedeutet, wie soll das gehen, wenn die Fläche von dA unendlich klein ist?

Hallo,

ich hab heute zum ersten Mal LGS lösen verstanden und hab mich dann an paar Aufgaben gewagt. Jedoch ist mir bei diesem LGS bei y=-7 ein Fehler passiert, den ich irgendwie nicht aufdecken kann.

Ich weiß nicht, wo ich den Fehler gemacht habe, vielleicht erkennt ihn ja jemand?

Jedenfalls steht in den Lösungen für y=3

Bestimmen sie a) den ersatzwiderstand der schaltung bild 4, b) den strom durch R4 und c) die gesamtstromstärke

Hallo allerseits. Ich stehe gerade ein klein wenig auf dem Schlauch. Und zwar suche ich nach einer Möglichkeit, zu einer Menge V, von der man weiß, dass es sich um einen endlich erzeugten Vektorraum handelt, eine Basis zu bestimmen.

Wenn V nun eine Menge ist, die man sich halbwegs "vorstellen kann", erkennt man ja häufig, wie eine Basis aussehen könnte und muss dann nur noch beweisen, dass es tatsächlich eine ist (z.B. über lineare Unabhängigkeit und das Erzeugendensystem).

Was mache ich aber nun, wenn ich mir die Menge V einfach nicht so richtig vorstellen kann und es mir deshalb nicht gelingt, mir eine Basis auszudenken. Vielleicht kenne ich ja noch nichtmal die Dimension des Vektorraums und weiß nichtmal, wieviel Basisvektoren ich eigentlich suche? Gibt es dann ein bestimmtes Vorgehen, dass mich direkt zu einer Basis bringt?

Meine beste Idee wäre es jetzt gewesen, ein paar Vektoren aus V zu nehmen und zu prüfen, ob sie ein Erzeugendensystem bilden. Wenn dem nicht so ist, ergänzen ich immer weiter mit zufälligen Vektoren aus V und hoffe, dass ich irgendwann eine Teilmenge von V habe, die ein Erzeugendensystem vom V bildet. Anschließend würde ich dann solange linear abhängige Vektoren aus der Menge streichen, bis ich eine linear unabhängige Teilmenge von V habe. Das wäre dann meine Basis. Wenn V nun aber eine echt komplizierte Menge ist und vielleicht eine hohe Dimension hat, ist diese Herangehensweise aber doch sehr ineffizient. Deshalb suche ich nach eine Verfahren, um möglichst direkt eine Basis bestimmen zu können.

Ich würde mich sehr darüber freuen, wenn mir jemand weiterhelfen könnte.

8 c.

ich habe es versucht, könnte mal jemand bitte drüber schauen,evt. ergänzen🙏🏼

Hello :) kann mir jemand vllt helfen den richtigen Ansatz zu finden für diese Aufgabe ? Ich verzweifel grade an der Aufgabe und habe mir die Formelsammlung angeschaut, schaffe es aber nicht diese Textaufgabe in die richtigen Formeln umzuformen! Vllt kann mir hier jemand sagen, wie man dabei vorgehen muss.

Unsere Übungen mit denen wir den schiefen Wurf angefangen haben, waren anders aufgebaut.

Vielen Dank !

Bitte kann jemand aufgabe 7 lösen? ich bekomme es echt nicht hin. also mit rechenweg wäre super super🙏💞

Könnte mir jemand helfen und a) und c) machen? ich hab es auch selbst gemacht aber bei mir kam ein Ergebnis raus was kein Simm macht. Wäre nett wenn mir jemand helfen könnte. Liebe Grüße

In der Figur sind die Punkte A, B und C die Diagonalenschnittpunkte der jeweiligen Seitenflächen des Quaders. Schneiden sich die Geraden g und h ?

Ich muss für eine Hausaufgabe den Schnittpunkt einer geraden mit der xy bzw yz Ebene berechnen. Mein Ansatz war jetzt, für die Ebenen die Koordinaten Form zu berechnen, allerdings würde da schlussendlich immer nur 0 = 0 rauskommen. Was mache ich falsch?

Eine Airline möchte eine neue Flugroute anbieten. Zuvor muss sie diese allerdings bei Ihnen genehmigen lassen, denn Sie arbeiten bei einer Flugsicherungsgesellschaft im Bereich Planung und Koordinierung der Vorgänge im Luftraum. Ein anderes Flugzeug durchfliegt zeitgleich bereits den von Ihnen überwachten Luftraum gerad-linig. Seine Flugbahn ist durch die Geradengleichung g:x=(-4 8 7) + r (-4 4 2) gegeben. Hinweis: Der Luftraum wird durch ein dreidimensionales Koordinatensystem darge-stellt, wobei eine Längeneinheit 1000 km entspricht.) Damit die neue Route genehmigt werden kann, darf kein Punkt der neuen Route mit der bereits vorhandenen Route übereinstimmen. Die geplante Route verläuft entlang der Geraden h mit der Gleichung h: vektor von x = (1 4 3) + ( -1 2 -1)

Erteilen Sie der Fluggesellschaft die Genehmigung für die geplante Flugstrecke?Begründen Sie. So können Sie vorgehen

1. Suchen Sie gemeinsame Punkte der beiden Geraden. Also Punkte, deren Ortsvek-toren sowohl die Gleichung der Geraden g als auch die der Geraden h erfüllen. Diese Punkte finden Sie, indem Sie die beiden Geradengleichungen gleichsetzen. Achtung! Beim Gleichsetzen müssen Sie darauf achten, dass nicht in beiden Gleichungen der Parameter „r“ heißt. Benennen Sie einfach einen der beiden Para-meter mit dem Buchstaben „s“.

2. Durch das Gleichsetzen erhalten Sie ein lineares Gleichungssystem mit drei Glei-chungen und zwei Unbekannten (r und s), das nun zu lösen ist.

und zuletzt Berechnen Sie nun die Spurpunkte der beiden Geraden. Mit dem beigelegten Bastel-bogen und zwei Fäden lassen sich die durch die Geraden beschriebenen Flugrouten geschickt visualisieren.

Hallo, ich habe leider bei der 2) der folgenden Aufgabe ein paar Probleme...

1) habe ich lösen können. Ich habe die gegebene Gleichung raus, und hatte dazu auch als Nullstellen die -5 und die 5 ausrechnen können. Bei der 2) steht in den Lösungen das Punkt R bei (-5/-49) liegt. Aber wie kommt darauf, das Punkt R auf -5 liegt? Welche Möglichkeiten hat man, um darauf zu kommen? Hat das was damit zutun, das es eine der Nullstellen ist?

Wäre sehr dankbar wenn jemand helfen könnte.

MfG

Hallo,

Ich bekomme diese matheaufgabe einfach nicht hin. Kann mir jemand helfen?

Danke für alle Antworten

Ich bin zwar schon der Auffassung, dass es da zwischen Mond und Erde, einen Zwischenraum gibt.

Aber ich habe ein Problem damit, dass das, aus nichts bestehen soll.

Wenn das so stimmt, was behauptet wird, dass Raum, aus nichts bestehen kann, was ist dann eigentlich der Beweis, dass es den Raum gibt?

Es besteht ja aus nichts, da kann man ja nicht meinen, dass es etwas ist.

Zeichnet man, auf ein Papier, ein Viereck und in das Viereck, setzt man einen Punkt, ist das, was zwischen dem Punkt und Viereck sich befindet, der Raum.

Aber das Ganze ist ja auf dem Papier und der Raum, kann nur sein, weil es das Papier erlaubt.

Was ist dann das, was das Papier darstellt, mit dem Viereck und Punkt Ding, was bei unserem Universum, diese Aufgabe übernimmt?

Danke schon mal für die Antworten :)

Hallo!

Bei meiner Hausaufgabe kam folgende Aufgabe

Alle andren Aufgaben haben sofort geklappt, nur hier finde ich gar keinen Ansatz. Was wäre bspw. mit V=R2 dann wäre R2xR2 doch einfach wieder R2 ofer nicht? Ich verstehe die Aufgabe null könnte mir jemand eventuell einen Ansatz geben? Vielen Dank fürs Lesen <3

Die Schnittpunkte der Geraden g, h und i sind die Eckpunkte eines Dreiecks ABC. Berechnen Sie die Koordinaten von A, B und C und ermitteln sie den Umfang des Dreiecks.

Ich stehe echt auf dem Schlauch, kann mir jemand bei dieser Aufgabe helfen?

Was bedeuten die Klammern und wie hätte ich es richtig rechnen müssen ?

LG und Danke im Voraus

Von einem rechtwinkligen Dreieck ABC kennt man je zwei Größen. Berechnen Sie die fehlenden vier Größen. a) h=4;q=5 b) p=1;q=2 c) a=5;b=3

a) h=4 und q=5: b=2, c=√41b) p=1 und q=2: a=√2 und c=√3c) a=5 und b=3: c= √34 und h=15√34/34

danke im Voraus!

Habe ich die Aufgabe a, und b) richtig gelöst? Kann jemand der sich auskennt kurz drüber gucken? Und ist meine Schreibweise richtig oder sollte ich iwas anders schreiben?

Okay, ich versuche es mal zusammenzusammenzufassen. Um ein el Feld mit mehreren Ladungen auszurechnen, kann man es einmal simpel zusammenrechnen mit den jeweiligen Qs und Rs (R ist der Ortsvbektor von Q). Und als andere Möglichkeit gibt es die Formel Q= Ladungsdichte*V (parallel zu m=rho*V), und für das Volumen muss man r nach die 3 Koordinaten integrieren oder ableiten? Dementsprechend wird Q ganz unten mit "Volumenintegral nach d^3r von Ladungsdichtefunktion" ersetzt. Meine Fragen:

1. Ich verstehe das mit dem Volumenintegral nicht ganz. Es geht ja darum, dass in einem Volumen eine Ladung ist und die Ladungsdichte überall anders ist. Dementsprechend kann man nicht gleich nach dem ganzen Volumen gehen, sondern integrieren, um Q nur an dem speziellen Punkt auszurechnen, weil es an jedem Punkt anders ist... oder? Mich macht es stutzig, dass ich etwas verstanden habe, weil meistens ist es dann falsch.
2. Wie kann man die rechnerische Vorgehensweise mit diesem Volumenintegral erklären? Ich kann die praktische Erklärung irgendwie nicht mit der Rechnung verbinden.
3. Wie funktioniert diese rechnerische Vorgehensweise? Jeder sagt was anderes. Muss man das Volumenintegral von d^3r*p(r) nehmen? Oder das Volumenintegral über d^3r nach p(r), oder anders?
4. was ist diese Ladungsdichtefunktion überhaupt? Muss da nicht eine Formel sein, um es integrieren zu können?`Auf Google habe ich aber nirgendwo eine gefunden.
5. was bedeutet das dxdydz=d^3r? Was ist hier mit r gemeint? Ich meine eine Seitenlänge gibt es hier nicht... Oder? Und wie rechnet man es aus? Heißt das, man nimmt die Ableitung von Vektor r nach den Koordinaten?

Das waren alle Fragen. Ich bin aber auch schon dankbar, wenn ihr nur eine beantworten könnt.

Bei der folgenden Aufgabe habe ich die Lagebeziehungen berechnet und festgestellt, dass der Richtungsvektor der zweiten Geraden kein Vielfaches der ersten Geraden ist. Somit folgt dass die Geraden jetzt entweder windschief oder schneidend sind. Nach dem Gleichstellen der Geraden und lösen des Linearen Gleichungssystems habe ich festgestellt, dass es einen Schnittpunkt bei L={(6/8)} gibt. Sagt dass jetzt aus, dass sie sich schneiden?

die Aufgabe lautet ja gibt es eine Kollision. Nach Überprüfung mit der Musterlösung habe ich herausgefunden, dass dieser Punkt zwar zeigt, dass sich die beiden Geraden in einem Punkt treffen, aber zu unterschiedlichen Zeiten.

Jetzt versteh ich das nicht wirklich und weiß auch nicht für andere Aufgaben, ob der Schnittpunkt nun dafür steht dass die Geraden sich schneiden? Und woher weiß ich dass sie sich zu unterschiedlichen Zeiten schneiden?

ich freue mich über jede Hilfe:)

Sprich wenn das Ergebnis ungleich 0 ist.

Guten Abend Mathematiker,

ich habe eine Frage zu einer Aufgabe.

Folgendes Szenario:

Ein Heißluftballon bewegt sich konstant pro Sekunde um den Vektor v = (1,2 | -1,8 | 0,5) vorwärts.
Es gibt die Punkte P0 (232|98|159) und P2 (376|-118|219). Der Heißluftballon startet bei P0 und ist nach zwei Minuten bei P2.
Ich muss überprüfen, ob der Ballon den Punkt Q(340|-80|204) auf dem Weg von P0 und P2 passiert.

Die Lösung ist nein, der Ballon passiert nicht Q.
Jetzt zur Frage: Ich brauche die Geradengleichung für die Aufgabe. Ich habe zwei Vorschläge und weiß nicht ob und welches richtig ist.

1. g: x = (232|98|159) + r * (1,2|1,8|0,5)
2. g: x = (232|98|159) + r * (376|—118|219)

Ich weiß, dass es jetzt ein etwas langer Text geworden ist. Ich bitte aber um eine Antwort, falls jemand eine Ahnung hat.
Vielen Dank!

Frage steht oben…

also die Parameterform ist allgemein, um die Ebene oder Gerade darzustellen.

wozu die anderen zwei?

So, jetzt hier, "Physik 2", oder was? Draußen warm, innen kalt. Was heißt das? Naja gut, zunächst erstmal gar nichts. Folgende Aufgabe gilt es zu lösen

Ansatz

Ich weiß dass r_1,2 dasselbe ist wie r_2 - r_1 und | r | dasselbe wie die Wurzel aus r_x² + r_y². Also erstmal die Formel umschreiben. Dann steht da:

So weit, so (un-)gut. Aber jetzt geht die Action los.

1/4π E_0 ist 1/ 4 π * 8,85 * 10^-12 = 8991804694.

Jetzt zum zweiten Bruch: Erstmal der Nenner. Das wäre getreu dem Motto von Pipi Langstrumpf Q1 * Q2 = 3e * 3e. Ein "e" ist 1,6*10^-9. Also 3 * 1,6*10^-19 * 3 * 1,6*10^-19 = 2,304 * 10^-37

So, jetzt zum Nenner. Der Nenner wäre r_2 minus r_1 zum Quadrat. Ich weiß dasss ich Vektoren voneinander substrahiere, indem ich die Komponentenquadrate substrahiere, also jeweils (-3) - 3 rechne. Kommt -6 bei raus. Dann ist der neue Vektor (-6,-6). Davon jetzt den Betrag wäre die Wurzel aus (-6)² + (-6)² = 6√2 und das dann hoch 2 wäre 72. Also wäre der zweite Bruch nichts anderes als 2,304 * 10^-37 geteilt durch 72

So, jetzt zum dritten Bruch. Da steht jetzt oben im Nenner: r2 - r1. Das wäre ja dann wieder der Vektor (-6,-6). Aber das ist doch ein Vektor! Wie soll ich denn einen Vektor in einem Bruch unterbringen? Außerdem steht doch im Nenner dasselbe wie im Zähler, nur als Betrag. Wenn ich eine Sache durch sich selbst teile, kommt doch dann immer "1" bei raus. Wozu dann der ganze Zauber? Und was ist mit F_2,1 gemeint? Wenn ich die Formel rechne, kommt doch dann ein Zahlenwert raus und kein Vektor. Wie soll man das im Koordinatensystem einzeichnen?

Je suis verwirrté

Bei der Ebenengleichung ist es ja möglich, die Parameterform in die Koordinatenform umzuwandeln. Geht das auch andersherum?

Ich bräuchte nämlich für eine Aufgabe die beiden Richtungsvektoren der Ebene, habe aber nur die Koordinatenform vorliegen…

Guten Abend,

Ich sitze an einer Matheaufgabe und weiß gerade nicht weiter,daher bitte ich um Hilfe

Ich wäre für jede Hilfe dankbar.

In der Abbildung seht ihr eine Figur, welche die Grundfläche einer Pyramide darstellen soll. Bei Aufgabe a muss ich rechnerisch prüfen ob es sich hierbei um ein Quadrat oder ein Rechteck handelt. Mein erster Gedanke war, dass ich das Skalarprodukt bilden muss. Wenn das Ergebnis immer 0 ist, dann handelt es sich doch um ein Quadrat oder? Allerdings glaube ich dass ich Fehler in meiner Rechnung eingebaut habe bzw dass es komplett falsch ist (siehe Bild). Außerdem steht da ich soll den Flächeninhalt davon bestimmen. Ich weiß nicht wie ich da vorgehen soll. Bitte helfen 😶

Hi, erstmal dir Aufgabe:

In einem mathematischen Modell wird im Punkt A(1/-3/0) senkrecht zum Erdboden ein 10 Meter hoher Fahnenmast errichtet. Der Erdboden befindet sich in der x-y Ebene, wobei eine längeneinheit einen Meter entspricht. Die Koordinaten des Schattenpunktes S der Mastspitze auf dem Boden zu einem bestimmten Zeitpunkt lautetS(9/3/0). Ermittel einen vektor, der die Richtung der Sonnenstrahlen beschreibt?

Weiß leider nicht weiter. Bitte um Hilfe danke.

Hallo

Ich hätte eine Frage, wieso berechnet man da b=r*c, um zu schauen ob es linear abhängig ist oder nicht. Was ist mit dem vektor a😊

was bringt mir : (1,k)

Hat einer eine Ahnung, wie man hier auf Teil a) kommt?

Hallo,

Ich bin ziemlich verzweifelt an der folgenden Aufgabe, die wir im 2. Semester in Linearer Algebra bekommen haben.

Konkret verstehe ich von Grundauf nicht, was ein Freier Vektorraum ist, dazu habe ich auch im Internet nichts gefunden.

Aber zum anderen wüsste ich auch nicht, wie ich die Aufgabe lösen soll.

Über Hilfe wäre ich sehr dankbar!

Hi,

Ich habe die Aufgabe 1 berechnet. Mit dem GTR (casiofx cg 20)und habe dort eingegeben: Normcd(0,179,8,170) da kam ungefähr 0,8697 raus.

In den Lösungen online kommt aber 0.89 raus...weiß jemand wo der Fehler liegt?

Überprüfen sie, ob die gleichungen dieselbe gerade beschreiben.

Wie kann ich das überprüfen, kann mir das jemand an meinem Beispiel zeigen?

Moin,

In einer Aufgabenstellung stand das eine Ebene mit x3=3 beschrieben wird aber wie soll das gehen, weil eine Ebene braucht doch immer einen Richtungsvektor usw. Wie kann ich mir eine Ebene vorstellen die beschrieben wird durch x3=3?

Warum verläuft die Gerade parallel zur z Achse?

An alle Mathematiker:

was muss gelten für die Parameter r und s damit ein Punkt der Ebene auf dem Rechteck liegt? kann r bzw s auch jeweils 1 sein? Wieso oder

wieso nicht?

Hätte jemand Tipps? Vielen vielen Dank im Voraus. Liebe Grüße und einen schönen Tag euch!

ganz liebe grüße!

souli

Eine Frage, die vor allem an die Fragesteller gerichtet ist:

Wenn Antworten nicht als "hilfreich" bewertet werden oder ganz ohne Reaktion bleiben, dann fragt man sich, woran das liegen mag. Hat man die Erwartungen des Fragestellers nicht erfüllt? Stellt sich die Frage, wie die Erwartung aussehen könnte, wobei mir folgende Optionen in den Sinn gekommen sind:

• "Ich würde die Aufgabe gerne komplett selbst lösen, stecke aber in einem Punkt fest und brauche einen Denkanstoss."
• "Ich möchte ein bisschen Eigenleistung für einen Lerneffekt investieren und wünsche mir daher nur eine Lösungsskizze mit den wesentlichen Schritten."
• "Irgendwie müssen meine Aufgaben, die mich überhaupt nicht interessieren, ja gemacht werden, daher brauche ich eine pfannenfertige Lösung, die nur noch kopiert und abgegeben werden muss ("Hausaufgaben-Service")".

Wie seht ihr das aus Sicht Fragesteller im Bereich Mathematik?

Die Pyramide ist 8m hoch und hat eine quadratische Grundfläche von 44cm.
Wie rechne ich den Neigungswinkel einer Kante zur diagonalen am Boden ?
und wie viel mhoch3 ist nötig es aufzuschütten

Könnt ihr mir bei der Aufgabe bitte helfen ?

Es ist a=(3/0/2) gegeben und b=(-4/2/z)

wie rechnet man es so aus das der Winkel 90grad ergibt ? Bitte hilft mir sehr wichtig

Hallo, ich bin mir unsicher, wie man Ebenen/ Geraden auf orthogonalität prüft und hab da ein paar Fragen.

1.Wann sind zwei Ebenen zueinander orthogonal und wie prüft man das?

2.Wann ist eine Gerade orthogonal zu einer Ebene und wie prüft man das?

3.Wann sind zwei Geraden orthogonal zueinander und wie prüft man das? (beide Richtungsvektoren werden doch zeilenweise multipliziert und wenn da 0 rauskommt sind sie orthogonal, oder?)

Bitte helft mir, ich bedanke mich schon mal im voraus!

Hallo, ich weiß, dass man eine Normalgleichung in eine Koordinatengleichung (KG) umwandeln kann, aber gibt es noch andere Methoden eine KG zu bestimmen? Danke im voraus

Prüfen Sie, ob die Punkte A bzw. B auf der Geraden g liegen, und geben Sie ggf. den Wert des zugehörigen Parameters an.a)

g: vec x = [[2], [- 1], [0]] + t * [[0], [2], [1]] ,

A(2/1/1), B(2|3|1)

Wie gehe ich vor? Kann mir das jemand an meinem Beispiel zeigen?

Normalerweise muss man den Verbindungsvektor zwischen den beiden Stützvektor als zweiter Richtungsvektor der Ebene wählen. Darf man aber auch den den Stützvektor mit dem Richtungsvektor der anderen Gerade verbinden und diesen dann als zweiten Richtungsvektor der Ebene verwenden?

g:x=p+r*v

s:x=d+t*u

Normalerweise: E:x=p+r*v+n*(d-p)

Geht aber auch?:E:x=p+r*v+n*(u-p)

Hallo und zwar hab ich als Hausaufgabe die Nr 13 komplett zu machen. Ich habe bisher nur a und b gemacht. Ich habe versucht die C jetzt zu machen, schaffe es aber nicht bzw. Weiß nicht wie ich sie lösen soll, da nun 3. Funktionen gegeben sind.

Ich benötige Hilfe und danke im Voraus.

Hallo,

ich schreibe morgen meine MatheLK Arbeit und brauche dringend Hilfe!

Ich soll bei einem schiefen Prisma, eine orthogonalen Vektor berechnen, aber wie ??
Ich habe versucht die Strecke AC auszurechnen und diesen Vektor X zu nennen, aber leider stimmt es nicht überein mit den Lösungen. Hier einmal die Aufgabe:

Es ist nur die e)

Ich danke euch für eure Antworten!🙏🏼

Hi, sind Polynome vom Grad >3 ein Untervektorraum?

Gibt es da eine besondere Regel, da man immer wieder davon ließt, dass nur Polynome vom Grad kleiner gleich 3 einen Untervektorraum haben

Kann man, ohne die Eigenvektoren zu berechnen, sagen, ob die Matrix diagonalisierbar ist?

Hi, meine Frage bezieht sich Auf Untervektoren: Hat (x1, x2, x3) ∈ R3: x2 ≤ x1 + x3 einen Untervektorraum?

Die 3 Bedingungen habe ich nachgerechnet und es scheint so, als ob es einen Unterraumvektor hat. Jedoch kommt mir etwas Zweifel auf, da ich zu vermuten meine, dass man immer schreiben kann: x2+y2≤(x1+y1)+(x3+y3). Liege ich da falsch?

Also meine Vermutung bezieht sich darauf, dass wir immer die Form x+y = (x1+y1,x2+y2,...) bekommen können. Kann mich da jemand mit einem Gegenbeispiel korrigieren?

Danke

Hey,

Kann mir jemand die Aufgaben 2a & 2b erklären beziehungsweise lösen?

Ich denke b könnte man zwar googlen aber ein Lösungsweg oder so wäre mir hier lieber.

Vielen dank im Voraus!

Schönen Tag noch

King Schnitzel

Aufgabe: Beschreiben Sie die Lage der Ebene E im Koordinatensystem. E ist hierbei in Parameterform gegeben. Wie gehe ich da vor? Eine kurze Beschreibung der Vorgehensweise würde ausreichen.

Hi, meine Frage bezieht sich Auf Untervektoren: Hat (x1, x2, x3, x4) ∈ R3: x2 = 2*x1 + x3 + x4 einen Untervektorraum?

Weiß jemand die Antwort darauf und kann vielleicht auch erklären, wie man das selber nachrechnen kann?

Ich weiß, dass es die 3 Bedingungen gibt und dass die erste, als dass der Nullvektor in der Menge enthalten ist, erfüllt ist. Wie rechnet man jedoch die Additions und Multiplikations - Bedingungen nach, ohne konkrete Zahlen einzusetzten?

Danke

Hallo, ich bekomme leider diese Aufgabe nicht hin. Es gibt zwei Punkte in dem Koordinatensystem. Diese sind A(2/2/2) und B (3/4/2). Diese bilden den Vektor AB, der die Seite eines Quadrats sein soll. Der Vektor AB ist parallel zur xy-Ebene.

Ich habe den Vektor AB berechnet und komme auf ( 1/2/0). Weiß aber nicht, wie ich jetzt nun vorgehen soll.

Ich kenne die entsprechenden Formeln, also inkl. Nabla und Vektorprodukt, aber bei der tatsächlichen Bedeutung der Rotation im Dreidimensionalen hänge ich - die Rotations"achse" ist ja im Zweidimensionalen die z-Achse, dementsprechend müsste die Rotation im Dreidimensionalen die Existenz einer neue Dimension bedingen (was dann natürlich zeichnerisch nicht mehr darstellbar ist), oder nicht?

Danke im Voraus schon für die Hilfe!

Das obere Bild macht Sinn, also dass die Regel besagt, dass das gesamt U die Summe der U's ist. Aber warte, geht man da nur von der rechten Seite aus oder wieso nur z.B. U1+U2?

Das untere hingegen steht im Skript. Das heißt dann, alle Wieso sind dann alle Spannungen gleich 0? Und wieso muss man da Betrag(U0) dazuzählen?

kann mir jemand die aufgabe 20 erklären?

Ein Auto der Masse 𝑚1 = 10 kg liegt auf einem schrägen Dach (schiefe Ebene) und sei über ein leichtes Seil mit einem Massestück 𝑚2= 4 𝑘𝑔 verbunden.

Der Neigungswinkel des Daches ist 𝛼 = 40°.

Wie groß muss die Haftreibungszahl 𝜇𝑅,ℎ mindestens sein, damit das Auto ruht?

Hallo,

kann mir jemand helfen diese Lineare Gleichungssystem zu lösen? Die Aufgabe ist es, alle Vektoren zu bestimmen, die zu Vektor a und Vektor b orthogonal sind.

ich stehe etwas auf dem Schlauch, da ich nicht weiß wie ich vorgehen muss. Muss ich für eine gesuchte Koordinate eine beliebige Zahl einsetzen oder Additions-/Subtraktionsverfahren anwenden? Und wann ja welches?

danke euch im Voraus:)

Ein Raum ist 10 Meter lang.

In der Mitte ist eine Lichtquelle,
an den gegenüberliegenden Wänden jeweils ein Schirm.
Zwei Uhren mit der gleichen Uhrzeit werden an die Wände angebracht, sie sollen die Uhrzeit messen wenn Licht auf das Schirm trifft.
Beobachter 1 befindet sich außerhalb des Raumes auf der Erde,
Beobachter 2 steht im Raum neben der Lichtquelle.
Vor der Relativbewegung sind für beide Beobachter x1 und x2 gleich lang,
und Uhr 1 und Uhr 2 zeigen die gleiche Uhrzeit an.
Der Raum beschleunigt in die Richtung wie im Bild zu sehen, bis er eine konstante Geschwindigkeit v erreicht.
Die Lichtquelle wird dann eingeschaltet.

Im Inertialsystem von Beobachter 1 müssten beide Uhren die gleiche Uhrzeit anzeigen, und x1 und x2 gleich lang sein. Das Licht trifft zuerst Schirm 1 dann Schirm 2, es legt eine längere Strecke zum Schirm 2 zurück und braucht länger.
Das heißt Uhr 1 zeigt eine frühere Ankunftszeit des Lichts an.


Im Inertialsystem von Beobachter 2 braucht das Licht die gleiche Strecke und Zeit zu beiden Schirmen, da Licht in jedem Bezugssystem die gleiche Geschwindigkeit hat.

Das steht aber im Widerspruch zu den Messergebnissen aus dem anderen Inertialsystem.


Wie sieht das im Inertialsystem von diesem Beobachter 2 aus?
Die Uhren gehen entweder anders oder x1 und x2 sind nicht gleich lang
x1<x2 / t1>t2 ?

Hallo,

ich lerne gerade für meine MatheLK Arbeit über Vektoren und komme nicht weiter.

Ich habe die Pyramide so skizziert:

Ich verstehe nicht warum a + AS den nullvektor ergibt (laut Lösungen)?

Kann mir bitte einer weiterhelfen, auch bei den nachfolgenden Aufgaben?

Vielen Dank!

Hallo, könnt ihr mir bitte helfen und zu erklären wie Mann diese Aufgabe löst und auch versteht.

Wir hatten es und er Schule gehabt, aber ich habe es gar nichts verstanden, wie man diese Aufgabe lösen soll. Der Lehrer hat zwar vieles geschrieben aber ich habe trotzdem nichts verstanden.

Wir schreiben nämlich nächste Woche eine Klausur und uns wurde gesagt, dass es alles von Stoff drankommen wird.

Hallo, kann mir jemand bei Aufgabe 5DF & G helfen und zwar weiß ich das nicht wie ich das mit Abstand machen soll und mit dem Schnnittpunkt.

Beim Wegintegral berechnet man einen Komplizierten Weg aus oo einfachen Wegen und beim Volumenintegral die Masse aus oo Massenpunkten, oder?

Zuerst eine Frage zum Wegintegral. Was heißt, über den Weg C integrieren? Sind dann r1 und r2 einfach die obere und untere Grenze?

Und noch eine zum Volumenintegral. Die Formel für das Massenelement ist ja rho(ri)*V(ri). Wieso ist das in der Integration eine andere Formel? Wieso ist da die Formel rho* Funktion*V?

Allerdings, bei einer Integration von z.B. (2*x+4) dx wird ja das dx nicht mitgerechnet, sondern heißt nur, dass x die Variable ist. Heißt das dann, dass dV auch nicht mitgerechnet wird? Aber ich dachte, die Masse ist rho *V?

Und hier gibt es beim el. Feld auch sowas. Das ist auch ein Volumenintegral. Also wenn man statt der normalen Dichte die Ladungsdichte nimmt, kommt statt m Q raus, oder? Und für das el. Feld wird rho einfach nur mit der Punktladungsformel multipliziert, oder? Wieso genau? Und da steht d^3R. Heißt das, man soll die Integration dreimal mit den x, y, z-Kordinate von R machen, und dann multiplizieren?

A=(-3|0); B=(6|0); C=(12|8)

Ich würde mich sehr über Lösung und Rechenschritte freuen, danke.

Wie bekomme ich den Abstand der Geraden zum Ursprung?

Die Gerade: g: 3x+2y=13

Und welcher Punkt der Geraden g hat vom Ursprung den kürzesten Abstand?

Ich würde mich sehr über Lösung und Rechenschritte freuen, danke.

Wenn U(t) konstant ist, gibt es keine Änderung, also ist i(t) = 0. Wo ist mein Widerspruch?

Ich sitze gerade bei aufgabe 2.2 und ich bin Ehrlich gesagt sehr verwirrt. Ich bin nicht sonderlich gut im Mathe und habe daher große schwierigkeiten damit.

Kann jemand mir schritt für sagen was ich bei Aufgabe 2.2 machen soll? Mir ist zwar zum teil klar was die aufgabe will was ich berechne aber ich habe gerade irgendwie garnichts mehr im kopf.

Bitte schreibt aber detailiert was ich da machen muss.. danke

Bspw. Sind die Nullstellen

-2,57

0,89

2,39

Wenn ich eins dieser Zahlen nehme kommt keine Null am ende raus.

Wenn es zwei Inertialsysteme gibt und man etwas, das in dem einem System passiert, mit dem anderen System erklärt, ist das doch eine Galilei-Transformation, oder? Also mit Koordinatensystemen würde es von beiden Koordinatensystemen Ortsvektoren zu dem Punkt geben, wenn man die Sicht von beiden veranschaulichen will, oder?

Angenommen, 2 Kugeln mit unterschiedlicher Geschwindigkeit rollen aufeinander zu. Im Schwerpunktsystem bewegen sich die Kugeln mit gleichem Abstand auf den Ursprung zu, im Laborsystem sieht man aber, dass sich der Schwerpunkt bewegt. Also in dem Ortsvektor steht die Schwerpunktgeschwindigkeit, weil sich dadurch die Systeme unterscheiden, oder? Oder nicht? Also heißt das, wenn jedes mal, wenn ich eine Schwerpunktgeschwindigkeit rausfinde, habe ich so eine Transformation gemacht? Oder gehört in den Vektor noch mehr rein?

Aber irgendwie kann ich mir gar nichts unter der Zeichnung vorstellen. Okay, es geht um die 2 Bezugssysteme, man hat einen Vektor, der den Unterschied zeigt (?), und die anderen Beiden zeigen, wie irgendwas aus der Sicht von beiden Bezugssystemen aussieht. Aber was heißt das konkret? Was bedeutet der Punkt, auf den beide hinzeigen? Wie kann man sich die Zeichnung in Bezug auf eine echte Situation vorstellen, auch was die Vektoren in dem Bezug bedeuten? Hat jemand ein Beispiel?

Hey, ich bin hier fast am ausrasten.

ich versuche schon die ganze herauszufinden was ich hier verdammt noch falsch mache. Ich soll mit zwei Koordinatengleichungen den Winkel bestimmen, aber warum auch immer bekomme ich nicht die selben Ergebnisse wie es in der Lösung steht..

Meine Rechnung

Lösung

Ich habe auch im Internet nach Rechnern geschaut und die bekommen die selben Ergebnisse wie in der Lösung. Also die Lösung ist eigentlich richtig (hätte ja sein können das die Lösung falsch wäre)

Ich habe auch natürlich geschaut wie man sowas generell berechnet und ich habe genau das getan was da stand, aber trotzdem sind meine Ergebnisse falsch! Ich sollte eigentlich 8/33 raus bekommen aber ich bekomme die ganze Zeit 6/(Wurzel 66) * (Wurzel 16) raus. Aber ich bekomme nie den Zähler die 8 raus.

hab ich irgendwas vergessen oder verschrieben oder so? Oder kann mich das Universum einfach nicht leiden?!

Ich würde mich auf eure Antworten freuen

Für was funktioniert diese Galilei Transformation? Also ich dachte, für die Transformation vom Labor und Schwerpunktsystem und andersherum. z.B. zwei Wagen, die sich aufeinander zubewegen, im SS ist im Ursprung der Schwerpunkt und im Laborsystem nicht, also z.B. Wenn man von außen draufschaut.

Jetzt hat irgendjemand ein anderes Beispiel genannt, also ein fahrender Zug, und man transformiert vom System des stehenden Beobachters in das System des Zuges. Hat das Beispiel überhaupt mit Transformation von Laborsystem ins Schwerpunktsystem zu tun? Oder funktioniert die Galilei Transformation auf mehrere Arten? Ist das erste Bild auch eine Galilei-Transformation? Und von welchem zu welchem System wird im 2. Bild transformiert, weil da auch was von Galilei-Transformation steht? Inertialsystem zu Schwerpunktsystem? Geht das mit allen Systemen, also Laborsystem, Inertialsystem, Schwerpunktsystem, beschleunigtes System? Aber wie könnte man dann von Inertialsystem zu Laborsystem transformieren, ist das nicht so gut wie das gleiche?

2a + b + 2c = 2

4a + b + 2c = 4

0a + b + 3c = 5

Ich kann dieses Gleichungssystem beispielsweise in R lösen und die Lösungen mit mod 11 in Z11 überführen (dort sind die ganzen Zahlen 0,1,2,3,4,5,6.....,10 enthalten). Dort würde dann 1,1,5 rauskommen. Aber damit kriege ich halt nicht alle Lösungen. Ich würde mich sehr über eine Lösung freuen. Denke mal, dass man, dass als Vektor angeben kann (vielleicht mit 1,1,5 als Stützvektor)? LG

Okay, also z.B. wenn zwei Wagen aufeinander zurollen, ist im Schwerpunktsystem der Schwerpunkt im Ursprung und der kann sich auch bewegen, wenn die beiden Wagen nicht dieselbe Geschwindigkeit haben.

Beim Laborsystem hingegen schaut man einfach von außen drauf, oder? Ist das soweit richtig?

Meine Frage, was bedeutet das im Bild? Also was bedeutet die Zeichnung? Zeigt das zwei Stöße mit unterschiedlichen Endsituationen und man vergleicht de Endimpulse mit zwei zusätzlichen Vektoren? Aber was hat das mit Labor- und Schwerpunktsystem zu tun?

Und da steht, dass man das eine ins andere transformieren kann. Aber wie geht sowas? Und hat jemand ein Beispiel?

hii!
Ich habe zu der Aufgabe 6a) eine Frage: Wie bestimme ich genau die Dachneigung? Das ist meine Ansatz:

Dachhöhe/ Dachtiefe= 3m/16m = 0,1875

also betrüge die Neigung für das vordere Dach 18,75 Grad, oder?

Wie bestimme ich den Winkel, unter welchem die Dachflächen zusammenstoßen?

Ich dachte, dass man dafür erst einmal jeweils eine Koordinatenform bestimmt (also paramterform aufstellen und diese in Koordinatenform umformen) und dann mit der Formel (siehe 2. Bild)

Was denkt ihr von meinen Ansätzen?
Danke schön im Voraus!!

Gerade habe ich fast alles zu Kreisbewegungen verstanden und bin jetzt dabei, das letzte Rätsel diesbezüglich zu knacken, und zwar die Beschleunigung.

Was ich eigentlich immer dachte, war, dass die Beschleunigung die 2. Ableitung von r ist. Ich meine, der Vektor von v ist ja auch die Ableitung von r.

Dementsprechend dachte ich, dass der Vektor von der Zentripetalbeschleunigung die 2. Ableitung von r ist, weil das von dem Vektorinhalt so passt, aber anscheinend steht davor nicht 2. zeitliche Ableitung von phi, sondern was anderes, deshalb fällt das schon mal weg?

Ist es stattdessen richtig, dass der eine Vektor von a antiparallel zu r ist, und der andere (anti)parallel zu v? Dann würde das, was im Vektor steht, schonmal Sinn machen.

Und das Zeug davor? Wenn die Vektoren einfach nur die (anti)parallele Version von einem anderen Vektor sind, hat das auch nichts mit Ableitung zu tun, oder? Heißt das, das Zeug vor den Beschleunigungsvektoren hat z.B. nichts mit der Kettenregel einer Ableitung zu tun, im Gegendatz zu dem Zeug vor V?

Oder sind die Vektoren doch Ableitungen von irgendwas? Wenn ja, ich dachte, a ist immer 2. Ableitung von r, wieso sind das dann unterschiedliche Vektoren?

Oder geht es bei dem Zeug davor einfach nur darum, wie lang der Vektor ist?

Also bei dem 2. dann w^2r, weil das die Länge eines normalen Beschleunigungsvektors ist, oder?

Und bei dem 1. Teil die Winkelbeschleunigung. In dem Fall hat dann R nichts mit der Beschleunigungsformel zu tun, weil die Winkelbeschleunigung nur d^2phi/dt^2 ist?

Also besteht die Gesamtbeschleunigung aus 2 Teilen, dabei geben die Vektoren die Richtung an und der Teil davor jeweils die Länge?

Oder hat das doch was mit Ableitung von v oder r zu tun?

Entschuldigt die lange Frage, ich hoffe, man konnte sie verstehen.

Und aus Interesse, Wieso ist da nur ein Vektor a aufgezeichnet?