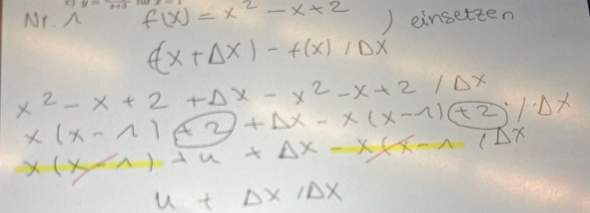Hey Liebe Community ich hoffe ihr könnt mir helfen.
Ich habe eine Aufgabe diese hier.
Lösen Sie dieses lineare Gleichungssystem mittels Gauss-Elimination
So hab es versucht bin gescheitert. Da habe ich mir die Lösung angesehen, jedoch verstehe ich da einen rechen schritt nicht. Besser gesagt kann ihn nicht nachvollziehen und zwar diesen hier.
Wie kann das sein das nun in der zweiten Zeile, die zweite und die dritte Zahl so aussehen? 1 - sprt(3) ist doch nicht -1 ? und das gleiche mit der dritten zahl das Ergebnis ist doch nicht 0? Hab ich was verpasst? Warum kommt das so raus in der Lösung. Logisch kommen die am ende mit einem schöneren Endergebnis raus als wie bei mir. Wenn so was erlaubt ist warum auch immer. Aber verstehe nicht warum oder wie die Regel da aussieht. So geht es weiter...
Warum wurde es so gelöst? Im Gaußsche eliminationsverfahren braucht es doch nur die Stufenform und das heißt hier es braucht nur das die Zahl unten links 0 werden muss oder nicht?
Kann mich vielleicht wer aufklären...