Wie bestimme ich alle Vektoren die orthogonal sind?
Folgende Aufgabe: Ich soll alle Vektoren bestimmen die zu Vektor - a und Vektor - b orthogonal sind.
Dabei ist der a - Vektor = (2/3/-1) und der b - Vektor = (5/-1/-2)
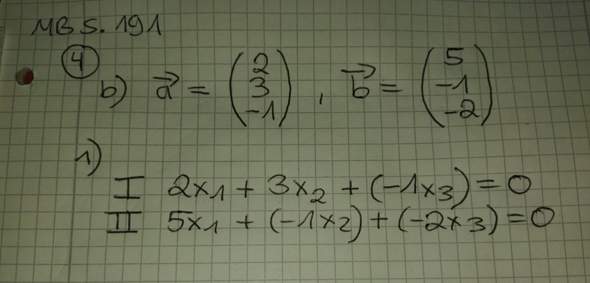
Ich konnte nachdem ich die Gleichung gleich Null gesetzt habe nicht weiter auflösen... vlt. wisst ihr da ja weiter
4 Antworten

Zwei Vektoren sind ja zueinander orthogonal, wenn ihr Skalarprodukt gleich null ist.
Ich würde einfach verschiedene möglichkeiten ausprobieren, also z.b. (2/3/-1)×(3/-2/0)=0
achso, soll der vektor zu beiden vektoren orthogonal sein?
Dann fällt mir spontan nur (0/0/0) ein;)

Hallo tomalo,
Da muss ich leider dazwischengrätschen, bevor noch falsche Zusammenhänge abgespeichert werden. Der Vektor (0/0/0) besitzt keine Länge und daher auch keine Richtung im Raum. Dementsprechend ist er auch nie parallel zu einem anderen Vektor.
Liebe Grüße

wir haben hier ein lineares Gleichungssystem (LGS) mit den Unbekannten,x1,x2 und x3 und nur 2 Gleichungen
Es gibt somit unendlich viele Lösungen
man kann 1 Unbekannte frei wählen.Wir wählen mal x3 frei wählbar
1) 2*x1+3*x2=1*x3
2) 5*x1-1*x2=2*x3
Beispiel:Wenn nun x3=1 dann ergeben sich daraus x1=.. und x2=...
hat die Form des LGS
1) a11*x+a12*y=b1 → b1=1*x3
2) a21*x+a22*y=b2 → b2=2*x3

Hallo,
auch ich möchte noch meinen Senf dazugeben. Die Idee von fjf100 war auf jeden Fall gut, allerdings geht es natürlich auch etwas simpler, wenngleich es abstrakter erscheinen mag.
Hast du denn schon vom Vektorprodukt - manchmal auch Kreuzprodukt genannt - gehört? Wenn ja kannst du es hier anwenden ;)
Damit ergibt sich Vektor_c = (7/1/17).
Da es uns nur auf die Richtung ankommt ist auch jedes Vielfaches von c eine Lösung für deine Aufgabe.
Liebe Grüße

Nachdem das Gleichungssystem mehr Zeichen als Variablen hat, hat es, glaub ich keine Lösung. Die Ausnahme ist, wie tomalo schon sagt, der Nullvektor.