Mathematik – die neusten Beiträge

Servus

dass man als elektriker Mathe braucht weiss ich ja, aber was genau machtvman denn in der verufssxhule für mathe, und wie schwer ist es? Gabe dieses jahr in mathe gerade so eine 3, letztes jahr hatte ich eine 4

lineare gleichungen ider wie auch immer kann ich bicht wirklich…

in physik hatten wir das mit den elektrik formeln nur kurz, die kann ich also nicht wirklich… lernt man das in der Berufsschule von null an?

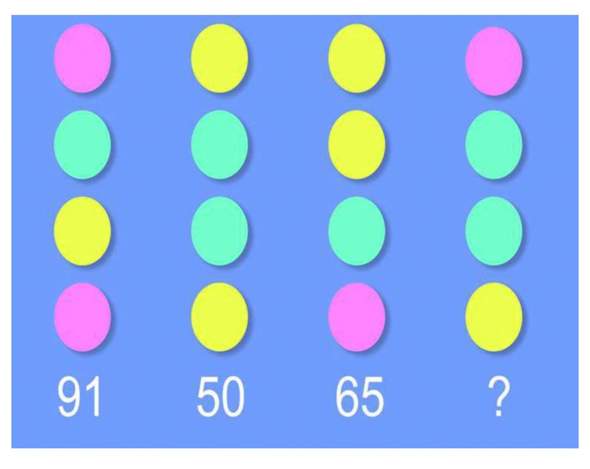
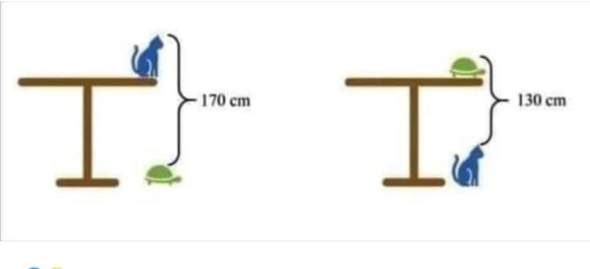
Da die Elektrolyse im tiefen Wasser relativ gleich effizient abläuft also gleich viel Watt je erzeugter Gasmenge benötigt wie an der Oberfläche habe ich mir gedacht. Warum nicht einen HHO Gasgenerator am unteren Ende einer Röhre aufstellen und ihn mit dem Gas eine Schaufelkette unter Wasser antreiben lassen. Ab einer bestimmten Wassertiefe müsste sich doch ein positiver Wert ergeben. Also eigentlich kein Perpetuum mobile aber ein Energiegenerator welcher die Energie aus dem Wasserdruck generiert gewisser maßen. Hier eine Skizze von dem Aufbau eines möglichen Experimentes.
Nun zu meiner Frage...

Wie berechne ich die mögliche Energiemenge die ein solches System theoretisch unter folgenden Vorraussetzungen produziert und sind meine Annahmen korrekt?

Widerstandskräfte werden außer acht gelassen.

Annahmen:

1kg = circa 10 Newton

1 W=F . s = 1 Joule = 1 Wattsekunde

1L Volumen des Gases entspricht 1kg Auftrieb

Wassertiefe bzw. Auftriebsweg 10m

Auf den 10 Metern sind insgesamt 10 Dosen mit je 1 Liter Fassungsvermögen.

Der Braungasgenerator produziert 6 Liter Gas je Minute.

Es sind also 10kg Auftrieb die Ihre Kraft auf das Zahnrad ausüben und sich mit 0,1m/s bewegen.

Da sich das Gas auf 10 Metern tiefe im doppelten Normaldruck befindet also 1 Bar wird es auf die halbe Größe komprimiert und hat somit auch die halbe Auftriebskraft. Der durchschnittliche Auftrieb einer Schaufel die mit 1 L Gas befüllt wird und sich von 10m Tiefe auf 0m Tiefe bewegt ist also ~ 0,75 kg, das Mittel von 0,5 kg ganz unten und 1 kg ganz oben.

1 N ist die Kraft die benötigt wird um ein Objekt mit 1kg um 1 Meter zu bewegen ganz herabgebrochen.

Mit einer mit Gas gefüllten Schaufelkette könnte ich 7,5 kg (75N) mit 0,1 Metern pro Sekunde innerhalb von 1Minute und 40 Sekunden über eine Strecke von 10 Metern bewegen.

Arbeit W=75.0,1/s²=7,5 Joule=7,5Ws

das entspricht 27000 Ws in der Stunde also 0,0075 KwH womit ich ein Gerät betreiben könnte was 7,5 Watt benötigt.

Damit wäre das Experiment sinnlos da erst bei einer Wassertiefe von sagen wir 4000 Metern ein sinnvoller Effekt eintreten würde.

W=20000.0,1/s²=2000Ws=7200000J/h=2kWh

Mit 2kW würde der 6LPM Gasgenerator vielleicht betrieben werden können wenn alles optimal läuft und so würden pro Stunde 360 Liter HHO Gas verwerten werden können. Das bringt dann theoretisch bis zu 60% von 2kWh also bekommst du bei der Anlage im besten Fall 1,2kWh heraus.

Keine Ahnung ob man das so rechnen kann aber das wäre mein erster Versuch. Wenn das nur ungefähr stimmt wäre das Experiment sinnlos!

Bitte kann sich wer die Mühe machen und das korrigieren oder verbessern weil ich bin kein Mathematiker oder Physiker und habe keine Ahnung ob ich auch nur im geringsten am richtigen Weg bin.

Quelle für die Annahme, dass HHO unter hohem Druck gleich effizient porduziert wird wie an der Oberfläche.

https://onlinelibrary.wiley.com/doi/abs/10.1002/bbpc.19340401009

https://www.fvee.de/fileadmin/publikationen/Themenhefte/th2004/th2004_03.pdf

Hey,

ich weiß das die Jacobi Matrix alle ersten Ableitungen beinhaltet. meine Frage bezieht sich auf die Funktion f(x,y) = cos(x²+y²). Davon möchte ich die Ableitung mithilfe des Differentialquotienten bilden. Ich kenne die ersten Ableitungen bereits jedoch benötige ich den Differentialquotient um nachzuweisen, dass überhaupt die ersten Ableitungen existieren. Nur steh ich ein wenig auf dem Schlauch was das einsetzten in den Differentialquotienten mit der h-Methode angeht. Ich weiß dass ich dafür das Additionstheorem benötige.

Sagen wir ihr müsst sieben Themen beherrschen. Und wie lange würdet ihr täglich lernen?

Geht um eine Bekannte, die letztes Jahr in ihre erste eigene Wohnung gezogen ist. Sie hat neulich die Jahresabrechnung bekommen, und muss über 1000 € für Kaltwasser nachzahlen.

Warmwasser wird extra abgerechnet. Dazu hat jeder einen Zähler in der Wohnung. Für Kaltwasser gibt es aber nur einen Zähler im Keller. Das Kaltwasser wird unter allen Bewohnern aufgeteilt. Das heißt, wenn jemand überdurchschnittlich viel verbraucht, müssen die anderen mit dafür zahlen.

Im Haus sind 6 Wohnungen. In jeder Wohnung lebt nur eine Person. Alle beziehen nur Hartz4 und können sich die Nachzahlung nicht leisten... Insgesamt wurden 2000 Kubikmeter Wasser zu viel verbraucht.

Jeder Bewohner muss also für 330 Kubikmeter Wasser nachzahlen. Ein Wasserrohrbruch wurde schon ausgeschlossen. Also woher kommt es, und was würdet ihr dagegen tun?

Hallo,

Könnte mir jemand ein Beispiel für dort unten für diese formale Darstellung geben? Ich verstehe die Zeichen, aber kann mir daraus kein alltägliches Beispiel rekonstruieren oder irgend ein banales Beispiel.
Ist dieses a jetzt eine Eigenschaft oder habe ich da was falsch verstanden?

Wir haben heute in der letzten Stunde eine Mathe-Arbeit. In einer Zeit wo man sich kaum noch konzentrieren kann!!!

Kann ich diesen Lehrer verklagen?

Was kann ich mir unter der Menge Ia:I vorstellen? Was bedeutet das a in diesem Zusammenhang und was bedeutet der Doppelpunkt?

Ich konnte die Frage selbst beantworten. Es handelt sich nicht um eine Menge. Ia ist einfach der Name der Funktion. Tut mir Leid, es ist noch früh.

Auf einem Laufband würde eine volle Flasche wasser,wenn man sie wagerecht hinlegen würde, langsamer ans Ende kommen als wenn man sie senkrecht hinlegen würde.

Mit was für einer Formel müsste ich rechnen damit die Flasche nie ans ende kommt?(also quasi da bleibt wo man sie hin gelegt hat)

Vielen Dank an alle Antworter die meine Frage beantworten :-)

ich bin 10. klasse und weiß einfach nicht was eine primzahl ist.

primzahlen kann man durch eins und sich selbst teilen, sie sind größer als 1 und sind ganze zahlen. Das weiß ich, aber irgendwie habe ich richtigen denkfehler.

2 durch 1 ist 2, 2 durch sich selbst ist doch 1.

3 durch 1 ist 3, 3 durhc sich selbst also 3 ist doch 1

4 durch 1 ist 4, 4 durch sich selbst (4 ist doch 1)

bin 10. und fühl mich richtig dämlich.

häää

Ich schaue gerade ein Youtube Video in dem eine Mathe Frage vorkam, die hiess: Write down the decimal fraction equivalent to 9/2000. Was bedeutet das im Deutschen? Die Lösung ist 9.002

Eine klassische Aufgabe:

Zwei Autos machen ein Autorennen:

Auto A fährt durchschnittlich 115km/h

Auto B fährt eine halbe Stunde später los mit 100km/h

Wieviel Strecke haben die beiden jeweils zurückgelegt, wenn sie sich treffen?

Bei konstanter Geschwindigkeit, wäre das jetzt kein Problem, aber ich weiß nicht genau wie ich das machen soll mit einer durchschnittlicher Geschwindigkeit. Kann mir jemand helfen?

Hallo, es gibt 2 Aufgaben die wirklich mir den Kopf zerbrechen da ich wahrscheinlich zu dumm bin um das zu rechnen xD

Aufgabe: Setze die Fehlenden Klammern ein

66-22:11×4+8=768

66-22:11×4+8=9

Hääää irgendwie bekomem ich das Ergebnis nicht so hin 😂

Wieso können nicht alle 200 cm hoch sein? Ich Stoß mir mit meinen 186 cm ständig den Kopf,wenn ich mich nicht bücke.

Wie lange dauert der Download, wenn 8.5 GB heruntergeladen werden und die Geschwindigkeit 3.5 MB/Sek. beträgt?

Das tiefste was ich bisher gesehen habe,war 4,05 m tief.

Hallo, ich übe grade für eine Mathe Klausur und soll sagen ob das stimmt und es dann begründen:

Die Menge {p0, p1, p2, p3} bildet eine Basis des Vektorraums II3 der Polynome vom Höchstgrad 3, wobei p0(x) = 3, p1(x) = 3 + 2x, p2 (x) = 3-4x+x^2, p3 (x) = x^3.

Ich weiß, dass eine Menge eine Basis bildet, wenn die Vektoren linear unabhängig voneinander sind, jedoch weiß ich nicht wie ich hier vorgehen muss, weil es keine Vektoren sind.

Hallo. Bin in 4. Semester meines Mathe Studiums und will als data science arbeiten. Wie muss ich dementsprechend mein Studium fortsetzten? Welche Fächer soll ich wählen? Und soll ich mein Master machen, wenn ja in was, oder reicht ein Bachelor? Wie müssen die Noten sein und in was sollte ich am besten meine Bachelor Arbeit schreiben? Danke

Hey, beschreibt die Taylorentwicklung 1. Ordnung auch die 1. Ableitung einer Funktion, sprich die Steigung? Und damit wenn die Taylorentwicklung 1 Ordnung die Steigung 0 hat, dann haben wir Extrema?

Hab da einen Verständnishänger. Beim Würfeln gibt es ja 6 Möglichkeiten, eine Zahl zu werfen, also ist für jede Zahl die Wahrscheinlichkeit 1/6. Bei der Wahrscheinlichkeit von Regen gibt es doch zu einem bestimmten Zeitpunkt nur zwei Möglichkeiten: Entweder es regnet oder nicht. Also ist doch nur eine Regenwahrscheinlichkeit von 50% innerhalb eines bestimmten Zeitfensters möglich. Was kapier ich da nicht?

Ich spiele mit den Gedanken, ob ich Informatik studieren soll, oder doch eine Ausbildung als Polizist mache, deswegen informiere ich mich erstmal so gut ich kann über die Polizei.

Muss man als Polizist oft Kopfrechnen bzw gute Mathe Kenntnisse haben?

Wenn ich 4 Mittelwerte habe kann man aus diesen 4 Mittelwerten einen Gesamtmittelwert berechnen, nein oder? Zumindest dann nicht wenn die Anzahl der Werte zwischen Mittelwert 1,2,3 &4 unterschiedlich ist, richtig?

welche farbe hat euer mathe heft / ordner / was auch immer?

Hallo!

Ich sollte eig. in den Ferien Mathe und Englisch lernen was ich auch mache aber ich schiebe es immer ein paar Tage vor mich hin und mir fehlt einfach die Motivation und meine eigentliche Frage jetzt:

Was kann ich machen, damit ich mehr Motivation habe?

Lg,

Hallo zusammen,

ich bin gerade dabei unser automatisiertes Lager optimieren und möchte gerne mal eure Meinung hören.
Es hört sich eigentlich recht einfach an ist aber durchaus ein bisschen schwerer als man denkt.

Gegebenheiten & Problemstellung:

Und zwar haben wir verscchiedene Pack/Pickplätze, die unterschiedlich schnell arbeiten (Die Durchschnittlichen Zeiten pro Platz sind bekannt) und von dem gleichen Förderband bedient werden. Die Frage ist nun wie schnell man neue Wahren auf das Förderband stellen muss damit jeder Picker arbeiten kann und keine Däumchen drehen muss. Gleichzeitig soll das Fliesband allerdings nicht zu viel bekommen, sodass die Picker überfordert werden.

Beispiel:

Pickplatz 1 : 2 min Packzeit
Pickplatz 2 : 1 min Pickzeit
Pickplatz 3 : 4 min Pickzeit
Pickplatz 4 : 2 min Pickzeit
...

Die Wegzeit sowie die maximalmögliche Zeit die unser Lager schafft um neue Waren auf das Förderband zustellen kann hieberi vorerst vernachlässigt werden und ist für diese Frage nicht relevant.

Ein Kollege von mir wollte jetzt den Durchschnitt erechnen und in diesem Tempo Waren nachliefern. Da habe ich jetzt aber widersprochen, da ich der Meinung bin, dass jeder der jetzt unter dem Durchschnitt liegt zu langsam bedient werden würde.

Meine erste Idee war deshalb die Zeit des schnellsten zu nehmen. Das wiederum könnte zu viel sein...

Nachdem ich nun 15min drüber nachgedacht habe, bin ich zu folgendem Schluss gekommen: Ich glaube wichtig sind nur die Extreme bzw. die längste Zeit die ein Pickplatz braucht.

Folgenden Algorithmus habe ich mir jetzt ausgedacht:

Für jeden Pickplatz erechne ich mir wie viel Nachschub er innerhalb von der Zeitspanne des langsamsten Pickplatzes benötigt. Hier anhand des Beispiels:

Pickplatz 1: 4/2 = 2 x Nachschub innerhalb von 4 Minuten
Pickplatz 2: 4/1 = 4 x Nachschub innerhalb von 4 Minuten
Pickplatz 3: 4/4 = 1 x Nachschub innerhalb von 4 Minuten
Pickplatz 4: 4/2 = 2 x Nachschub innerhalb von 4 Minuten

Davon bilde ich jetzt die Summe, sprich innerhalb von 4 Minuten benötige ich 9 x Nachschub.

Daraus ergibt sich: 4/9 = Alle 0,44 Minuten muss ich Nachschub auf das Band bringen damit jeder dauerhaft was zu tun hat.

Meine Frage:

Was sagt ihr? Ist das dann wirklich die optimale Nachschubzeit oder würdet ihr das anders machen?

Ich bin mir sicher, dass viele andere schon dieses Problem hatten. Leider finde ich aber nicht die richtigen Begriffe um erfolgreich zu googeln und wirklich eine Kalkulation zu finden.

Ich verstehe den schritt nicht wie man auf die Präambel und Nutzdaten kommt. Was genau ist überhaupt eine Präambel?

Hallo. Studiere zurzeit Mathe und hab nächstes Jahr meinen Bachelor. Habe überlegt meinen Master in Wirtschaftsmathematik (an einer anderen Uni) statt Mathematik zu machen, da ich ebenfalls für Wirtschaft und Finanzen mich interessiert. Wie sehen sie Berufschancen als wirtschaftsmathematiker aus? Oder lieber doch in Mathe meinen Master machen? Oder sollte ich lieber im Bachelor Studium beides Dual machen und dann direkt arbeiten? Danke

Komme bei der Aufgabe im Titel nicht weiter. Ich habe gegoogelt wie man das ausrechnet aber durch meine Rechenschwäche verstehe ich gar nichts. Vielleicht kann mir hier jemand helfen...

Ich habe vor kurzem mein Abitur geschrieben und 15 Punkte in Mathematik erreicht.

Das Fach hat mir nie Probleme bereitet und gehörte immer zu meinem Lieblingsfächern,doch das scheint eher eine Ausnahme zu sein.

An die "Mathehasser":

Warum hasst ihr die Mathematik?

Habt ihr irgendwann in Mathematik aufgegeben?

Hier die 1. Aufgabe:

(a) Finden Sie a,b,c>0, so dass gilt:

(17x+4z)² − 9 = (ax+4z+3)(−3+bx+cz)

a= ?

b= ?

c= ?

Ich hatte a=17, b=17, c=8 was beim Ausrechnen falsch war

Hier die 2. Aufgabe:

(b) Finden Sie ganze Zahlen a,b,c,d, so dass für alle reellen Zahlen x,y,z gilt:

(10x+5z)²−(3x−10y)² = (ax+5z+by)(−10y+cx+dz)

a= ?

b= ?

c= ?

d= ?

Ich hatte a=1, b=-6, c=1, d=5 was beim Ausrechnen auch falsch war

Könntet Ihr bei Antworten den Rechenweg mitgeben, damit ich verstehen kann wie man so eine Aufgabe lösen kann?
Vielen Dank schonmal im Voraus für die Antworten 😊

hallo,

schon in Teenagerzeiten bemerkte ich es.

Meine Freundin sagte mal, dass der weg 1km wäre.

Als ich fragte wie viel/wie weit denn 1 km ist, bis wohin ungefähr ein Weg 1km wäre, meinte sie weist du das nicht

Ich kann mir das echt nicht vorstellen.

Nie.

Auch wenn meine Eltern über 15km sprechen. Mir sagt das nicht. 1 km sind 1000schritte aber so ungefähr weiß ich vllt von wo bis wo 1km wären aber 10könnte ich mir nicht vorstellen oder mehr.

Ist das normal? Oder bin ich echt dumm.

Ich glaube das ist normal, kann passieren, wenn man nicht so oft am Auto fahren ist oder Mathe einen nie interessiert hat.

Ein Freund meinte auch mal zu mir, dass seine Schwester nicht weiß wie viel zb.200kmh wären beim Autofahren. also wie schnell dann das Auto fährt.

Das weiß ich auch nicht

Könnt ihr mir den Rechenweg erklären?

Es heißt doch "Die Klammer sagt, 'Zuerst komm ich'" also 8÷2(4) und dann geht es weiter mit "Danach rechne Punkt vor Strich" also 4(4) und vor der Klammer steht doch dann immer ein Mal-Zeichen also 4×4=16, wieso sagen die Anderen 14?

Kann es ein Polynom geben, deren Ableitung und es selbst keine Nullstellen haben?

Von den Besuchern eines 2-tägigen Musikfestivals sind 30% nur am 1. Tag sowie 20% nur am 2. Tag auf dem Festivalgelände anwesend (die restlichen 50% sind an beiden Tagen auf dem Festivalgelände anwesend).

1. Wie wahrscheinlich ist es, dass ein (zufällig ausgewählter) Besucher, der am 1.Tag auf dem Festivalgelände anwesend war, auch am 2. Tag auf dem Festivalgelände anwesend ist?
2. Wie wahrscheinlich ist es, dass ein (zufällig ausgewählter) Besucher, der am 2.Tag auf dem Festivalgelände anwesend ist, nicht schon am 1. Tag auf dem Festivalgelände anwesend war?

Liebe Grüße

Unter jeder Kugel-Kolonne steht ein Zahlenwert. 

Was für ein Wert steht unter der letzten Kolonne?

Hallo,

Ich bin nicht gut in Mathe nicht weil ich nicht lerne ganz im Gegenteil ich lerne viel. Hat jemand Tipps wie man in Mathe besser wird? Auch wenn ich lerne schaffe ich trotzdem nur schwache Noten.

Hallo.

wenn 300ml Wasser + 3 Löffel Pulver = 400kcal ergeben, wie viel ergeben dann 400ml Wasser + 4 Löffel Pulver? (Shakezubereitung)

Aufgabe auf dem Bild. Es geht um 2a).

Hey ihr lieben :)

Kennt ihr Rätsel/ Logikfragen, die so ähnlich sind wie das Josephus-Problem?

Anders gefragt: Ich suche coole Logikrätsel.

Danke!

Hii

Ich würde gerne Mathe LK wählen und wollte fragen, welche Themen drankommen.

 Ein PKW fährt mit einer Geschwindigkeit von 80 km/h. Der Fahrer bemerkt in 65m Entfernung ein Hindernis und bremst nach einer Reaktionszeit von 0,8 sec mit einer negativen Beschleunigung von – 6,0 m/s² ab. 

Kommt das Fahrzeug rechtzeitig zum Stillstand?

Stimmt das so?

80 km/h /3,6 = 22,22 m/s

22,22m/s *0,8 s = 17,8 m = Reaktionsweg

v/a=t = 22,22m/s * -6m/s² = 3,7s

s= 1/2*(-6) * 3.7²

s= -41,15 m = Bremsweg

Falls das Ergebnis des Bremsweg stimmt, macht das wirklich Sinn, dass da ein Minus als Vorzeichen steht.

Ein Pentagon-Dodekaeder, dessen Flächen mit den Zahlen von 1-12 belegt sind, wird 1500 Mal geworfen. Die Zufallsgröße X sei die Anzahl der dabei erhaltenen Einsen.

Bestimme die Zahl der zu erwartenden „Einsen“, die Varianz und die Standardabweichung?

Hii,

also ich hab hier diese Frage und finde keinen Rechenweg bzw. bin mir nicht sicher ob ich das so rechnen kann wie ich es mir denke. Also wäre schön wenn mir jemand helfen kann. Danke im Vorraus.

Ich weiß "einfach" ist relativ. Aber welche Studiengänge würdet ihr als einfach beschreiben. Mathe-lastig sollte er auch nicht sein. Jobchancen und Verdienst wären auch wichtig. Danke.

Hallo,

Ich wollte meine Arbeit ein wenig erleichtern und könnte die Arbeit mit einem Parkhaus Gebühren rechner das ganze verschnellern. Es kann ne App, website oder ein Programm sein ganz egal.

Ich bräuchte eine Gebühren feld die ich angeben kann und am besten die Einfahrt Zeit die dann das Automatisch berechnet mit der Aktuellen Zeit bzw. System Zeit.

Das heißt beispielsweise:

Parkhaus 1 Je Stunde = 2 Euro

Einfahrt Uhrzeit : war Beispiel 12:00

Wir haben jetzt Aktuell 12:58 das heißt der Kunde muss 2 Euro bezahlen.

So einen Rechner benötige ich da ich über 120 Parkhäuser betreue und solche Rechnungen manchmal 6-7 mal gleichzeitig machen muss. Da würde ein Rechner echt helfen. Der Tadchenrechner ist mir zu langsam.

Vielen Dank für die Hilfe schon mal

(Das Monty hall Problem ist das mit den 3 Türen, hinter denen 2 Ziegen und 1 Gewinn ist/sind) Ich habe mit diverse Erklärungen angeschaut aber ich verstehe es einfach nicht. Vereinfacht ist das wie ein Sack Kugeln mit 2 roten und einer blauen und es ist im Prinzip einfach Kugeln herausnehmen ohne sie zurück zu legen. Da müsste sich doch die Chance immer weiter angleichen an die blaue Kugel (sprich von 1/3 zu 1/2)

ich würde schätzen 1.88 ca oder?

Ein anderer Nutzer hatte eben in seiner Frage stehen: "Ich weiß das man leichter wird wenn man dort hin reist."

Stimmt das?

Wie viel weniger wird es sein?

Nehmen wir an, eine Person ist 180cm groß und reist von Deutschland zum Äquator, ist sie dann dort größer, z.B. 183cm?

Ich weiß das man leichter wird wenn man dort hin reist. Da die Erde ein Ellipsoid ist aufgrund der Fliehkraft, ist sie am Äquator mehr ausgebeult und man ist vom Erdmittelpunkt daher weiter entfernt als in Deutschland.

Deshalb hat die ESA den europäischen Weltraumbahnhof auch im französischen Überseegebiet Französisch-Guyana errichtet, weil der Raketenstart wegen der Äquatornähe dort weniger Energie benötigt als in Kontinentaleuropa.

Die Gravitation müsste also den Körper in Deutschland mehr anziehen als am Äquator und die Wirbelsäule mehr zusammendrücken als dort. Wie viel cm kann das ausmachen und kann man das berechnen?

Das Ergebnis ist angeblich 8,31084E-07. Was soll das -07 am Ende? Und so eine große Zahl ergibt keinen Sinn. Ich habe keine Ahnung wie ich das interpretieren soll.

Bild im Anhang.

Würde mich extem über (schnelle) Hilfe freuen!

Wie im Titel schon steht hab ich halt ein Problem mit Mathe (schlechtes Zeugnis) und muss mich in Mathe verbessern. Allerdings mangelt es mir vor allem an den Grundlagen und da frag ich mich, wie ich das alles aufholen und repetieren soll. Manche Themen erscheinen einfach aber mit neuen Themen kombiniert mache ich dann trotzdem Fehler. War jemand schon mal in dieser Lage und wie habt ihr euch verbessert? Hat jemand eine Empfehlung für ein gutes Buch oder sonst etwas hilfreiches?

P.S: bin in der 11. Klasse

Ist Alan Turing wirklich die Galionsfigur der LGBTQ-Bewegung?

Das hat ein Kommiliton gesagt,als er die Turing-Maschine ansprach.

Hallo,

in der Definiton eines Vektorraums kommt die Verknüpfung mit mal und plus vor. Aber wieso? Haben diese Rechenarten so eine große Bedeutung? Liegt es daran, dass ein Vektorraum ein Körper ist?

Ist ein Vektorraum dann einfach eine Menge von Vektoren, egal ob Ortsvektor oder nicht, die dann in diesem Raum bzw. Ebene liegen?

Danke

Hi, ich vermute, dass man die Jordan-Normalform allein durch die Informationen bestimmen kann, die man gegeben hat:

Ich schließe daraus, dass die alg. V. von lambda1 & 2 jeweils 1 ist (und geometrische vielfachheit ist für lambda1 und/oder lambda 2 ungleich 1)

Gibt es dann nicht eh nur eine Möglichkeit die Jordan-Normalform darzustellen?

Wäre es in diesem Fall nicht egal, wie hoch geometrische Vielfachheit ist? Denn so oder so, haben wir doch nur zwei verschiedene Eigenwerte, die nicht mehr oder weniger Jordan-Block-Anordnungen haben können, als eine einzige, oder? Diesen speziellen Fall habe ich noch nie behandelt, daher weiß ich nicht, ob ich da komplett falsch liege.

Eine komplett neue Klasse, eine komplett neue Schule von der ich nichts gehört hatte.Da es mein erstes mal nach 5 Jahren ist, wollte ich fragen wie ihr denn zurecht gekommen seid, als ihr einen Schulwechsel hattet. (In meinem Fall 11.Klasse)

Was muss ich beachten?

Hallo ich bin Student und da ich bald eine Mathe Klausur schreibe wollte ich mit den Aufgaben die bei uns im Kurs sind mich vorbereiten. Ich studiere einen Ingenieursstudiengang. Die Lösungen befinden sind ebenfalls auf der Plattform. Jedoch sobald ich versuche eine Aufgabe alleine zu lösen bekomme ich nichts geschissen. Immer muss ich in die Lösungen kurz reinschauen und dann versuche ich es nochmal selber. Bis ich die Aufgabe auswendig kann ohne Lösungshilfe. Das mustert wiederholt sich aber bei jeder Aufgabe. Bis jetzt hatte ich bei 30 von 30 Aufgaben alle samt erstmal kurz Lösung abgecheckt bevor mir was einfiel und ich vorankam. Aber ich finde das ist nicht normal. OK man könnte jetzt sagen Mathe ist ein Anwendungsfach indem das lernen auf die Wiederholung ankommt. Aber in ner Klausur muss man ja irgendwie die Aufgaben selbstständig lösen können. Das ist bei mir aber nicht gegeben. Ich bekomme selbständig einfach nix gebacken und komme mir deshalb verdammt dumm wie Brot vor

Was soll ich machen? Ich verzweifle

Hallo,

ich hab ehrlich gesagt nichtmal einen Plan wie man so ein Gebiet nennen soll, ist ja wie „Land“ kaufen, nur eben als Fläche auf dem Wasser. Z. B. 1000ha Ozean mitten im Atlantik.

Kann man soetwas reintheoretisch kaufen? Das ist ja dann eigentlich internationales Gebiet, vor Küsten ggf. noch zu einem Staat zugehörig, kann man das irgendwie in Privatbesitz bringen? Mir ist die Frage gerade in den Kopf gekommen und ich habe echt nichts dazu im Internet gefunden :)

LG,

Theo

Hallo 🖐🏻, 

kann mir jemand mal den Studiengang Mathe + Wirtschaftswissenschaften Lehramt davon erzählen? Also eure Erfahrungen, das würde mich echt interessieren und vor allem die Kombination aus den beiden Fächern.

Danke schon mal im Voraus

Wann muss ich beginnen zu lernen, wenn ich bis einschließlich 1. September Zeit habe und auf den Tag genau 4 Wochen lang lernen möchte?

Kann man Fakultät von dezimalzahlen berechnen, also zum Beispiel !7,35184

Und wenn ja, wie?

Nr 6

Wie heißt dieser Aufgabentyp (nicht "Gut kombiniert" :D)

Hallo, kann mir einer, der/die eine kaufmännische Ausbildung macht/ gemacht hat sagen, welche Themen in Mathe vorkommen? Also welche Themen erarbeitet man im Unterricht?

Hallo,

Ich habe dazu ein Beispiel gemacht. Stimmt er ?

Wenn er stimmt, wie kann dann 1 äquivalent zu 2 sein und umgekehrt? Das sind doch nie im Leben Äquivalente Elemente zueinander.

Also bspw. 13245, 14532,... usw...

oder wie kann man ausrechnen, wie viele Möglichkeiten es gibt?

Hallo ich bräuchte bei folgender Aufgabenstellung Hilfe:

a) und b) habe ich bereits fertig:

Bei c) weiß ich dann allerdings nicht mehr ganz weiter:

Wie komme ich jetzt vom Phasenhub auf die Regelparameter?

Hey,

angenommen ich kaufe im Online Shop Artikel im Wert von 100€, kriege dann aber 20% Rabatt und bezahle somit 80€ für alles. Wenn ich dann einen Artikel der genau 20€ gekostet hat behalte, heißt dass dann, dass der geschenkt war, weil ich ja 20€ Rabatt bekommen habe?

hello

fragt der BMT 10 das Wissen der 10ten Klasse ab?

ist oben

Wer kennt die Lösung?

Hi

Ich stehe vor der Wahl zwischen Informatik (in Kassel) und angewandter Informatik (in Göttingen) als Studiumswahl. Ich tendiere eher zu angewandter Informatik, da der Mathe-Anteil geringer ist, jedoch scheint die Uni in Göttingen - laut Erzählungen - härter zu sein. Was würdet ihr tun? Das leichtere Studium an der vermeintlich härteren Uni oder das härtere Studium an der leichteren Uni?

Zu mir: Ich habe von beiden Studiengängen kaum Ahnung bis auf die Infos aus YouTube-Videos, bin jedoch offen dafür und lernbereit (dennoch nicht sonderlich gut in Mathe).

Die Mathematik ist meine große Liebe und ich kann mir keine schönere Beschäftigung vorstellen.

Diese Schönheit der Logik bezaubert mich immer wieder.

Nichts kann damit verglichen werden.

Ich frage mich immer,warum Personen andere Personen lieben,das ist für mich nicht nachvollziehbar.

Versteht ihr das?

Eine Seilwinde hat eine Nennleistung von 15000 Nm/s. Zum Anheben einer Last von 700kg über eine Höhendifferenz von 23m werden 15s benötigt.

1. Wieviel Prozent der Nennleistung beträgt die Nutzleistung?

2. Welche Wärmemenge entsteht aus der verlorenen mechanischen Energie infolge der Reibung?

Aufgabe 1 ergibt 10529,4 Nm/s, also 68,63 %.

Wie soll ich jetzt 2 berechnen, ich habe da gar keinen Ansatz.

Soll ich 10529,4/700*9,81 oder 700*9,81*10529,4 rechnen?

Erstmal die Frage: Macht das überhaupt Sinn?

Naja

7pi/2 mod 2pi = (2pi + 3/2pi) mod 2pi = 3/2pi das zu behaupten scheint ja erstmal logisch, zumindest für mich.

pi mod e = pi - e approx. 0,42

PS: Ich hab keine Ahnung von irgendwelchen Rechengesetzen die in Zusammenhang mit Modulo existieren. Deswegen frage ich.

Wenn x^3 positiv ist dann ist x imaginär oder?

Ich brauche eine gute Erklärung mit Beweisführung!

(Ist für einen Freund!)

zb wenn nichts in der Aufgabe von runden steht ,soll ich dann trotzdem runden oder nicht ,und auf welcher Zahl soll ich runden 10 ,100, 1000er ??

Ich hab ein Problem ich Weiß oft nicht wann ich runden soll und wie (wenn nichts in der Aufgabe steht)

aufgabe b)

Bitte nicht so kompliziert auf schreiben👍
aufgabe 5

Wir haben ein Sonnensystem bestehend aus einer Sonne und drei Planeten.

Die Sonne ist der Mittelpunkt des Systems und die Planeten kreisen in unterschiedlichen Abständen um eben diese.

Planet 1:

Der äußerste Planet befindet sich exakt nördlich der Sonne und benötigt 30 Jahre um diese zu umkreisen.

Planet 2:

Der mittlere Planet befindet sich exakt nördlich der Sonne und benötigt 2 Jahre um diese zu umkreisen.

Planet 3: 

Der innere Planet befindet sich exakt östlich der Sonne und benötigt 1 Jahr um diese zu umkreisen.

Ich blick nicht durch XD.

Ich habe eine alte Küchenwaage in den Tiefen meines Schrankes gefunden und wollte damit mein Essen abwiegen und bin davon ausgegangen, dass die Zahlen für die jeweiligen Gramm stehen. Also 200 = 200 g und da die Waage in Zweihunderter-Schritten funktioniert, wäre der etwas längere Strich zwischen der 0 und der 200 die 100g.

Jedoch habe ich als Test erst einmal 100 g Speck(es müssen 100 g sein, da dies auf der Verpackung steht) auf die Waage gelegt und die 100 g werden mir so angezeigt:

Warum ist das so merkwürdig konstruiert?

Hallo

Das heißt, dieses Tilde ~ Zeichen steht für eine Äquivalenzrelation, und auch für eine Äquivalenzzeichen, wie z.B. das Gleichheitszeichen = , oder kongruent ≡, und so weiter...

Oder?

Hallo,

1267(hex) ist in vorzeichenloser Betrachtung in Dezimal 4711.

Und wenn man es nun im Zweierkomplement betrachtet, dann doch auch, oder?

Das höchstwertigste Bit ist ja nicht 1, demnach auch Dezimal 4711, oder?

LG

Sehr geehrte Damen und Herren.

Ich hoffe sehr, dass Sie mein Problem verstehen und versuche es klar und deutlich zu schildern. Bei Rückfragen zu meinem Problem stehe ich Ihnen gerne zur Verfügung.

Ich habe mich vor Kurzem für einen zulassungsbeschränkten Studiengang beworben, da die Bewerbungsfrist der 31.07.2021 ist. Nun hab ich für die nächste Woche einen Urlaub von zwei Wochen geplant und möchte daher wissen, wann man die Zulassungsbescheide bekommt( falls man denn zugelassen wird) und wie lange Zeit man dann endgültig zur Immatrikulation hat. Leider habe ich auf der Webseite der Universität keine genaueren Infos dazu herausfinden können, nur dass die Frist dann auf dem Zulassungsbescheid stehen würde, aber nicht wann man denn genau bekommt. Muss bis zur Immatrikulationsfrist dann auch der Semesterbeitrag eingegangen sein? Meine Befürchtung wäre eben, dass dieser Fristtermin mitten in meinem Urlaub liegt und ich dementsprechend mich nicht mehr einschreiben kann. Oder ist die Immatrikulationsfrist mindestens bis September?

Es tut mir leid, dass ich so viel Text geschrieben habe, aber diese Frage wäre für mich wichtig, da ich wissen muss, bis wann man sich immatrikulieren muss und wann man im Fall der Zulassung die Zulassungsbescheide erhält( die Frist für Bewerbungen generell ist ja der 31.7). Bei Bedarf kann ich Ihnen gerne den Namen der Universität nennen.

Mit freundlichen Grüßen

burger3354

So Eben hab ich einen riesen Sack (ca. 30l) ins neu angekommene Gehege gekippt. Nun siehts so aus. Stall: 60cm hoch, 60cm breit, 120cm lang muss um die 40-50% gefüllt werden. 1 Sack hat hier nicht gereicht. Ich konnte nur 1/4 bis 1/3 der geünschen Menge an Höhe befüllen. Da ich noch nie so viel Streu brauchte kenn ich mich nicht aus.

Nun ist eure Meinung gefragt: In der Zoohandlung gibt es Kleine, Mittlere und Große Säcke (also 10, 30, 60 liter). Eure grobe Schätzung wie viel an Streu muss ich noch ca. einfüllen damit ich weiß wie viel ich noch ungefähr kaufen muss (plus ne kleine Reserve)

Aufgabe 4

Heyo, ich (M,13) habe heute mein Zeugnis bekommen, und bin irgendwie traurig, dass ich nicht nur 1 habe. Mein Zeugnisdurchschnitt ist 1,4 und es gefällt mir einfach nicht. Ich gehe auf ein Gymnasium, und jeder aus meiner Klasse übertreibt, dass ich übertreibe… aber ich bin ehrlich unzufrieden mit den Noten:

Mathe: 1

Deutsch: 2

Englisch: 2

Französisch: 2

Biologie: 2

Sport: 1

Musik: 1

Kunst: 1

Religion: 1

Geschichte: 1

Meine Fragen lauten:

Stimmt es dass ich übertreibe?

Wieso will ich in allen Fächern eine 1?

Auch wenn ich der Klassenbeste bin an einem Gymnasium was ein Erfolg ist, bin ich damit unzufrieden, wieso?

Dankiii 💞🥰 für jede einzelne Antwort…

a) Die Oma von Lisa ist fünfmal so alt wie sie. In 4 Jahren ist die Oma nur noch vier mal so alt wie Lisa. Wie alt sind Lisa und ihre Oma?

b) Max und Paul haben zusammen 100 murmeln. Nachdem Max 25 Murmeln von Paul gewonnen hat, hat Max dreimal soviel wie Paul. Wie viele murmeln hatten Paul und Max am Anfang?

Viel lernen bringt bei mir nichts, ich verstehe vieles sehr leicht aber in mathe verstehe ich die themen so schwer und mein kopf zerbricht immer. Ich bekomme mit 3 wochen lernen vor der Probe Eine 3 die auch noch fast eine 4 wäre.

Ich schafe es einfach nicht in mathe gut zu werden und alle sagen mathe könnte jeder wenn er lernt, aber bei mir geht es einfach nicht.

Ich werde jetzt die sommerferien die heute bei mir begonnen haben erneut viel Mathe lernen aber das wird warschenlich auch nichs bringen

Guten Morgen!

Ich rechne gerade ein paar alte Aufgaben durch und komme bei folgender nicht weiter:

Woher weiß man, wie man die Funktion verändern muss, wenn man Punkte bzw Eigenschaften hat, denen man die Funktion anpassen soll, wenn man nicht genau weiß wie sie aussieht

Viele Grüße und danke im voraus!