Hallo,

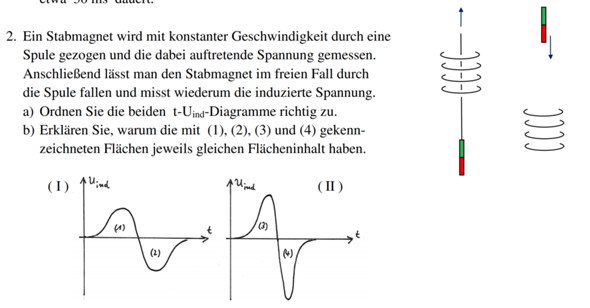
sei f: X-->Y und g: Y-->Z und dementsprechend g°f : X --> Z.

Ich versuche folgendes zu zeigen: g°f und f injektiv => g injektiv

Mir sind die Definitionen von Injektivität und Surjektivität klar. Hier habe ich allerdings ein Problem.

Ich möchte ja für alle a,b in Y zeigen, dass aus g(a)=g(b) folgt, dass a=b.

wenn ich nun f(g(a))=f(g(b)) betrachte, so ist das ja f°g und ich kann die Injektivität von g°f nicht gewinnbringend nutzen.

Auch kann man nicht sagen, dass u,v in X exisitieren, so dass a=f(u) und b=g(v) und dann mit g(f(u))=g(f(v)) arbeiten, weil man leider nicht weiß, ob f surjektiv ist.

Kann mir wer helfen?

Kann es ein Polynom geben, deren Ableitung und es selbst keine Nullstellen haben?

Zur a): Ich würde sagen, dass (II) zum freien Fall gehört, aber auch nur, weil (I) etwas zu ideal für den freien Fall aussieht - wie formuliert man das physikalisch korrekt?

Zur b) Hier kann ich leider nichts konkret sagen, das Integral von t_1 bis t_2 über den Induktionsstrom ist gleich -N·ΔΦ. Es ist für mich auch intuitiv sehr logisch, dass die gesamte Induktionsspannung, die induziert wurde, am Ende wieder ausgeglichen wird. Aber auch hier fehlt mir eine physikalischere Begründung.

Hallo,

folgende Aufgabe:

Ich habe so etwas ähnliches bereits beim Millikan-Versuch und der Braunschen Röhre gehabt, allerdings weiß ich hier nicht ganz, wie ich damit umgehen soll.

Ich habe zunächst ein Koordinantensystem eingezeichnet, die Geschwindigkeit in y-Richtung ist v_y=gt und in x-Richtung v_x=(Eq)/m·t

Ich stehe gerade ein wenig auf dem Schlauch, kann mir jemand helfen. Es handelt sich hier um eine parabelförmige Bahn, auf das Tröpfchen wirkt die Gewichtskraft und die elektrische Kraft.

Hallo,

ich habe ein Fadenpendel der Länge l=60m, an dessen Ende eine Bleikugel mit m=30kg hängt. Das Fadenpendel wird in horizontaler Richtung um 2m ausgelenkt. Gesucht ist die maximale Geschwindigkeit.

Ich kann doch y(t)=2m*cos(sqrt(g/l)*t) ableiten, so dass ich v(t)=-2m*sqrt(g/l)*sin(sqrt(g/l)*t) habe, wenn das maximal werden soll, ist |v(t)|<=2m*sqrt(g/l), also v_max=2m*sqrt(9.81m/s²/60m)=0.8087 m/s.

Über einen Energieansatz erhalte ich allerdings etwas anderes - was sagt ihr?

Fällt ein Stabmagnet mit dem Südpol nach vorne durch eine Spule, ergibt sich folgendes U-t-Diagramm. Wie lässt begründen diese Kurve begründen? (Elektromagnetische Induktion)

Ich weiß, dass der induzierte Strom am Anfang am größten ist und immer weiter abnimmt je mehr der Stabmagnet von der Spule umgeben ist. Wenn er wieder unten rausfällt, ist die Spannung nochmal hoch, weil dann nur der Nordpol am Spulenende noch innerhalb der Spule ist.

Ich habe mir überlegt, warum der Graph abnimmt und wann er genau =0 ist.

Folgende Skizze:

Wenn der Stabmagnet volländig in die Sule eingetaucht ist, wird jeweils eine "Spulenfläche" von magnetischen Feldlinien durchsetzt, aber in umgekehrter Richtung, d. h. auch der Strom läuft jeweils die Gegenrichtung, so dass er sich wechselseitig aufhebt?

Die Lösung soll K(4|6,4|1,4) sein. Ich habe was anderes. Was ist falsch an meiner Vorgehensweise?

Ich habe F(4|4|2), G(0|4|2) und H(0|0|3) abgelesen und die Ebene durch diese drei Punkte bestimmt, also E: y+4z=12. Dann habe ich den Winkel zwischen E und der Ebene F : z=2 mit 14.04 Grad errechnet. Die Idee:

Den Neigungswinkel habe ich bestimmt, danach habe ich die Gleichung aufgestellt: tan(14.04)=x/0.6 => x=0.15

Also insgesamt K(4|4+0.15|1.4)

Wo ist der Fehler?

Neon-Atom: Schalenmodell

Termschema:

Warum ist in dem Termschema von drei Energieniveaus die Rede, wenn es doch nur 2 Schalen gibt?

Ein Doppelspalt mit dem Mittenabstand von 0.8mm wird mit einfarbigem Licht von einer weit entfernten Punktquelle beleuchtet. Auf einem vom Doppelspalt 50 cm entfernten Schirm ein Interferenzmuster.

a) Der Abstand zwischen zwei benachbarten dunklen Interferenzstreifen beträgt 0.304 mm. Berechnen Sie die Wellenlänge des Lichts.

Antwort: λ=(Abstand zweier Maxima/Minima · Mittenabstand)/(Abstand zum Schirm)

also λ=(0.304mm· 0.8mm)/500mm=464.4 Nanometer

b) Schätzen Sie den Spaltabstand ab, bei dem das 1. Maximum vom zentralen Maximum 2 mm entfernt wäre. Begründen Sie ihr ergebnis rechnerisch.

Wie macht man das rechnerisch? Pythagoras?

Hallo,

Ich denke, dass es die Kardinalität dieser Teilmenge 3 ist, denn:

Nach welcher Logik wählt WolframAlpha die Basisvektoren aus?

Hallo,

es geht um Musik

Hallo,

"XXXX est le caractère principal du texte 'XXXXX'. Dans ce qui suit, il doit être charactisé :"

Macht die Übersetzung sinn?

Bonjour!

Hier der Text, den ich gerade geschrieben habe:

"Dans le texte 'Ma mère, son mec, mes demi-frères et moi' de Anne-Sophie Erhart de l'année 2003, il s'agit des jeunes en une nouvelle famille.

Au début du texte, il donne au lecteur une idée, ce qui une "famille recomposées". D'ailleurs, il attire l'attention sur le nombre, qui sonst concernés.

D'abord, le texte raconte du circonstances familiares de Cyril. Elle dit, s'elle contente avec la nouveau famille, bien qu'elle n'ai pas sentiments pour leur beau-père.

En fin de compte, le texte parle de Emma, qui trouve que leur beau-père est un personne qui n'est pas d'ici. Elle a un compréhension different concerant la 'famille idéale'"

Hallo,

Ich zitiere:

" But today, just a few years into the twenty-first century, we've already found ourselves in a different and sometimes precarious position. As revolutions in communications and technology have broken down barriers across the world, it's given more power to both our competitors and to our enemies.

No longer can we assume that a high-school education in Boston is enough to compete for a job that can easily go to the college-educated in Bangalore or in Bejing. No more can we count on employers to provide health care and pensions and job training when their bottom lines know no borders. Never again can we expect the oceans that surround America to keep us safe from attacks on our own soil.

Was adressiert Obama in diesem Abschnitt? Oder was ist sein Besorgnis?

Wann meint man einen speziellen Donnerstag und wann "an jedem Donnerstag"?

Mit Beispielsatz wäre super!

Hallo,

Hier ist die Erklärung:

Könntet ihr vielleicht mal einen Beispielsatz für beide der Fälle bilden? Ich blicke hier nicht wirklich durch!

Hallo

Reflexive Verben sind z. B. "sich waschen". Wie verhalten sich diese im passé composé?

Hier einige Beispiele:

Ich habe mich gewaschen ---> Je me suis lavé

Er hat dich gewaschen ---> Il t'a lavé

Du hast mich gewaschen ---> Tu m'as lavé

Ich sehe hier wirklich kein großes Muster, kann mir jemand weiterhelfen?